Score-based Generative Modeling in Latent Space
News
Abstract
Score-based generative models (SGMs), also known as denoising diffusion models, have recently demonstrated impressive results in terms of both sample quality and distribution coverage. However, they are usually applied directly in data space and often require thousands of network evaluations for sampling. Here, we propose the Latent Score-based Generative Model (LSGM), a novel approach that trains SGMs in a latent space, relying on the variational autoencoder framework. Moving from data to latent space allows us to train more expressive generative models, apply SGMs to non-continuous data, and learn smoother SGMs in a smaller space, resulting in fewer network evaluations and faster sampling. To enable training LSGMs end-to-end in a scalable and stable manner, we (i) introduce a new score-matching objective suitable to the LSGM setting, (ii) propose a novel parameterization of the score function that allows SGM to focus on the mismatch of the target distribution with respect to a simple Normal one, and (iii) analytically derive multiple techniques for variance reduction of the training objective. LSGM obtains a state-of-the-art FID score of 2.10 on CIFAR-10, outperforming all existing generative results on this dataset. On CelebA-HQ-256, LSGM is on a par with previous SGMs in sample quality while outperforming them in sampling time by two orders of magnitude. In modeling binary images, LSGM achieves state-of-the-art likelihood on the binarized OMNIGLOT dataset.
Score-based Generative Modeling in Latent Space
Recently, score-based generative models (SGMs) demonstrated astonishing results in terms of both high sample quality and mode coverage. These models define a forward diffusion process that maps data to noise by gradually perturbing the input data. Generation corresponds to a reverse process that synthesizes novel data via iterative denoising, starting from random noise. The training problem then reduces to learning the score function--the gradient of the log-density--of the perturbed data.
Albeit high quality, sampling from SGMs is computationally expensive. This is because generation amounts to solving a complex SDE, or equivalently ordinary differential equation (ODE), that maps a simple base distribution to the complex data distribution. The resulting differential equations are typically complex and solving them accurately requires numerical integration with very small step sizes, which results in thousands of neural network evaluations. Furthermore, generation complexity is uniquely defined by the underlying data distribution and the forward SDE for data perturbation, implying that synthesis speed cannot be increased easily without sacrifices. Moreover, SDE-based generative models are currently defined for continuous data and cannot be applied effortlessly to binary, categorical, or graph-structured data.
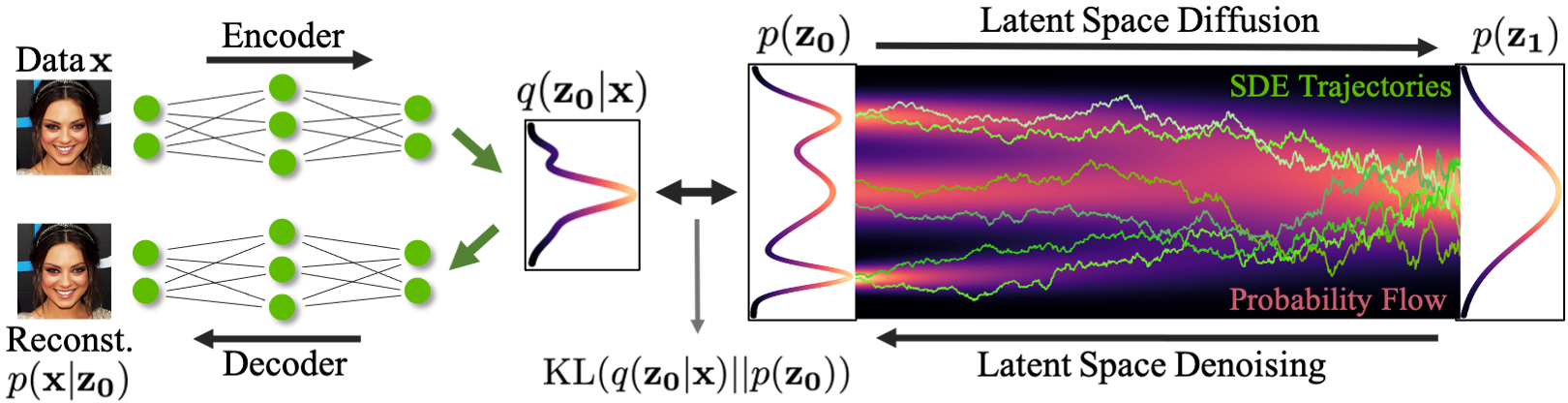
In this paper, we propose the Latent Score-based Generative Model (LSGM), a new approach for learning SGMs in latent space, leveraging a variational autoencoder (VAE) framework. We map the input data to latent space and apply the score-based generative model there. The score-based model is then tasked with modeling the distribution over the latent embeddings of the data set. Novel data synthesis is achieved by first generating embeddings via drawing from a simple base distribution followed by iterative denoising, and then transforming this embedding via a decoder to data space. We can consider this model a VAE with an SGM prior. See our figure above for additional details.
Advantages of Latent Score-based Generative Models
Synthesis Speed: By pretraining the VAE with a Normal prior first, we can bring the marginal distribution over encodings (the aggregate posterior) close to the Normal prior, which is also the SGM's base distribution. Consequently, the SGM only needs to model the remaining mismatch, resulting in a less complex model from which sampling becomes easier. Furthermore, we can tailor the latent space according to our needs. For example, we can use hierarchical latent variables and apply the diffusion model only over a subset of them or at a small resolution, further improving synthesis speed.
Expressivity: Training a regular SGM can be considered as training a neural ODE directly on the data. However, previous works found that augmenting neural ODEs and more generally generative models with latent variables improves their expressivity. Consequently, we expect similar expressivity improvements from combining SGMs with a latent variable framework.
Tailored Encoders and Decoders: Since we use the SGM in latent space, we can utilize carefully designed encoders and decoders mapping between latent and data space, further improving expressivity. Additionally, the LSGM method can therefore be naturally applied to non-continuous data.
Technical Contributions
LSGMs can be trained end-to-end by maximizing the variational lower bound on the data likelihood. Compared to regular score matching, our approach comes with additional challenges, since both the score-based denoising model and its target distribution, formed by the latent space encodings, are learnt simultaneously. To this end, we make the following technical contributions: (i) We derive a new denoising score matching objective that allows us to efficiently learn the VAE model and the latent SGM prior at the same time. (ii) We introduce a new parameterization of the latent space score function, which mixes a Normal distribution with a learnable SGM, allowing the SGM to model only the mismatch between the distribution of latent variables and the Normal prior. (iii) We propose techniques for variance reduction of the training objective by designing a new SDE and by analytically deriving importance sampling schemes, allowing us to stably train deep LSGMs.
Results
Experimentally, we achieve state-of-the-art 2.10 FID on CIFAR-10 and 7.22 FID on CelebA-HQ-256, and significantly improve upon likelihoods of previous SGMs. On CelebA-HQ-256, we outperform previous SGMs in synthesis speed by two orders of magnitude. LSGM requires 23 and 138 function evaluations on the CelebA-HQ-256 and CIFAR-10 datasets, respectively. We also model binarized images, MNIST and OMNIGLOT, achieving state-of-the-art likelihood on the latter.

Generated samples for different datasets. LSGM successfully generates sharp, high-quality, and diverse samples.
The sequence above is generated by randomly traversing in the latent space of LSGM.

We visualize the evolution of the latent variables under the reverse-time generative process by feeding latent variables from different stages along the process to the decoder to map them back to image space.
Paper
Score-based Generative Modeling in Latent Space
Arash Vahdat*, Karsten Kreis*, Jan Kautz
* Authors contributed equally.
Citation
@inproceedings{vahdat2021score,
title={Score-based Generative Modeling in Latent Space},
author={Vahdat, Arash and Kreis, Karsten and Kautz, Jan},
booktitle={Neural Information Processing Systems (NeurIPS)},
year={2021}
}