Tackling the Generative Learning Trilemma with Denoising Diffusion GANs
News
Abstract
A wide variety of deep generative models has been developed in the past decade. Yet, these models often struggle with simultaneously addressing three key requirements including: high sample quality, mode coverage, and fast sampling. We call the challenge imposed by these requirements the generative learning trilemma, as the existing models often trade some of them for others. Particularly, denoising diffusion models have shown impressive sample quality and diversity, but their expensive sampling does not yet allow them to be applied in many real-world applications. In this paper, we argue that slow sampling in these models is fundamentally attributed to the Gaussian assumption in the denoising step which is justified only for small step sizes. To enable denoising with large steps, and hence, to reduce the total number of denoising steps, we propose to model the denoising distribution using a complex multimodal distribution. We introduce denoising diffusion generative adversarial networks (denoising diffusion GANs) that model each denoising step using a multimodal conditional GAN. Through extensive evaluations, we show that denoising diffusion GANs obtain sample quality and diversity competitive with original diffusion models while being 2000× faster on the CIFAR-10 dataset. Compared to traditional GANs, our model exhibits better mode coverage and sample diversity. To the best of our knowledge, denoising diffusion GAN is the first model that reduces sampling cost in diffusion models to an extent that allows them to be applied to real-world applications inexpensively.
The Generative Learning Trilemma
In the past decade, a plethora of deep generative models has been developed for various domains such as images, audio, point clouds and graphs. However, current generative learning frameworks cannot yet simultaneously satisfy three key requirements, often needed for their wide adoption in real-world problems. These requirements include (i) high-quality sampling, (ii) mode coverage and sample diversity, and (iii) fast and computationally inexpensive sampling. For example, most current works in image synthesis focus on high-quality generation. However, mode coverage and data diversity are important for better representing minorities and for reducing the negative social impacts of generative models. Additionally, applications such as interactive image editing or real-time speech synthesis require fast sampling. Here, we identify the challenge posed by these requirements as the generative learning trilemma, since existing models usually compromise between them.

The figure above summarizes how mainstream generative frameworks tackle the trilemma. Generative adversarial networks (GANs) generate high-quality samples rapidly, but they are known for poor mode coverage. Conversely, variational autoencoders (VAEs) and normalizing flows cover data modes faithfully, but they often suffer from low sample quality. Recently, diffusion models have emerged as powerful generative models. These models demonstrate surprisingly good results in sample quality, beating GANs in image generation. They also feature good mode coverage and sample diversity, indicated by high likelihood. Diffusion models have already been applied to a variety of generation tasks. However, sampling from them often requires thousands of neural network evaluations, making their application to real-world problems expensive. In this paper, we tackle the generative learning trilemma by reformulating denoising diffusion models specifically for fast sampling while maintaining strong mode coverage and sample quality.
Why is Sampling from Denoising Diffusion Models so Slow?
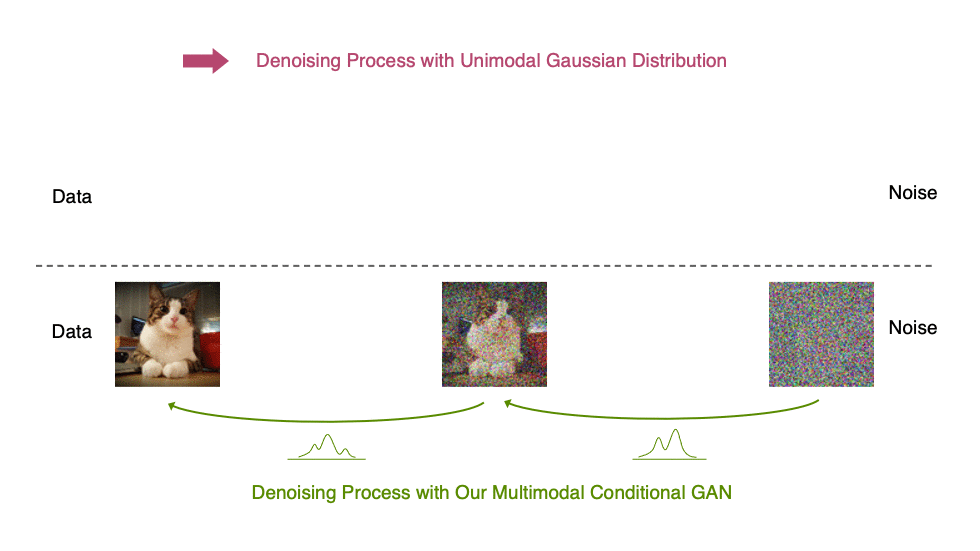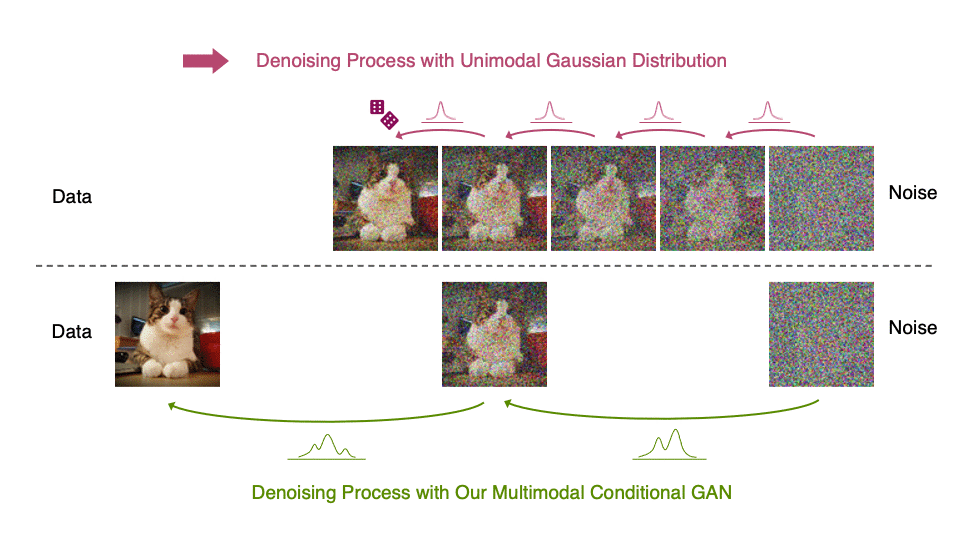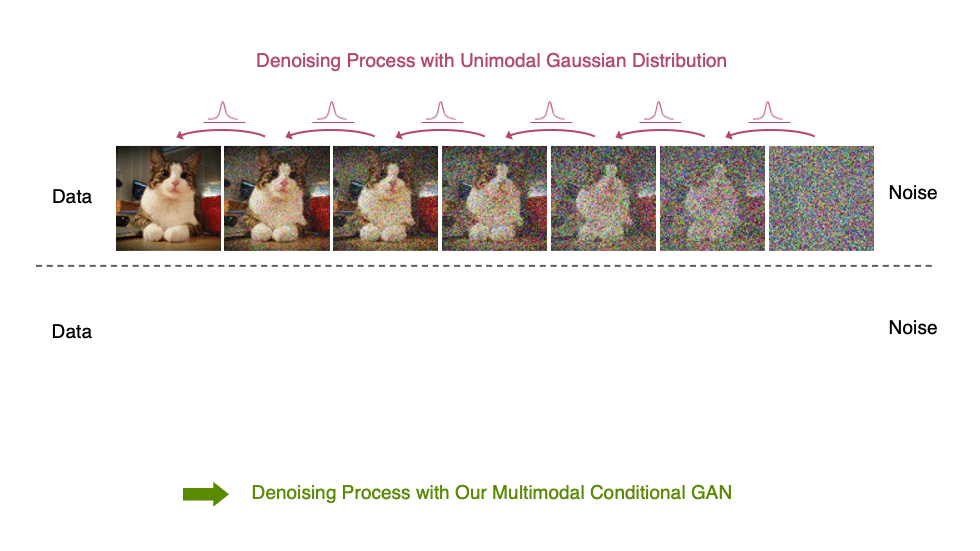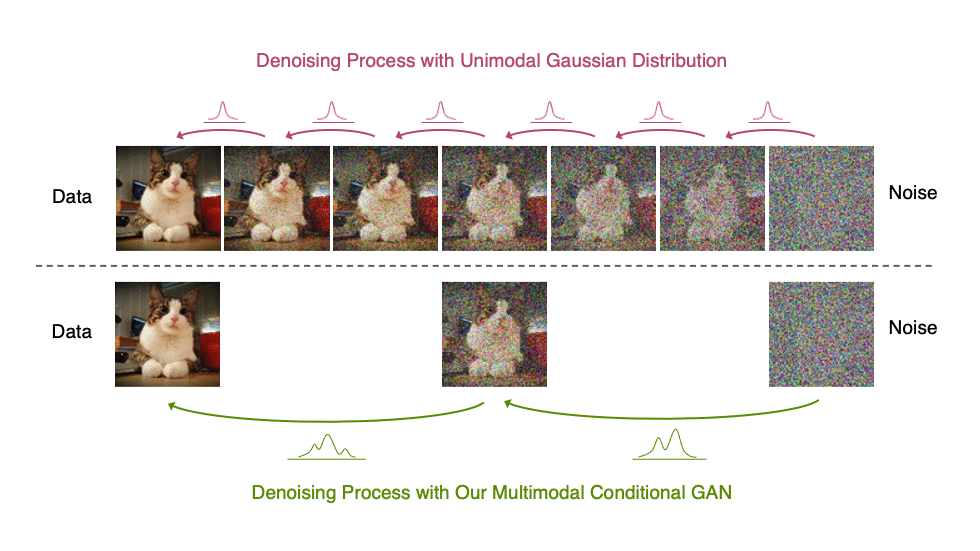
Diffusion models define a forward diffusion process that maps data to noise by gradually perturbing the input data. Data generation is achieved using a parametrized reverse process that performs iterative denoising in thousands of steps, starting from random noise. In this paper, we investigate the slow sampling issue of diffusion models and we observe that diffusion models commonly assume that the denoising distribution in the reverse can be approximated by Gaussian distributions. However, it is known that the Gaussian assumption holds only in the infinitesimal limit of small denoising steps, which leads to the requirement of a large number of steps in the reverse process. When the reverse process uses larger step sizes (i.e., it has fewer denoising steps), we need a non-Gaussian multimodal distribution for modeling the denoising distribution. Intuitively, in image synthesis, the multimodal distribution arises from the fact that multiple plausible clean images may correspond to the same noisy image.
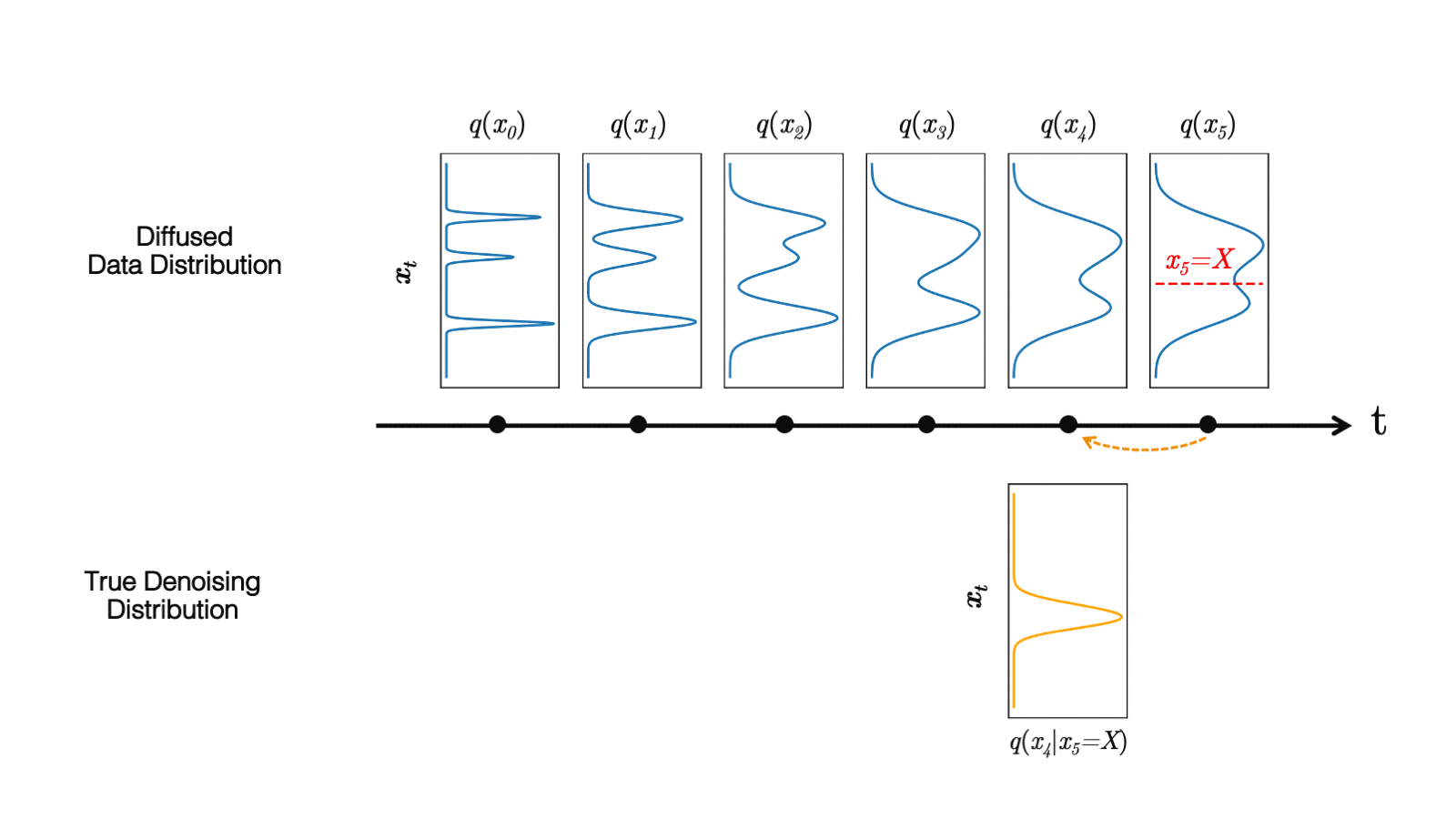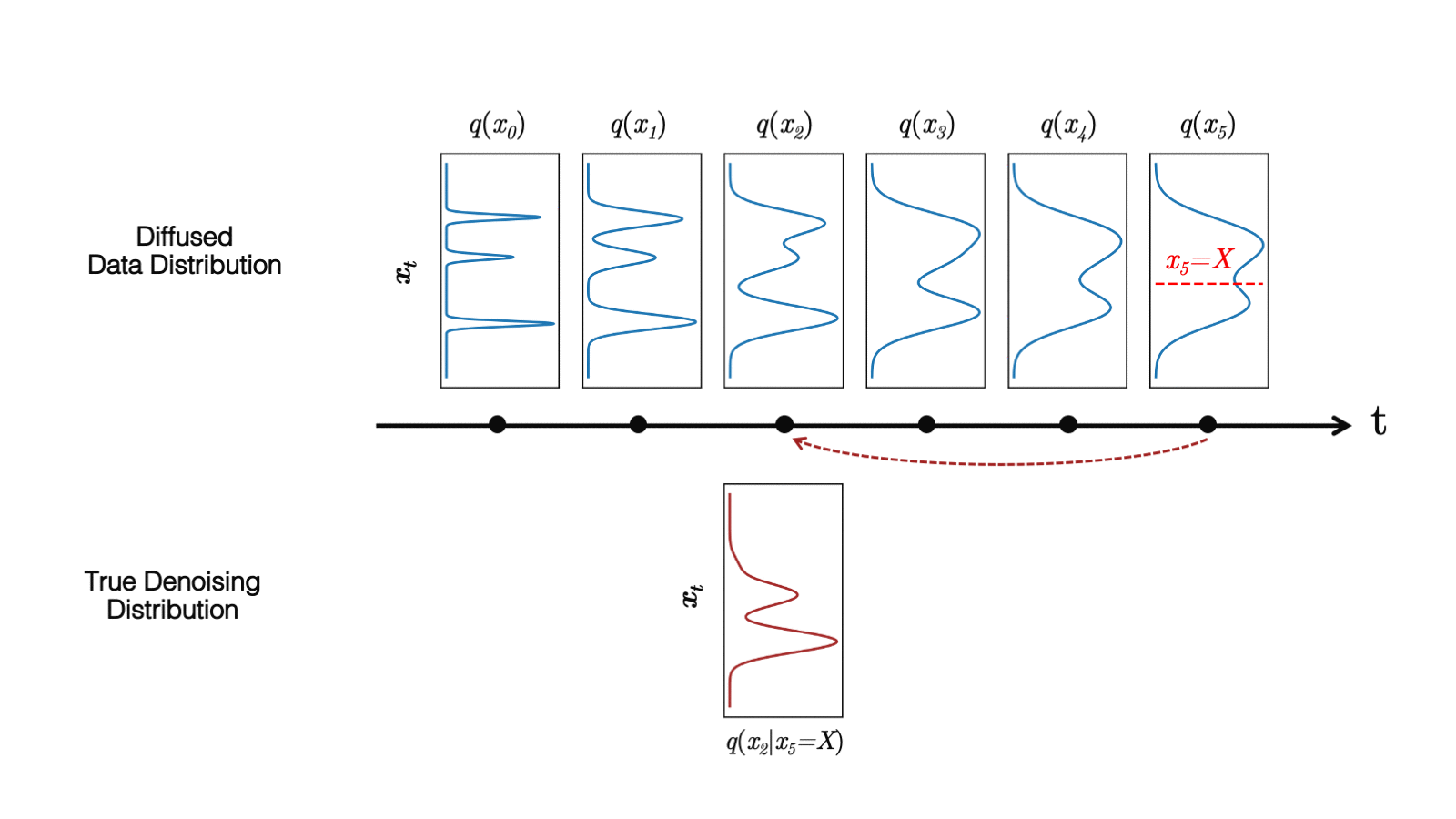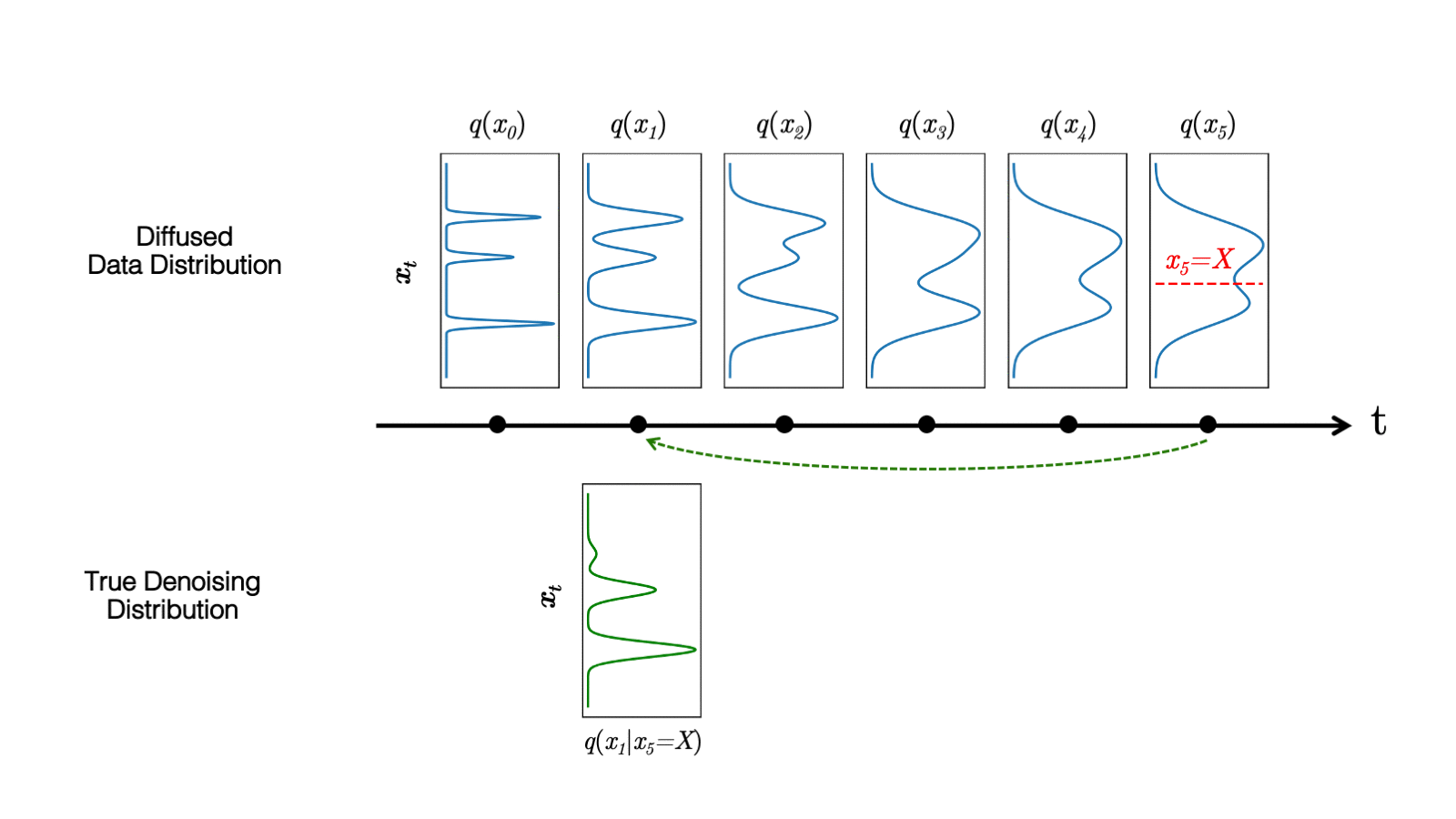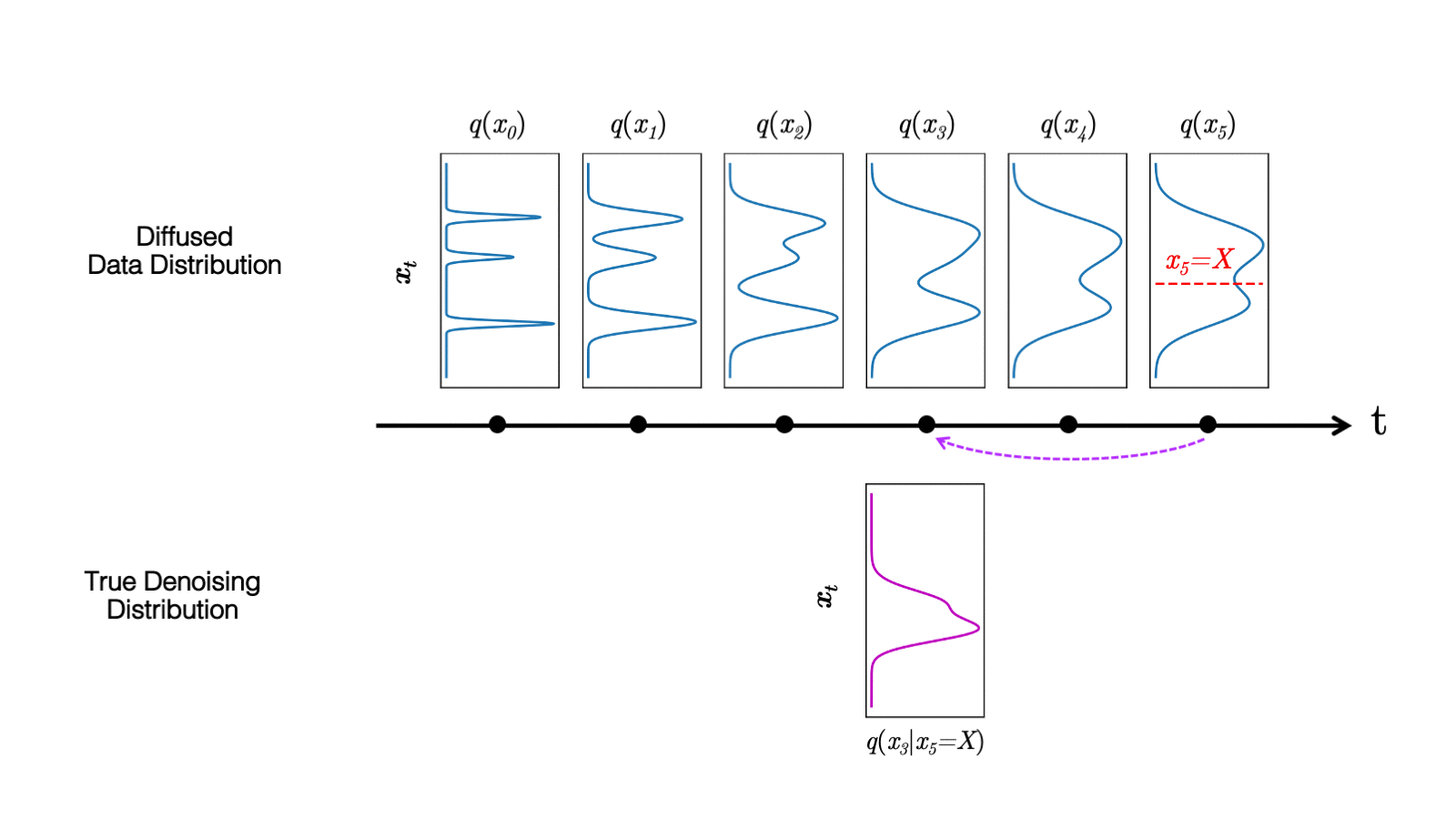
Top: Evolution of a 1D data distribution q(x0) according to the forward diffusion process. Bottom: Visualizations of the true denoising distribution when conditioning on a fixed x5 with varying step sizes shown in different colors. The true denoising distribution for a small step size (shown in yellow) is close to a Gaussian distribution. However, it becomes more complex and multimodal as the step size increases.
Denoising Diffusion GANs
Inspired by the observation above, we propose to parametrize the denoising distribution with an expressive multimodal distribution to enable denoising with large steps. In particular, we introduce a novel generative model, termed as denoising diffusion GAN, in which the denoising distributions are modeled with conditional GANs.
Our adversarial training setup is shown below. Given a training image x0, we use the forward Gaussian diffusion process to sample from xt-1 and xt, the diffused samples at two successive steps. Given xt, our conditional denoising GAN first stochastically generates x'0 and then uses the tractable posterior distribution q(xt-1|xt, x0) to generate x't-1. The discriminator is trained to distinguish between the real (xt-1, xt) vs. fake (x't-1, xt) pairs. We train both generator and discriminator using the non-saturated GAN objective simultaneously for all time steps t. Generators and discriminators for different steps t share parameters, while additionally conditioning on t-embeddings, similar to regular denoising diffusion models.
After training, we generate novel instances by sampling from noise and iteratively denoising it in a few steps using our denoising diffusion GAN generator.

The training process of denoising diffusion GAN. We train a conditional GAN generator to denoise input xt using an adversarial loss for different steps in the diffusion process.
Advantages over Traditional GANs
One natural question for our model is, why not just train a GAN that can generate samples in one shot using a traditional setup, in contrast to our model that iteratively generates samples by denoising? Our model has several advantages over traditional GANs: GANs are known to suffer from training instability and mode collapse, and some possible reasons include the difficulty of directly generating samples from a complex distribution in one-shot, and the overfitting issue when the discriminator only looks at clean samples. In contrast, our model breaks the generation process into several conditional denoising diffusion steps in which each step is relatively simple to model, due to the strong conditioning on xt. Moreover, the diffusion process smoothens the data distribution, making the discriminator less likely to overfit. Thus, we observe that our model exhibits better training stability and mode coverage.
Results
In image generation, we observe that our model achieves sample quality and mode coverage competitive with diffusion models, while requiring only as few as two denoising steps, achieving up to 2,000× speed-up in sampling compared to predictor-corrector sampling on CIFAR-10. Compared to traditional GANs, we show that our model significantly outperforms state-of-the-art GANs in sample diversity, while being competitive in sample fidelity.
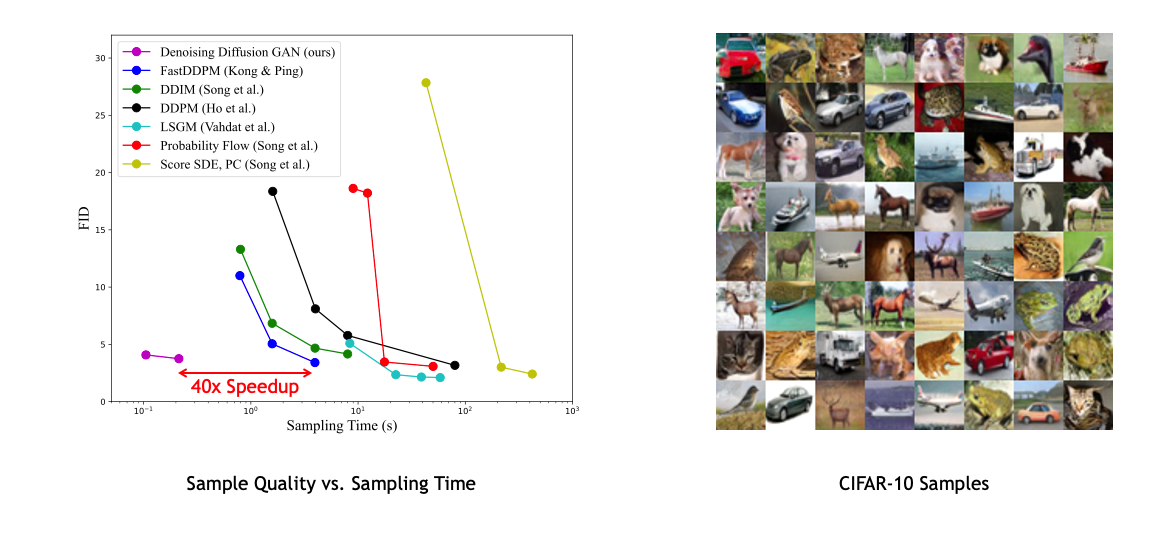
Left: Sample quality vs. sampling time is shown for different diffusion-based generative models for the CIFAR-10 image modeling benchmark. Denoising diffusion GAN achieves a speedup of several orders of magnitude compared to previous diffusion models while maintaining similar synthesis quality. Right: Generated CIFAR-10 samples.

Qualitative results on CelebA-HQ 256 (left) and LSUN Church Outdoor 256 (right).
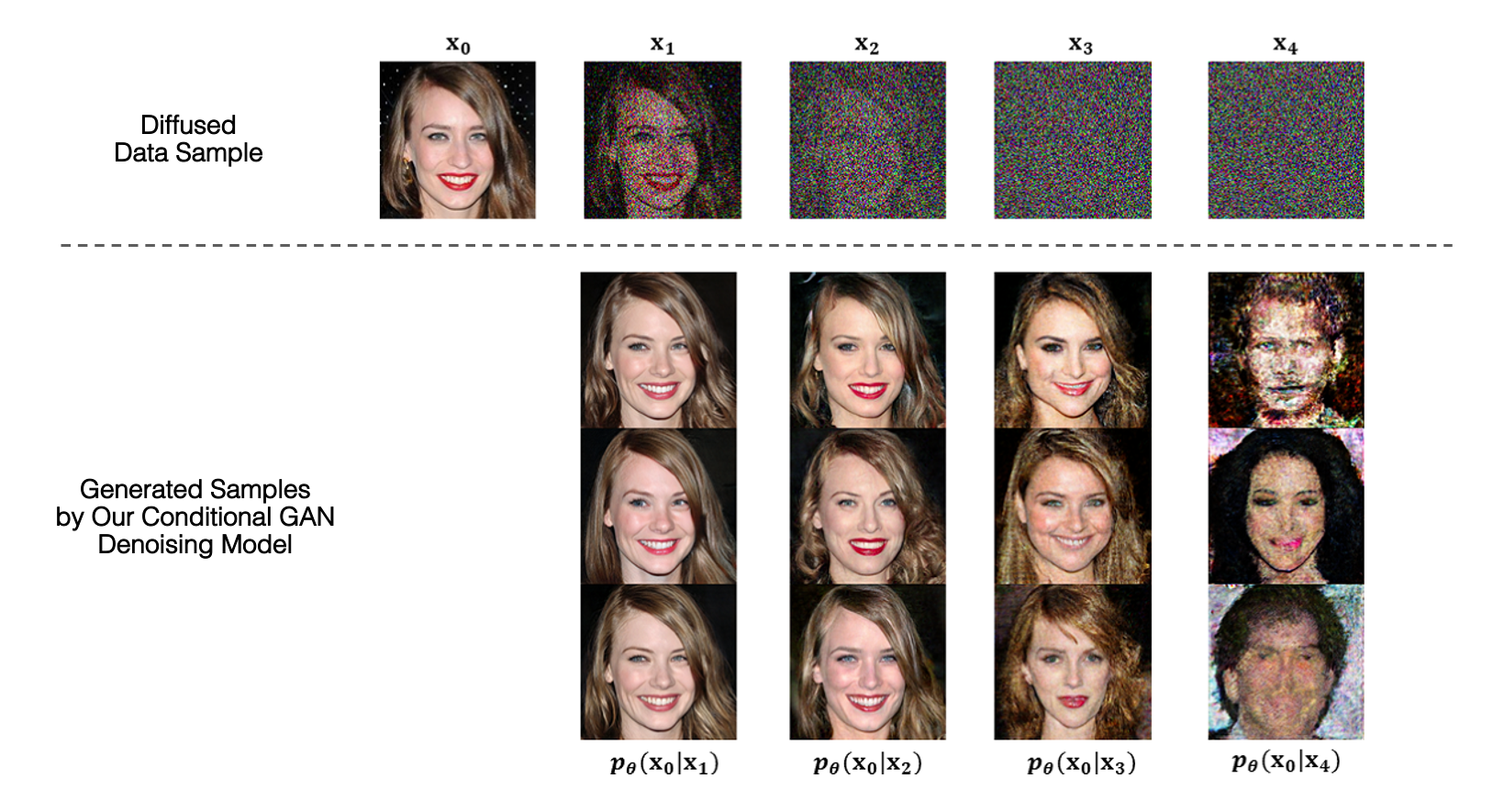
Top: Visualization of a training sample x0 at different steps of the forward diffusion process. Bottom: Each column visualizes 3 samples generated by our conditional GAN denoising model pθ(x0|xt) conditioned on the diffused sample at step t.
Paper
Tackling the Generative Learning Trilemma with Denoising Diffusion GANs
Zhisheng Xiao*, Karsten Kreis, Arash Vahdat
* Work done during an internship at NVIDIA.
Citation
@inproceedings{xiao2022DDGAN,
title={Tackling the Generative Learning Trilemma with Denoising Diffusion {GAN}s},
author={Zhisheng Xiao and Karsten Kreis and Arash Vahdat},
booktitle={International Conference on Learning Representations (ICLR)},
year={2022}
}