Appendix C Closed-Form Solution for First-Order Diffraction

For first-order diffraction, the position of the diffraction point can be determined in closed form. Consider a source $\mathbf{s}$ , a target $\mathbf{t}$ , and an edge defined by its direction $\widehat{\mathbf{e}}$ . For convenience, we assume the edge passes through the origin of the coordinate system, denoted by $\mathbf{o}$ .

According to Fermat’s principle, the diffraction point $\mathbf{v}$ on the edge minimizes the total path length $\mathbf{s}\rightarrow\mathbf{v}\rightarrow\mathbf{t}$ . This corresponds to minimizing the function

{\cal L}\left(x\right)=\left\lVert\mathbf{s}-\mathbf{v}\right\rVert_{2}+\left% \lVert\mathbf{v}-\mathbf{t}\right\rVert_{2}

(183)

where

\mathbf{v}=x\widehat{\mathbf{e}}.

(184)

As shown in [22], ${\cal L}\left(\cdot\right)$ is strictly convex and thus has a unique minimizer.

We introduce the set of vectors $\left(\widehat{\mathbf{u}}_{1},\widehat{\mathbf{u}}_{2},\widehat{\mathbf{u}}_{% 3}\right)$ , where

$\displaystyle\widehat{\mathbf{u}}_{1}$	$\displaystyle=\frac{\mathbf{s}-\left(\widehat{\mathbf{e}}^{\mathsf{T}}\mathbf{% s}\right)\widehat{\mathbf{e}}}{\left\lVert\mathbf{s}-\left(\widehat{\mathbf{e}% }^{\mathsf{T}}\mathbf{s}\right)\widehat{\mathbf{e}}\right\rVert_{2}}$	(185)
$\displaystyle\widehat{\mathbf{u}}_{2}$	$\displaystyle=\frac{\mathbf{t}-\left(\widehat{\mathbf{e}}^{\mathsf{T}}\mathbf{% s}\right)\widehat{\mathbf{e}}}{\left\lVert\mathbf{t}-\left(\widehat{\mathbf{e}% }^{\mathsf{T}}\mathbf{s}\right)\widehat{\mathbf{e}}\right\rVert_{2}}$	(186)
$\displaystyle\widehat{\mathbf{u}}_{3}$	$\displaystyle=\begin{cases}\widehat{\mathbf{u}}_{1}\times\widehat{\mathbf{u}}_% {2}&\text{ if }\widehat{\mathbf{u}}_{1}\times\widehat{\mathbf{u}}_{2}\neq% \mathbf{0}\\ \widehat{\mathbf{e}}&\text{ if }\widehat{\mathbf{u}}_{1}\times\widehat{\mathbf% {u}}_{2}=\mathbf{0}\end{cases}.$	(187)

Note that $\widehat{\mathbf{u}}_{3}=\pm\widehat{\mathbf{e}}$ , and that the source and the edge lie within the plane $\left(\mathbf{o},\widehat{\mathbf{u}}_{1},\widehat{\mathbf{e}}\right)$ . A key observation is that rotating the target $\mathbf{t}$ about the edge does not alter the path length. Specifically, let $\mathbf{R}_{\widehat{\mathbf{u}}_{3}}\left(\phi\right)$ denote the rotation matrix for an angle $\phi$ around the edge $\left(\mathbf{o},\widehat{\mathbf{e}}\right)$ . Then,

	$\displaystyle{\cal L}\left(x\right)$	$\displaystyle=\left\lVert\mathbf{s}-\mathbf{v}\right\rVert_{2}+\left\lVert% \mathbf{v}-\mathbf{t}\right\rVert_{2}$		(188)
		$\displaystyle=\left\lVert\mathbf{s}-\mathbf{v}\right\rVert_{2}+\lVert\mathbf{v% }-\underbrace{\mathbf{R}_{\widehat{\mathbf{u}}_{3}}\left(\phi\right)\mathbf{t}% }_{\mathbf{t}^{\prime}}\rVert_{2}$		(189)

holds for any $\phi\in\mathbb{R}$ . Especially, by rotating the target around the axis ( $\mathbf{o},\widehat{\mathbf{u}}_{3}$ ) by the angle

\phi=\pi-\arccos\left(\widehat{\mathbf{u}}_{1}^{\mathsf{T}}\widehat{\mathbf{u}% }_{2}\right),

(191)

the rotated target $\mathbf{t}^{\prime}$ is placed in the same plane $\left(\mathbf{o},\widehat{\mathbf{u}}_{1},\widehat{\mathbf{e}}\right)$ as the source and the edge, but on the side opposite to the source with respect to the edge, as depicted in Figure 36. The rotation matrix $\mathbf{R}_{\widehat{\mathbf{u}}_{3}}\left(\phi\right)$ is given by Rodrigues’ rotation formula [30].

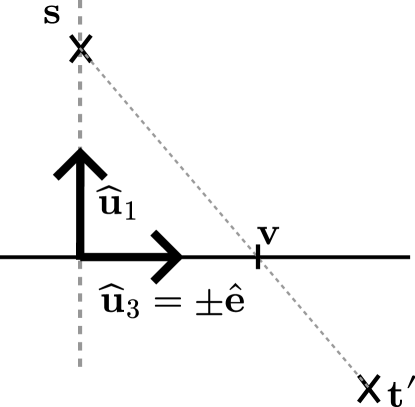
Refer to caption — (a) View in the plane $\left(\mathbf{o},\widehat{\mathbf{u}}_{1},\widehat{\mathbf{u}}_{2}\right)$ , which is perpendicular to the edge $\widehat{\mathbf{e}}$ .

Minimizing ${\cal L}\left(x\right)$ with the rotated target $\mathbf{t}^{\prime}$ is equivalent to $\mathbf{s}$ , $\mathbf{v}$ , and $\mathbf{t}^{\prime}$ being collinear, i.e.

	$\displaystyle(\mathbf{v}-\mathbf{s})\times\overrightarrow{\mathbf{s}\mathbf{t}% ^{\prime}}$	$\displaystyle=\mathbf{0}$		(192)
	$\displaystyle\Leftrightarrow\quad x\left(\widehat{\mathbf{e}}\times% \overrightarrow{\mathbf{s}\mathbf{t}^{\prime}}\right)$	$\displaystyle=\mathbf{s}\times\overrightarrow{\mathbf{s}\mathbf{t}^{\prime}}$		(193)

where $\overrightarrow{\mathbf{s}\mathbf{t}^{\prime}}=\mathbf{t}^{\prime}-\mathbf{s}$ . Since $\widehat{\mathbf{e}}\times\overrightarrow{\mathbf{s}\mathbf{t}^{\prime}}$ and $\mathbf{s}\times\overrightarrow{\mathbf{s}\mathbf{t}^{\prime}}$ are parallel, the solution for $x$ is

x=\operatorname{sign}\left(\left[\widehat{\mathbf{e}}\times\overrightarrow{% \mathbf{s}\mathbf{t}^{\prime}}\right]^{\mathsf{T}}\left[\mathbf{s}\times% \overrightarrow{\mathbf{s}\mathbf{t}^{\prime}}\right]\right)\frac{\left\lVert% \mathbf{s}\times\overrightarrow{\mathbf{s}\mathbf{t}^{\prime}}\right\rVert_{2}% }{\left\lVert\widehat{\mathbf{e}}\times\overrightarrow{\mathbf{s}\mathbf{t}^{% \prime}}\right\rVert_{2}}.

(194)

NVIDIA Sionna RT

Appendix C Closed-Form Solution for First-Order Diffraction