Low-Density Parity-Check (LDPC)
The low-density parity-check (LDPC) code module supports 5G compliant LDPC codes and allows iterative belief propagation (BP) decoding. Further, the module supports rate-matching for 5G and provides a generic linear encoder.
The following code snippets show how to setup and run a rate-matched 5G compliant LDPC encoder and a corresponding belief propagation (BP) decoder.
First, we need to create instances of LDPC5GEncoder and LDPC5GDecoder:
encoder = LDPC5GEncoder(k = 100, # number of information bits (input)
n = 200) # number of codeword bits (output)
decoder = LDPC5GDecoder(encoder = encoder,
num_iter = 20, # number of BP iterations
return_infobits = True)
Now, the encoder and decoder can be used by:
# --- encoder ---
# u contains the information bits to be encoded and has shape [...,k].
# c contains the polar encoded codewords and has shape [...,n].
c = encoder(u)
# --- decoder ---
# llr contains the log-likelihood ratios from the demapper and has shape [...,n].
# u_hat contains the estimated information bits and has shape [...,k].
u_hat = decoder(llr)
LDPC Encoder
LDPC5GEncoder
- class sionna.fec.ldpc.encoding.LDPC5GEncoder(k, n, num_bits_per_symbol=None, dtype=tf.float32, **kwargs)[source]
5G NR LDPC Encoder following the 3GPP NR Initiative [3GPPTS38212_LDPC] including rate-matching.
The class inherits from the Keras layer class and can be used as layer in a Keras model.
- Parameters:
k (int) – Defining the number of information bit per codeword.
n (int) – Defining the desired codeword length.
num_bits_per_symbol (int or None) – Defining the number of bits per QAM symbol. If this parameter is explicitly provided, the codeword will be interleaved after rate-matching as specified in Sec. 5.4.2.2 in [3GPPTS38212_LDPC].
dtype (tf.DType) – Defaults to tf.float32. Defines the output datatype of the layer (internal precision remains tf.uint8).
- Input:
inputs ([…,k], tf.float32) – 2+D tensor containing the information bits to be encoded.
- Output:
[…,n], tf.float32 – 2+D tensor of same shape as inputs besides last dimension has changed to n containing the encoded codeword bits.
- Attributes:
k (int) – Defining the number of information bit per codeword.
n (int) – Defining the desired codeword length.
coderate (float) – Defining the coderate r=
k/n.n_ldpc (int) – An integer defining the total codeword length (before punturing) of the lifted parity-check matrix.
k_ldpc (int) – An integer defining the total information bit length (before zero removal) of the lifted parity-check matrix. Gap to
kmust be filled with so-called filler bits.num_bits_per_symbol (int or None.) – Defining the number of bits per QAM symbol. If this parameter is explicitly provided, the codeword will be interleaved after rate-matching as specified in Sec. 5.4.2.2 in [3GPPTS38212_LDPC].
out_int ([n], ndarray of int) – Defining the rate-matching output interleaver sequence.
out_int_inv ([n], ndarray of int) – Defining the inverse rate-matching output interleaver sequence.
_check_input (bool) – A boolean that indicates whether the input vector during call of the layer should be checked for consistency (i.e., binary).
_bg (str) – Denoting the selected basegraph (either bg1 or bg2).
_z (int) – Denoting the lifting factor.
_i_ls (int) – Defining which version of the basegraph to load. Can take values between 0 and 7.
_k_b (int) – Defining the number of information bit columns in the basegraph. Determined by the code design procedure in [3GPPTS38212_LDPC].
_bm (ndarray) – An ndarray defining the basegraph.
_pcm (sp.sparse.csr_matrix) – A sparse matrix of shape [k_ldpc-n_ldpc, n_ldpc] containing the sparse parity-check matrix.
- Raises:
AssertionError – If
kis not int.AssertionError – If
nis not int.ValueError – If
code_lengthis not supported.ValueError – If dtype is not supported.
ValueError – If
inputscontains other values than 0 or 1.InvalidArgumentError – When rank(
inputs)<2.InvalidArgumentError – When shape of last dim is not
k.
Note
As specified in [3GPPTS38212_LDPC], the encoder also performs puncturing and shortening. Thus, the corresponding decoder needs to invert these operations, i.e., must be compatible with the 5G encoding scheme.
- property coderate
Coderate of the LDPC code after rate-matching.
- generate_out_int(n, num_bits_per_symbol)[source]
“Generates LDPC output interleaver sequence as defined in Sec 5.4.2.2 in [3GPPTS38212_LDPC].
- Parameters:
n (int) – Desired output sequence length.
num_bits_per_symbol (int) – Number of symbols per QAM symbol, i.e., the modulation order.
- Output:
(perm_seq, perm_seq_inv) – Tuple:
perm_seq (ndarray of length n) – Containing the permuted indices.
perm_seq_inv (ndarray of length n) – Containing the inverse permuted indices.
Note
The interleaver pattern depends on the modulation order and helps to reduce dependencies in bit-interleaved coded modulation (BICM) schemes.
- property k
Number of input information bits.
- property k_ldpc
Number of LDPC information bits after rate-matching.
- property n
Number of output codeword bits.
- property n_ldpc
Number of LDPC codeword bits before rate-matching.
- property num_bits_per_symbol
Modulation order used for the rate-matching output interleaver.
- property out_int
Output interleaver sequence as defined in 5.4.2.2.
- property out_int_inv
Inverse output interleaver sequence as defined in 5.4.2.2.
- property pcm
Parity-check matrix for given code parameters.
- property z
Lifting factor of the basegraph.
LDPC Decoder
LDPCBPDecoder
- class sionna.fec.ldpc.decoding.LDPCBPDecoder(pcm, trainable=False, cn_type='boxplus-phi', hard_out=True, track_exit=False, num_iter=20, stateful=False, output_dtype=tf.float32, **kwargs)[source]
Iterative belief propagation decoder for low-density parity-check (LDPC) codes and other codes on graphs.
This class defines a generic belief propagation decoder for decoding with arbitrary parity-check matrices. It can be used to iteratively estimate/recover the transmitted codeword (or information bits) based on the LLR-values of the received noisy codeword observation.
The decoder implements the flooding SPA algorithm [Ryan], i.e., all nodes are updated in a parallel fashion. Different check node update functions are available
boxplus
\[y_{j \to i} = 2 \operatorname{tanh}^{-1} \left( \prod_{i' \in \mathcal{N}_(j) \setminus i} \operatorname{tanh} \left( \frac{x_{i' \to j}}{2} \right) \right)\]boxplus-phi
\[y_{j \to i} = \alpha_{j \to i} \cdot \phi \left( \sum_{i' \in \mathcal{N}_(j) \setminus i} \phi \left( |x_{i' \to j}|\right) \right)\]with \(\phi(x)=-\operatorname{log}(\operatorname{tanh} \left(\frac{x}{2}) \right)\)
minsum
\[\qquad y_{j \to i} = \alpha_{j \to i} \cdot {min}_{i' \in \mathcal{N}_(j) \setminus i} \left(|x_{i' \to j}|\right)\]
where \(y_{j \to i}\) denotes the message from check node (CN) j to variable node (VN) i and \(x_{i \to j}\) from VN i to CN j, respectively. Further, \(\mathcal{N}_(j)\) denotes all indices of connected VNs to CN j and
\[\alpha_{j \to i} = \prod_{i' \in \mathcal{N}_(j) \setminus i} \operatorname{sign}(x_{i' \to j})\]is the sign of the outgoing message. For further details we refer to [Ryan].
Note that for full 5G 3GPP NR compatibility, the correct puncturing and shortening patterns must be applied (cf. [Richardson] for details), this can be done by
LDPC5GEncoderandLDPC5GDecoder, respectively.If required, the decoder can be made trainable and is fully differentiable by following the concept of weighted BP [Nachmani] as shown in Fig. 1 leading to
\[y_{j \to i} = 2 \operatorname{tanh}^{-1} \left( \prod_{i' \in \mathcal{N}_(j) \setminus i} \operatorname{tanh} \left( \frac{\textcolor{red}{w_{i' \to j}} \cdot x_{i' \to j}}{2} \right) \right)\]where \(w_{i \to j}\) denotes the trainable weight of message \(x_{i \to j}\). Please note that the training of some check node types may be not supported.
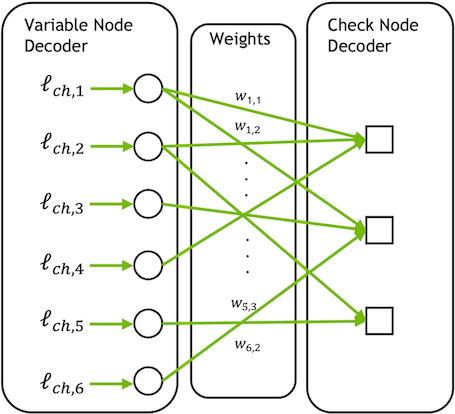
Fig. 8 Fig. 1: Weighted BP as proposed in [Nachmani].
For numerical stability, the decoder applies LLR clipping of +/- 20 to the input LLRs.
The class inherits from the Keras layer class and can be used as layer in a Keras model.
- Parameters:
pcm (ndarray) – An ndarray of shape [n-k, n] defining the parity-check matrix consisting only of 0 or 1 entries. Can be also of type scipy. sparse.csr_matrix or scipy.sparse.csc_matrix.
trainable (bool) – Defaults to False. If True, every outgoing variable node message is scaled with a trainable scalar.
cn_type (str) – A string defaults to ‘“boxplus-phi”’. One of {“boxplus”, “boxplus-phi”, “minsum”} where ‘“boxplus”’ implements the single-parity-check APP decoding rule. ‘“boxplus-phi”’ implements the numerical more stable version of boxplus [Ryan]. ‘“minsum”’ implements the min-approximation of the CN update rule [Ryan].
hard_out (bool) – Defaults to True. If True, the decoder provides hard-decided codeword bits instead of soft-values.
track_exit (bool) – Defaults to False. If True, the decoder tracks EXIT characteristics. Note that this requires the all-zero CW as input.
num_iter (int) – Defining the number of decoder iteration (no early stopping used at the moment!).
stateful (bool) – Defaults to False. If True, the internal VN messages
msg_vnfrom the last decoding iteration are returned, andmsg_vnor None needs to be given as a second input when calling the decoder. This is required for iterative demapping and decoding.output_dtype (tf.DType) – Defaults to tf.float32. Defines the output datatype of the layer (internal precision remains tf.float32).
- Input:
llrs_ch or (llrs_ch, msg_vn) – Tensor or Tuple (only required if
statefulis True):llrs_ch ([…,n], tf.float32) – 2+D tensor containing the channel logits/llr values.
msg_vn (None or RaggedTensor, tf.float32) – Ragged tensor of VN messages. Required only if
statefulis True.
- Output:
[…,n], tf.float32 – 2+D Tensor of same shape as
inputscontaining bit-wise soft-estimates (or hard-decided bit-values) of all codeword bits.RaggedTensor, tf.float32: – Tensor of VN messages. Returned only if
statefulis set to True.
- Attributes:
pcm (ndarray) – An ndarray of shape [n-k, n] defining the parity-check matrix consisting only of 0 or 1 entries. Can be also of type scipy. sparse.csr_matrix or scipy.sparse.csc_matrix.
num_cns (int) – Defining the number of check nodes.
num_vns (int) – Defining the number of variable nodes.
num_edges (int) – Defining the total number of edges.
trainable (bool) – If True, the decoder uses trainable weights.
_atanh_clip_value (float) – Defining the internal clipping value before the atanh is applied (relates to the CN update).
_cn_type (str) – Defining the CN update function type.
_cn_update – A function defining the CN update.
_hard_out (bool) – If True, the decoder outputs hard-decided bits.
_cn_con (ndarray) – An ndarray of shape [num_edges] defining all edges from check node perspective.
_vn_con (ndarray) – An ndarray of shape [num_edges] defining all edges from variable node perspective.
_vn_mask_tf (tf.float32) – A ragged Tensor of shape [num_vns, None] defining the incoming message indices per VN. The second dimension is ragged and depends on the node degree.
_cn_mask_tf (tf.float32) – A ragged Tensor of shape [num_cns, None] defining the incoming message indices per CN. The second dimension is ragged and depends on the node degree.
_ind_cn (ndarray) – An ndarray of shape [num_edges] defining the permutation index to rearrange messages from variable into check node perspective.
_ind_cn_inv (ndarray) – An ndarray of shape [num_edges] defining the permutation index to rearrange messages from check into variable node perspective.
_vn_row_splits (ndarray) – An ndarray of shape [num_vns+1] defining the row split positions of a 1D vector consisting of all edges messages. Used to build a ragged Tensor of incoming VN messages.
_cn_row_splits (ndarray) – An ndarray of shape [num_cns+1] defining the row split positions of a 1D vector consisting of all edges messages. Used to build a ragged Tensor of incoming CN messages.
_edge_weights (tf.float32) – A Tensor of shape [num_edges] defining a (trainable) weight per outgoing VN message.
- Raises:
ValueError – If the shape of
pcmis invalid or contains other values than 0 or 1 or dtype is not tf.float32.ValueError – If
num_iteris not an integer greater (or equal) 0.ValueError – If
output_dtypeis not {tf.float16, tf.float32, tf.float64}.ValueError – If
inputsis not of shape [batch_size, n].InvalidArgumentError – When rank(
inputs)<2.
Note
As decoding input logits \(\operatorname{log} \frac{p(x=1)}{p(x=0)}\) are assumed for compatibility with the learning framework, but internally log-likelihood ratios (LLRs) with definition \(\operatorname{log} \frac{p(x=0)}{p(x=1)}\) are used.
The decoder is not (particularly) optimized for quasi-cyclic (QC) LDPC codes and, thus, supports arbitrary parity-check matrices.
The decoder is implemented by using ‘“ragged Tensors”’ [TF_ragged] to account for arbitrary node degrees. To avoid a performance degradation caused by a severe indexing overhead, the batch-dimension is shifted to the last dimension during decoding.
If the decoder is made trainable [Nachmani], for performance improvements only variable to check node messages are scaled as the VN operation is linear and, thus, would not increase the expressive power of the weights.
- property edge_weights
Trainable weights of the BP decoder.
- property has_weights
Indicates if decoder has trainable weights.
- property ie_c
Extrinsic mutual information at check node.
- property ie_v
Extrinsic mutual information at variable node.
- property llr_max
Max LLR value used for internal calculations and rate-matching.
- property num_cns
Number of check nodes.
- property num_edges
Number of edges in decoding graph.
- property num_iter
Number of decoding iterations.
- property num_vns
Number of variable nodes.
- property output_dtype
Output dtype of decoder.
- property pcm
Parity-check matrix of LDPC code.
LDPC5GDecoder
- class sionna.fec.ldpc.decoding.LDPC5GDecoder(encoder, trainable=False, cn_type='boxplus-phi', hard_out=True, track_exit=False, return_infobits=True, prune_pcm=True, num_iter=20, stateful=False, output_dtype=tf.float32, **kwargs)[source]
(Iterative) belief propagation decoder for 5G NR LDPC codes.
Inherits from
LDPCBPDecoderand provides a wrapper for 5G compatibility, i.e., automatically handles puncturing and shortening according to [3GPPTS38212_LDPC].Note that for full 5G 3GPP NR compatibility, the correct puncturing and shortening patterns must be applied and, thus, the encoder object is required as input.
If required the decoder can be made trainable and is differentiable (the training of some check node types may be not supported) following the concept of “weighted BP” [Nachmani].
For numerical stability, the decoder applies LLR clipping of +/- 20 to the input LLRs.
The class inherits from the Keras layer class and can be used as layer in a Keras model.
- Parameters:
encoder (LDPC5GEncoder) – An instance of
LDPC5GEncodercontaining the correct code parameters.trainable (bool) – Defaults to False. If True, every outgoing variable node message is scaled with a trainable scalar.
cn_type (str) – A string defaults to ‘“boxplus-phi”’. One of {“boxplus”, “boxplus-phi”, “minsum”} where ‘“boxplus”’ implements the single-parity-check APP decoding rule. ‘“boxplus-phi”’ implements the numerical more stable version of boxplus [Ryan]. ‘“minsum”’ implements the min-approximation of the CN update rule [Ryan].
hard_out (bool) – Defaults to True. If True, the decoder provides hard-decided codeword bits instead of soft-values.
track_exit (bool) – Defaults to False. If True, the decoder tracks EXIT characteristics. Note that this requires the all-zero CW as input.
return_infobits (bool) – Defaults to True. If True, only the k info bits (soft or hard-decided) are returned. Otherwise all n positions are returned.
prune_pcm (bool) – Defaults to True. If True, all punctured degree-1 VNs and connected check nodes are removed from the decoding graph (see [Cammerer] for details). Besides numerical differences, this should yield the same decoding result but improved the decoding throughput and reduces the memory footprint.
num_iter (int) – Defining the number of decoder iteration (no early stopping used at the moment!).
stateful (bool) – Defaults to False. If True, the internal VN messages
msg_vnfrom the last decoding iteration are returned, andmsg_vnor None needs to be given as a second input when calling the decoder. This is required for iterative demapping and decoding.output_dtype (tf.DType) – Defaults to tf.float32. Defines the output datatype of the layer (internal precision remains tf.float32).
- Input:
llrs_ch or (llrs_ch, msg_vn) – Tensor or Tuple (only required if
statefulis True):llrs_ch ([…,n], tf.float32) – 2+D tensor containing the channel logits/llr values.
msg_vn (None or RaggedTensor, tf.float32) – Ragged tensor of VN messages. Required only if
statefulis True.
- Output:
[…,n] or […,k], tf.float32 – 2+D Tensor of same shape as
inputscontaining bit-wise soft-estimates (or hard-decided bit-values) of all codeword bits. Ifreturn_infobitsis True, only the k information bits are returned.RaggedTensor, tf.float32: – Tensor of VN messages. Returned only if
statefulis set to True.
- Raises:
ValueError – If the shape of
pcmis invalid or contains other values than 0 or 1.AssertionError – If
trainableis not bool.AssertionError – If
track_exitis not bool.AssertionError – If
hard_outis not bool.AssertionError – If
return_infobitsis not bool.AssertionError – If
encoderis not an instance ofLDPC5GEncoder.ValueError – If
output_dtypeis not {tf.float16, tf.float32, tf. float64}.ValueError – If
inputsis not of shape [batch_size, n].ValueError – If
num_iteris not an integer greater (or equal) 0.InvalidArgumentError – When rank(
inputs)<2.
Note
As decoding input logits \(\operatorname{log} \frac{p(x=1)}{p(x=0)}\) are assumed for compatibility with the learning framework, but internally llrs with definition \(\operatorname{log} \frac{p(x=0)}{p(x=1)}\) are used.
The decoder is not (particularly) optimized for Quasi-cyclic (QC) LDPC codes and, thus, supports arbitrary parity-check matrices.
The decoder is implemented by using ‘“ragged Tensors”’ [TF_ragged] to account for arbitrary node degrees. To avoid a performance degradation caused by a severe indexing overhead, the batch-dimension is shifted to the last dimension during decoding.
If the decoder is made trainable [Nachmani], for performance improvements only variable to check node messages are scaled as the VN operation is linear and, thus, would not increase the expressive power of the weights.
- property encoder
LDPC Encoder used for rate-matching/recovery.
- References:
- [Pfister]
J. Hou, P. H. Siegel, L. B. Milstein, and H. D. Pfister, “Capacity-approaching bandwidth-efficient coded modulation schemes based on low-density parity-check codes,” IEEE Trans. Inf. Theory, Sep. 2003.
[3GPPTS38212_LDPC] (1,2,3,4,5,6,7)ETSI 3GPP TS 38.212 “5G NR Multiplexing and channel coding”, v.16.5.0, 2021-03.
[Ryan] (1,2,3,4,5,6)W. Ryan, “An Introduction to LDPC codes”, CRC Handbook for Coding and Signal Processing for Recording Systems, 2004.
[Richardson]T. Richardson and S. Kudekar. “Design of low-density parity-check codes for 5G new radio,” IEEE Communications Magazine 56.3, 2018.
[Nachmani] (1,2,3,4,5)E. Nachmani, Y. Be’ery, and D. Burshtein. “Learning to decode linear codes using deep learning,” IEEE Annual Allerton Conference on Communication, Control, and Computing (Allerton), 2016.
[Cammerer]S. Cammerer, M. Ebada, A. Elkelesh, and S. ten Brink. “Sparse graphs for belief propagation decoding of polar codes.” IEEE International Symposium on Information Theory (ISIT), 2018.