Orthogonal Frequency-Division Multiplexing (OFDM)

This module provides layers and functions to support simulation of OFDM-based systems. The key component is the ResourceGrid that defines how data and pilot symbols are mapped onto a sequence of OFDM symbols with a given FFT size. The resource grid can also define guard and DC carriers which are nulled. In 4G/5G parlance, a ResourceGrid would be a slot. Once a ResourceGrid is defined, one can use the ResourceGridMapper to map a tensor of complex-valued data symbols onto the resource grid, prior to OFDM modulation using the OFDMModulator or further processing in the frequency domain.

The PilotPattern allows for a fine-grained configuration of how transmitters send pilots for each of their streams or antennas. As the management of pilots in multi-cell MIMO setups can quickly become complicated, the module provides the KroneckerPilotPattern class that automatically generates orthogonal pilot transmissions for all transmitters and streams.

Additionally, the module contains layers for channel estimation, precoding, equalization, and detection, such as the LSChannelEstimator, the ZFPrecoder, and the LMMSEEqualizer and LinearDetector. These are good starting points for the development of more advanced algorithms and provide robust baselines for benchmarking.

Resource Grid

The following code snippet shows how to setup and visualize an instance of ResourceGrid:

rg = ResourceGrid(num_ofdm_symbols = 14,
                  fft_size = 64,
                  subcarrier_spacing = 30e3,
                  num_tx = 1,
                  num_streams_per_tx = 1,
                  num_guard_carriers = [5, 6],
                  dc_null = True,
                  pilot_pattern = "kronecker",
                  pilot_ofdm_symbol_indices = [2, 11])
rg.show();

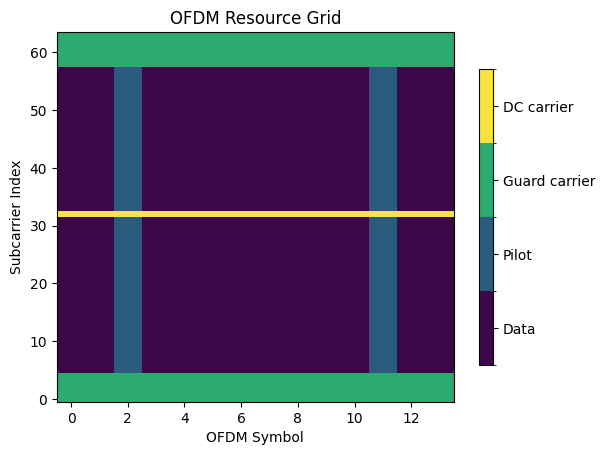
This code creates a resource grid consisting of 14 OFDM symbols with 64 subcarriers. The first five and last six subcarriers as well as the DC subcarriers are nulled. The second and eleventh OFDM symbol are reserved for pilot transmissions.

Subcarriers are numbered from \(0\) to \(N-1\), where \(N\) is the FTT size. The index \(0\) corresponds to the lowest frequency, which is \(-\frac{N}{2}\Delta_f\) (for \(N\) even) or \(-\frac{N-1}{2}\Delta_f\) (for \(N\) odd), where \(\Delta_f\) is the subcarrier spacing which is irrelevant for the resource grid. The index \(N-1\) corresponds to the highest frequency, which is \((\frac{N}{2}-1)\Delta_f\) (for \(N\) even) or \(\frac{N-1}{2}\Delta_f\) (for \(N\) odd).

ResourceGrid

class sionna.ofdm.ResourceGrid(num_ofdm_symbols, fft_size, subcarrier_spacing, num_tx=1, num_streams_per_tx=1, cyclic_prefix_length=0, num_guard_carriers=(0, 0), dc_null=False, pilot_pattern=None, pilot_ofdm_symbol_indices=None, dtype=tf.complex64)

Defines a ResourceGrid spanning multiple OFDM symbols and subcarriers.

Parameters:

• num_ofdm_symbols (int) – Number of OFDM symbols.

• fft_size (int) – FFT size (, i.e., the number of subcarriers).

• subcarrier_spacing (float) – The subcarrier spacing in Hz.

• num_tx (int) – Number of transmitters.

• num_streams_per_tx (int) – Number of streams per transmitter.

• cyclic_prefix_length (int) – Length of the cyclic prefix.

• num_guard_carriers (int) – List of two integers defining the number of guardcarriers at the left and right side of the resource grid.

• dc_null (bool) – Indicates if the DC carrier is nulled or not.

• pilot_pattern (One of [None, "kronecker", "empty", PilotPattern]) – An instance of PilotPattern, a string shorthand for the KroneckerPilotPattern or EmptyPilotPattern, or None. Defaults to None which is equivalent to “empty”.

• pilot_ofdm_symbol_indices (List, int) – List of indices of OFDM symbols reserved for pilot transmissions. Only needed if pilot_pattern="kronecker". Defaults to None.

• dtype (tf.Dtype) – Defines the datatype for internal calculations and the output dtype. Defaults to tf.complex64.

property bandwidth

fft_size*subcarrier_spacing.

Type:

The occupied bandwidth [Hz]

build_type_grid()

Returns a tensor indicating the type of each resource element.

Resource elements can be one of

• 0 : Data symbol

• 1 : Pilot symbol

• 2 : Guard carrier symbol

• 3 : DC carrier symbol

Output:

[num_tx, num_streams_per_tx, num_ofdm_symbols, fft_size], tf.int32 – Tensor indicating for each transmitter and stream the type of the resource elements of the corresponding resource grid. The type can be one of [0,1,2,3] as explained above.

property cyclic_prefix_length

Length of the cyclic prefix.

property dc_ind

Index of the DC subcarrier.

If fft_size is odd, the index is (fft_size-1)/2. If fft_size is even, the index is fft_size/2.

property dc_null

Indicates if the DC carriers is nulled or not.

property effective_subcarrier_ind

Returns the indices of the effective subcarriers.

property fft_size

The FFT size.

property num_data_symbols

Number of resource elements used for data transmissions.

property num_effective_subcarriers

Number of subcarriers used for data and pilot transmissions.

property num_guard_carriers

Number of left and right guard carriers.

property num_ofdm_symbols

The number of OFDM symbols of the resource grid.

property num_pilot_symbols

Number of resource elements used for pilot symbols.

property num_resource_elements

Number of resource elements.

property num_streams_per_tx

Number of streams per transmitter.

property num_time_samples

The number of time-domain samples occupied by the resource grid.

property num_tx

Number of transmitters.

property num_zero_symbols

Number of empty resource elements.

property ofdm_symbol_duration

Duration of an OFDM symbol with cyclic prefix [s].

property pilot_pattern

The used PilotPattern.

show(tx_ind=0, tx_stream_ind=0)

Visualizes the resource grid for a specific transmitter and stream.

Input:

• tx_ind (int) – Indicates the transmitter index.

• tx_stream_ind (int) – Indicates the index of the stream.

Output:

matplotlib.figure – A handle to a matplot figure object.

property subcarrier_spacing

The subcarrier spacing [Hz].

ResourceGridMapper

class sionna.ofdm.ResourceGridMapper(resource_grid, dtype=tf.complex64, **kwargs)

Maps a tensor of modulated data symbols to a ResourceGrid.

This layer takes as input a tensor of modulated data symbols and maps them together with pilot symbols onto an OFDM ResourceGrid. The output can be converted to a time-domain signal with the Modulator or further processed in the frequency domain.

Parameters:

• resource_grid (ResourceGrid) – An instance of ResourceGrid.

• dtype (tf.Dtype) – Datatype for internal calculations and the output dtype. Defaults to tf.complex64.

Input:

[batch_size, num_tx, num_streams_per_tx, num_data_symbols], tf.complex – The modulated data symbols to be mapped onto the resource grid.

Output:

[batch_size, num_tx, num_streams_per_tx, num_ofdm_symbols, fft_size], tf.complex – The full OFDM resource grid in the frequency domain.

ResourceGridDemapper

class sionna.ofdm.ResourceGridDemapper(resource_grid, stream_management, dtype=tf.complex64, **kwargs)

Extracts data-carrying resource elements from a resource grid.

This layer takes as input an OFDM ResourceGrid and extracts the data-carrying resource elements. In other words, it implements the reverse operation of ResourceGridMapper.

Parameters:

• resource_grid (ResourceGrid) – An instance of ResourceGrid.

• stream_management (StreamManagement) – An instance of StreamManagement.

• dtype (tf.Dtype) – Datatype for internal calculations and the output dtype. Defaults to tf.complex64.

Input:

[batch_size, num_rx, num_streams_per_rx, num_ofdm_symbols, fft_size, data_dim] – The full OFDM resource grid in the frequency domain. The last dimension data_dim is optional. If data_dim is used, it refers to the dimensionality of the data that should be demapped to individual streams. An example would be LLRs.

Output:

[batch_size, num_rx, num_streams_per_rx, num_data_symbols, data_dim] – The data that were mapped into the resource grid. The last dimension data_dim is only returned if it was used for the input.

RemoveNulledSubcarriers

class sionna.ofdm.RemoveNulledSubcarriers(resource_grid, **kwargs)

Removes nulled guard and/or DC subcarriers from a resource grid.

Parameters:

resource_grid (ResourceGrid) – An instance of ResourceGrid.

Input:

[batch_size, num_tx, num_streams_per_tx, num_ofdm_symbols, fft_size], tf.complex64 – Full resource grid.

Output:

[batch_size, num_tx, num_streams_per_tx, num_ofdm_symbols, num_effective_subcarriers], tf.complex64 – Resource grid without nulled subcarriers.

Modulation & Demodulation

OFDMModulator

class sionna.ofdm.OFDMModulator(cyclic_prefix_length=0, **kwargs)

Computes the time-domain representation of an OFDM resource grid with (optional) cyclic prefix

Parameters:

cyclic_prefix_length (scalar or [num_ofdm_symbols], int) – Integer or vector of integers indicating the length of the cyclic prefix that is prepended to each OFDM symbol. None of its elements can be larger than the FFT size. Defaults to 0.

Input:

[…,num_ofdm_symbols,fft_size], tf.complex – Resource grid in the frequency domain

Output:

[…,num_ofdm_symbols*(fft_size+cyclic_prefix_length)] or […,num_ofdm_symbols*fft_size+sum(cyclic_prefix_length)], tf.complex – Time-domain OFDM signal

property cyclic_prefix_length

Get/set the cyclic prefix length

Type:

scalar or [num_ofdm_symbols], int

OFDMDemodulator

class sionna.ofdm.OFDMDemodulator(fft_size, l_min, cyclic_prefix_length, **kwargs)

Computes the frequency-domain representation of an OFDM waveform with cyclic prefix removal.

The demodulator assumes that the input sequence is generated by the TimeChannel. For a single pair of antennas, the received signal sequence is given as:

\[y_b = \sum_{\ell =L_\text{min}}^{L_\text{max}} \bar{h}_\ell x_{b-\ell} + w_b, \quad b \in[L_\text{min}, N_B+L_\text{max}-1]\]

where \(\bar{h}_\ell\) are the discrete-time channel taps, \(x_{b}\) is the the transmitted signal, and \(w_\ell\) Gaussian noise.

Starting from the first symbol, the demodulator cuts the input sequence into pieces of size cyclic_prefix_length + fft_size, and throws away any trailing symbols. For each piece, the cyclic prefix is removed and the fft_size-point discrete Fourier transform is computed. It is also possible that every OFDM symbol has a cyclic prefix of different length.

Since the input sequence starts at time \(L_\text{min}\), the FFT-window has a timing offset of \(L_\text{min}\) symbols, which leads to a subcarrier-dependent phase shift of \(e^{\frac{j2\pi k L_\text{min}}{N}}\), where \(k\) is the subcarrier index, \(N\) is the FFT size, and \(L_\text{min} \le 0\) is the largest negative time lag of the discrete-time channel impulse response. This phase shift is removed in this layer, by explicitly multiplying each subcarrier by \(e^{\frac{-j2\pi k L_\text{min}}{N}}\). This is a very important step to enable channel estimation with sparse pilot patterns that needs to interpolate the channel frequency response accross subcarriers. It also ensures that the channel frequency response seen by the time-domain channel is close to the OFDMChannel.

Parameters:

• fft_size (int) – FFT size (, i.e., the number of subcarriers).

• l_min (int) – The largest negative time lag of the discrete-time channel impulse response. It should be the same value as that used by the cir_to_time_channel function.

• cyclic_prefix_length (scalar or [num_ofdm_symbols], int) – Integer or vector of integers indicating the length of the cyclic prefix that is prepended to each OFDM symbol. None of its elements can be larger than the FFT size. Defaults to 0.

Input:

[…,num_ofdm_symbols*(fft_size+cyclic_prefix_length)+n] or […,num_ofdm_symbols*fft_size+sum(cyclic_prefix_length)+n], tf.complex – Tensor containing the time-domain signal along the last dimension. n is a nonnegative integer.

Output:

[…,num_ofdm_symbols,fft_size], tf.complex – Tensor containing the OFDM resource grid along the last two dimension.

Pilot Pattern

A PilotPattern defines how transmitters send pilot sequences for each of their antennas or streams over an OFDM resource grid. It consists of two components, a mask and pilots. The mask indicates which resource elements are reserved for pilot transmissions by each transmitter and its respective streams. In some cases, the number of streams is equal to the number of transmit antennas, but this does not need to be the case, e.g., for precoded transmissions. The pilots contains the pilot symbols that are transmitted at the positions indicated by the mask. Separating a pilot pattern into mask and pilots enables the implementation of a wide range of pilot configurations, including trainable pilot sequences.

The following code snippet shows how to define a simple custom PilotPattern for single transmitter, sending two streams Note that num_effective_subcarriers is the number of subcarriers that can be used for data or pilot transmissions. Due to guard carriers or a nulled DC carrier, this number can be smaller than the fft_size of the ResourceGrid.

num_tx = 1
num_streams_per_tx = 2
num_ofdm_symbols = 14
num_effective_subcarriers = 12

# Create a pilot mask
mask = np.zeros([num_tx,
                 num_streams_per_tx,
                 num_ofdm_symbols,
                 num_effective_subcarriers])
mask[0, :, [2,11], :] = 1
num_pilot_symbols = int(np.sum(mask[0,0]))

# Define pilot sequences
pilots = np.zeros([num_tx,
                   num_streams_per_tx,
                   num_pilot_symbols], np.complex64)
pilots[0, 0, 0:num_pilot_symbols:2] = (1+1j)/np.sqrt(2)
pilots[0, 1, 1:num_pilot_symbols:2] = (1+1j)/np.sqrt(2)

# Create a PilotPattern instance
pp = PilotPattern(mask, pilots)

# Visualize non-zero elements of the pilot sequence
pp.show(show_pilot_ind=True);

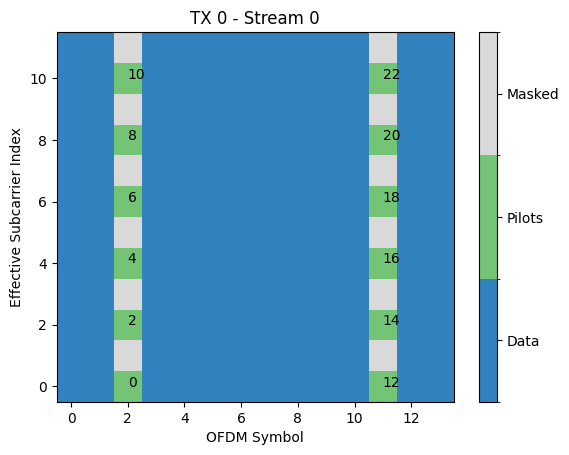
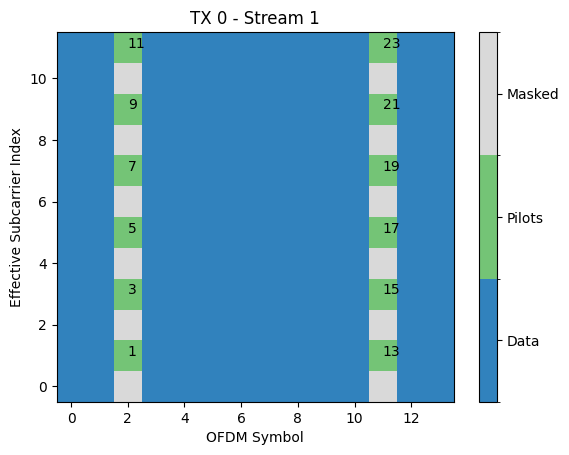
As shown in the figures above, the pilots are mapped onto the mask from the smallest effective subcarrier and OFDM symbol index to the highest effective subcarrier and OFDM symbol index. Here, boths stream have 24 pilot symbols, out of which only 12 are nonzero. It is important to keep this order of mapping in mind when designing more complex pilot sequences.

PilotPattern

class sionna.ofdm.PilotPattern(mask, pilots, trainable=False, normalize=False, dtype=tf.complex64)

Class defining a pilot pattern for an OFDM ResourceGrid.

This class defines a pilot pattern object that is used to configure an OFDM ResourceGrid.

Parameters:

• mask ([num_tx, num_streams_per_tx, num_ofdm_symbols, num_effective_subcarriers], bool) – Tensor indicating resource elements that are reserved for pilot transmissions.

• pilots ([num_tx, num_streams_per_tx, num_pilots], tf.complex) – The pilot symbols to be mapped onto the mask.

• trainable (bool) – Indicates if pilots is a trainable Variable. Defaults to False.

• normalize (bool) – Indicates if the pilots should be normalized to an average energy of one across the last dimension. This can be useful to ensure that trainable pilots have a finite energy. Defaults to False.

• dtype (tf.Dtype) – Defines the datatype for internal calculations and the output dtype. Defaults to tf.complex64.

property mask

Mask of the pilot pattern

property normalize

Returns or sets the flag indicating if the pilots are normalized or not

property num_data_symbols

Number of data symbols per transmit stream.

property num_effective_subcarriers

Number of effectvie subcarriers

property num_ofdm_symbols

Number of OFDM symbols

property num_pilot_symbols

Number of pilot symbols per transmit stream.

property num_streams_per_tx

Number of streams per transmitter

property num_tx

Number of transmitters

property pilots

Returns or sets the possibly normalized tensor of pilot symbols. If pilots are normalized, the normalization will be applied after new values for pilots have been set. If this is not the desired behavior, turn normalization off.

show(tx_ind=None, stream_ind=None, show_pilot_ind=False)

Visualizes the pilot patterns for some transmitters and streams.

Input:

• tx_ind (list, int) – Indicates the indices of transmitters to be included. Defaults to None, i.e., all transmitters included.

• stream_ind (list, int) – Indicates the indices of streams to be included. Defaults to None, i.e., all streams included.

• show_pilot_ind (bool) – Indicates if the indices of the pilot symbols should be shown.

Output:

list (matplotlib.figure.Figure) – List of matplot figure objects showing each the pilot pattern from a specific transmitter and stream.

property trainable

Returns if pilots are trainable or not

EmptyPilotPattern

class sionna.ofdm.EmptyPilotPattern(num_tx, num_streams_per_tx, num_ofdm_symbols, num_effective_subcarriers, dtype=tf.complex64)

Creates an empty pilot pattern.

Generates a instance of PilotPattern with an empty mask and pilots.

Parameters:

• num_tx (int) – Number of transmitters.

• num_streams_per_tx (int) – Number of streams per transmitter.

• num_ofdm_symbols (int) – Number of OFDM symbols.

• num_effective_subcarriers (int) – Number of effective subcarriers that are available for the transmission of data and pilots. Note that this number is generally smaller than the fft_size due to nulled subcarriers.

• dtype (tf.Dtype) – Defines the datatype for internal calculations and the output dtype. Defaults to tf.complex64.

KroneckerPilotPattern

class sionna.ofdm.KroneckerPilotPattern(resource_grid, pilot_ofdm_symbol_indices, normalize=True, seed=0, dtype=tf.complex64)

Simple orthogonal pilot pattern with Kronecker structure.

This function generates an instance of PilotPattern that allocates non-overlapping pilot sequences for all transmitters and streams on specified OFDM symbols. As the same pilot sequences are reused across those OFDM symbols, the resulting pilot pattern has a frequency-time Kronecker structure. This structure enables a very efficient implementation of the LMMSE channel estimator. Each pilot sequence is constructed from randomly drawn QPSK constellation points.

Parameters:

• resource_grid (ResourceGrid) – An instance of a ResourceGrid.

• pilot_ofdm_symbol_indices (list, int) – List of integers defining the OFDM symbol indices that are reserved for pilots.

• normalize (bool) – Indicates if the pilots should be normalized to an average energy of one across the last dimension. Defaults to True.

• seed (int) – Seed for the generation of the pilot sequence. Different seed values lead to different sequences. Defaults to 0.

• dtype (tf.Dtype) – Defines the datatype for internal calculations and the output dtype. Defaults to tf.complex64.

Note

It is required that the resource_grid’s property num_effective_subcarriers is an integer multiple of num_tx * num_streams_per_tx. This condition is required to ensure that all transmitters and streams get non-overlapping pilot sequences. For a large number of streams and/or transmitters, the pilot pattern becomes very sparse in the frequency domain.

Examples

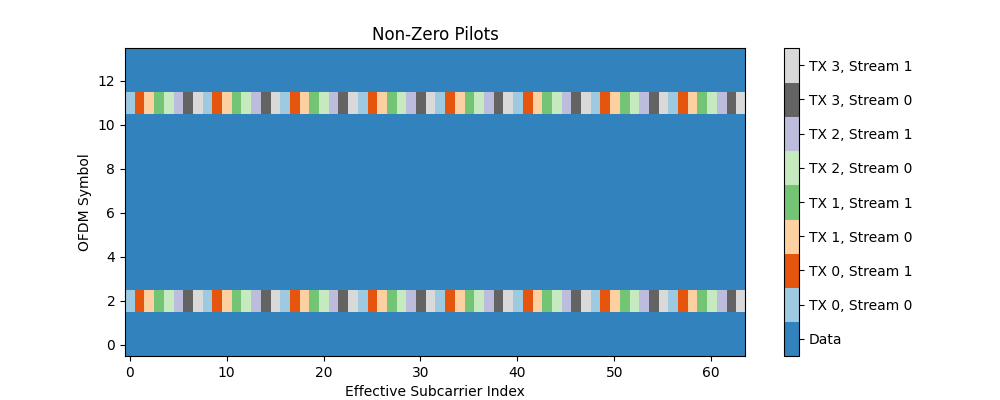
>>> rg = ResourceGrid(num_ofdm_symbols=14,
...                   fft_size=64,
...                   subcarrier_spacing = 30e3,
...                   num_tx=4,
...                   num_streams_per_tx=2,
...                   pilot_pattern = "kronecker",
...                   pilot_ofdm_symbol_indices = [2, 11])
>>> rg.pilot_pattern.show();

Channel Estimation

BaseChannelEstimator

class sionna.ofdm.BaseChannelEstimator(resource_grid, interpolation_type='nn', interpolator=None, dtype=tf.complex64, **kwargs)

Abstract layer for implementing an OFDM channel estimator.

Any layer that implements an OFDM channel estimator must implement this class and its estimate_at_pilot_locations() abstract method.

This class extracts the pilots from the received resource grid y, calls the estimate_at_pilot_locations() method to estimate the channel for the pilot-carrying resource elements, and then interpolates the channel to compute channel estimates for the data-carrying resouce elements using the interpolation method specified by interpolation_type or the interpolator object.

Parameters:

• resource_grid (ResourceGrid) – An instance of ResourceGrid.

• interpolation_type (One of ["nn", "lin", "lin_time_avg"], string) – The interpolation method to be used. It is ignored if interpolator is not None. Available options are NearestNeighborInterpolator (“nn”) or LinearInterpolator without (“lin”) or with averaging across OFDM symbols (“lin_time_avg”). Defaults to “nn”.

• interpolator (BaseChannelInterpolator) – An instance of BaseChannelInterpolator, such as LMMSEInterpolator, or None. In the latter case, the interpolator specfied by interpolation_type is used. Otherwise, the interpolator is used and interpolation_type is ignored. Defaults to None.

• dtype (tf.Dtype) – Datatype for internal calculations and the output dtype. Defaults to tf.complex64.

Input:

• (y, no) – Tuple:

• y ([batch_size, num_rx, num_rx_ant, num_ofdm_symbols,fft_size], tf.complex) – Observed resource grid

• no ([batch_size, num_rx, num_rx_ant] or only the first n>=0 dims, tf.float) – Variance of the AWGN

Output:

• h_hat ([batch_size, num_rx, num_rx_ant, num_tx, num_streams_per_tx, num_ofdm_symbols,fft_size], tf.complex) – Channel estimates accross the entire resource grid for all transmitters and streams

• err_var (Same shape as h_hat, tf.float) – Channel estimation error variance accross the entire resource grid for all transmitters and streams

abstract estimate_at_pilot_locations(y_pilots, no)

Estimates the channel for the pilot-carrying resource elements.

This is an abstract method that must be implemented by a concrete OFDM channel estimator that implement this class.

Input:

• y_pilots ([batch_size, num_rx, num_rx_ant, num_tx, num_streams, num_pilot_symbols], tf.complex) – Observed signals for the pilot-carrying resource elements

• no ([batch_size, num_rx, num_rx_ant] or only the first n>=0 dims, tf.float) – Variance of the AWGN

Output:

• h_hat ([batch_size, num_rx, num_rx_ant, num_tx, num_streams, num_pilot_symbols], tf.complex) – Channel estimates for the pilot-carrying resource elements

• err_var (Same shape as h_hat, tf.float) – Channel estimation error variance for the pilot-carrying resource elements

BaseChannelInterpolator

class sionna.ofdm.BaseChannelInterpolator

Abstract layer for implementing an OFDM channel interpolator.

Any layer that implements an OFDM channel interpolator must implement this callable class.

A channel interpolator is used by an OFDM channel estimator (BaseChannelEstimator) to compute channel estimates for the data-carrying resource elements from the channel estimates for the pilot-carrying resource elements.

Input:

• h_hat ([batch_size, num_rx, num_rx_ant, num_tx, num_streams_per_tx, num_pilot_symbols], tf.complex) – Channel estimates for the pilot-carrying resource elements

• err_var ([batch_size, num_rx, num_rx_ant, num_tx, num_streams_per_tx, num_pilot_symbols], tf.complex) – Channel estimation error variances for the pilot-carrying resource elements

Output:

• h_hat ([batch_size, num_rx, num_rx_ant, num_tx, num_streams_per_tx, num_ofdm_symbols, fft_size], tf.complex) – Channel estimates accross the entire resource grid for all transmitters and streams

• err_var (Same shape as h_hat, tf.float) – Channel estimation error variance accross the entire resource grid for all transmitters and streams

LSChannelEstimator

class sionna.ofdm.LSChannelEstimator(resource_grid, interpolation_type='nn', interpolator=None, dtype=tf.complex64, **kwargs)

Layer implementing least-squares (LS) channel estimation for OFDM MIMO systems.

After LS channel estimation at the pilot positions, the channel estimates and error variances are interpolated accross the entire resource grid using a specified interpolation function.

For simplicity, the underlying algorithm is described for a vectorized observation, where we have a nonzero pilot for all elements to be estimated. The actual implementation works on a full OFDM resource grid with sparse pilot patterns. The following model is assumed:

\[\mathbf{y} = \mathbf{h}\odot\mathbf{p} + \mathbf{n}\]

where \(\mathbf{y}\in\mathbb{C}^{M}\) is the received signal vector, \(\mathbf{p}\in\mathbb{C}^M\) is the vector of pilot symbols, \(\mathbf{h}\in\mathbb{C}^{M}\) is the channel vector to be estimated, and \(\mathbf{n}\in\mathbb{C}^M\) is a zero-mean noise vector whose elements have variance \(N_0\). The operator \(\odot\) denotes element-wise multiplication.

The channel estimate \(\hat{\mathbf{h}}\) and error variances \(\sigma^2_i\), \(i=0,\dots,M-1\), are computed as

\[\begin{split}\hat{\mathbf{h}} &= \mathbf{y} \odot \frac{\mathbf{p}^\star}{\left|\mathbf{p}\right|^2} = \mathbf{h} + \tilde{\mathbf{h}}\\ \sigma^2_i &= \mathbb{E}\left[\tilde{h}_i \tilde{h}_i^\star \right] = \frac{N_0}{\left|p_i\right|^2}.\end{split}\]

The channel estimates and error variances are then interpolated accross the entire resource grid.

Parameters:

• resource_grid (ResourceGrid) – An instance of ResourceGrid.

• interpolation_type (One of ["nn", "lin", "lin_time_avg"], string) – The interpolation method to be used. It is ignored if interpolator is not None. Available options are NearestNeighborInterpolator (“nn”) or LinearInterpolator without (“lin”) or with averaging across OFDM symbols (“lin_time_avg”). Defaults to “nn”.

• interpolator (BaseChannelInterpolator) – An instance of BaseChannelInterpolator, such as LMMSEInterpolator, or None. In the latter case, the interpolator specfied by interpolation_type is used. Otherwise, the interpolator is used and interpolation_type is ignored. Defaults to None.

• dtype (tf.Dtype) – Datatype for internal calculations and the output dtype. Defaults to tf.complex64.

Input:

• (y, no) – Tuple:

• y ([batch_size, num_rx, num_rx_ant, num_ofdm_symbols,fft_size], tf.complex) – Observed resource grid

• no ([batch_size, num_rx, num_rx_ant] or only the first n>=0 dims, tf.float) – Variance of the AWGN

Output:

• h_ls ([batch_size, num_rx, num_rx_ant, num_tx, num_streams_per_tx, num_ofdm_symbols,fft_size], tf.complex) – Channel estimates accross the entire resource grid for all transmitters and streams

• err_var (Same shape as h_ls, tf.float) – Channel estimation error variance accross the entire resource grid for all transmitters and streams

LinearInterpolator

class sionna.ofdm.LinearInterpolator(pilot_pattern, time_avg=False)

Linear channel estimate interpolation on a resource grid.

This class computes for each element of an OFDM resource grid a channel estimate based on num_pilots provided channel estimates and error variances through linear interpolation. It is assumed that the measurements were taken at the nonzero positions of a PilotPattern.

The interpolation is done first across sub-carriers and then across OFDM symbols.

Parameters:

• pilot_pattern (PilotPattern) – An instance of PilotPattern

• time_avg (bool) – If enabled, measurements will be averaged across OFDM symbols (i.e., time). This is useful for channels that do not vary substantially over the duration of an OFDM frame. Defaults to False.

Input:

• h_hat ([batch_size, num_rx, num_rx_ant, num_tx, num_streams_per_tx, num_pilot_symbols], tf.complex) – Channel estimates for the pilot-carrying resource elements

• err_var ([batch_size, num_rx, num_rx_ant, num_tx, num_streams_per_tx, num_pilot_symbols], tf.complex) – Channel estimation error variances for the pilot-carrying resource elements

Output:

• h_hat ([batch_size, num_rx, num_rx_ant, num_tx, num_streams_per_tx, num_ofdm_symbols, fft_size], tf.complex) – Channel estimates accross the entire resource grid for all transmitters and streams

• err_var (Same shape as h_hat, tf.float) – Channel estimation error variances accross the entire resource grid for all transmitters and streams

LMMSEInterpolator

class sionna.ofdm.LMMSEInterpolator(pilot_pattern, cov_mat_time, cov_mat_freq, cov_mat_space=None, order='t-f')

LMMSE interpolation on a resource grid with optional spatial smoothing.

This class computes for each element of an OFDM resource grid a channel estimate and error variance through linear minimum mean square error (LMMSE) interpolation/smoothing. It is assumed that the measurements were taken at the nonzero positions of a PilotPattern.

Depending on the value of order, the interpolation is carried out accross time (t), i.e., OFDM symbols, frequency (f), i.e., subcarriers, and optionally space (s), i.e., receive antennas, in any desired order.

For simplicity, we describe the underlying algorithm assuming that interpolation across the sub-carriers is performed first, followed by interpolation across OFDM symbols, and finally by spatial smoothing across receive antennas. The algorithm is similar if interpolation and/or smoothing are performed in a different order. For clarity, antenna indices are omitted when describing frequency and time interpolation, as the same process is applied to all the antennas.

The input h_hat is first reshaped to a resource grid \(\hat{\mathbf{H}} \in \mathbb{C}^{N \times M}\), by scattering the channel estimates at pilot locations according to the pilot_pattern. \(N\) denotes the number of OFDM symbols and \(M\) the number of sub-carriers.

The first pass consists in interpolating across the sub-carriers:

\[\hat{\mathbf{h}}_n^{(1)} = \mathbf{A}_n \hat{\mathbf{h}}_n\]

where \(1 \leq n \leq N\) is the OFDM symbol index and \(\hat{\mathbf{h}}_n\) is the \(n^{\text{th}}\) (transposed) row of \(\hat{\mathbf{H}}\). \(\mathbf{A}_n\) is the \(M \times M\) matrix such that:

\[\mathbf{A}_n = \bar{\mathbf{A}}_n \mathbf{\Pi}_n^\intercal\]

where

\[\bar{\mathbf{A}}_n = \underset{\mathbf{Z} \in \mathbb{C}^{M \times K_n}}{\text{argmin}} \left\lVert \mathbf{Z}\left( \mathbf{\Pi}_n^\intercal \mathbf{R^{(f)}} \mathbf{\Pi}_n + \mathbf{\Sigma}_n \right) - \mathbf{R^{(f)}} \mathbf{\Pi}_n \right\rVert_{\text{F}}^2\]

and \(\mathbf{R^{(f)}}\) is the \(M \times M\) channel frequency covariance matrix, \(\mathbf{\Pi}_n\) the \(M \times K_n\) matrix that spreads \(K_n\) values to a vector of size \(M\) according to the pilot_pattern for the \(n^{\text{th}}\) OFDM symbol, and \(\mathbf{\Sigma}_n \in \mathbb{R}^{K_n \times K_n}\) is the channel estimation error covariance built from err_var and assumed to be diagonal. Computation of \(\bar{\mathbf{A}}_n\) is done using an algorithm based on complete orthogonal decomposition. This is done to avoid matrix inversion for badly conditioned covariance matrices.

The channel estimation error variances after the first interpolation pass are computed as

\[\mathbf{\Sigma}^{(1)}_n = \text{diag} \left( \mathbf{R^{(f)}} - \mathbf{A}_n \mathbf{\Xi}_n \mathbf{R^{(f)}} \right)\]

where \(\mathbf{\Xi}_n\) is the diagonal matrix of size \(M \times M\) that zeros the columns corresponding to sub-carriers not carrying any pilots. Note that interpolation is not performed for OFDM symbols which do not carry pilots.

Remark: The interpolation matrix differs across OFDM symbols as different OFDM symbols may carry pilots on different sub-carriers and/or have different estimation error variances.

Scaling of the estimates is then performed to ensure that their variances match the ones expected by the next interpolation step, and the error variances are updated accordingly:

\[\begin{split}\begin{align} \left[\hat{\mathbf{h}}_n^{(2)}\right]_m &= s_{n,m} \left[\hat{\mathbf{h}}_n^{(1)}\right]_m\\ \left[\mathbf{\Sigma}^{(2)}_n\right]_{m,m} &= s_{n,m}\left( s_{n,m}-1 \right) \left[\hat{\mathbf{\Sigma}}^{(1)}_n\right]_{m,m} + \left( 1 - s_{n,m} \right) \left[\mathbf{R^{(f)}}\right]_{m,m} + s_{n,m} \left[\mathbf{\Sigma}^{(1)}_n\right]_{m,m} \end{align}\end{split}\]

where the scaling factor \(s_{n,m}\) is such that:

\[\mathbb{E} \left\{ \left\lvert s_{n,m} \left[\hat{\mathbf{h}}_n^{(1)}\right]_m \right\rvert^2 \right\} = \left[\mathbf{R^{(f)}}\right]_{m,m} + \mathbb{E} \left\{ \left\lvert s_{n,m} \left[\hat{\mathbf{h}}^{(1)}_n\right]_m - \left[\mathbf{h}_n\right]_m \right\rvert^2 \right\}\]

which leads to:

\[\begin{split}\begin{align} s_{n,m} &= \frac{2 \left[\mathbf{R^{(f)}}\right]_{m,m}}{\left[\mathbf{R^{(f)}}\right]_{m,m} - \left[\mathbf{\Sigma}^{(1)}_n\right]_{m,m} + \left[\hat{\mathbf{\Sigma}}^{(1)}_n\right]_{m,m}}\\ \hat{\mathbf{\Sigma}}^{(1)}_n &= \mathbf{A}_n \mathbf{R^{(f)}} \mathbf{A}_n^{\mathrm{H}}. \end{align}\end{split}\]

The second pass consists in interpolating across the OFDM symbols:

\[\hat{\mathbf{h}}_m^{(3)} = \mathbf{B}_m \tilde{\mathbf{h}}^{(2)}_m\]

where \(1 \leq m \leq M\) is the sub-carrier index and \(\tilde{\mathbf{h}}^{(2)}_m\) is the \(m^{\text{th}}\) column of

\[\begin{split}\hat{\mathbf{H}}^{(2)} = \begin{bmatrix} {\hat{\mathbf{h}}_1^{(2)}}^\intercal\\ \vdots\\ {\hat{\mathbf{h}}_N^{(2)}}^\intercal \end{bmatrix}\end{split}\]

and \(\mathbf{B}_m\) is the \(N \times N\) interpolation LMMSE matrix:

\[\mathbf{B}_m = \bar{\mathbf{B}}_m \tilde{\mathbf{\Pi}}_m^\intercal\]

where

\[\bar{\mathbf{B}}_m = \underset{\mathbf{Z} \in \mathbb{C}^{N \times L_m}}{\text{argmin}} \left\lVert \mathbf{Z} \left( \tilde{\mathbf{\Pi}}_m^\intercal \mathbf{R^{(t)}}\tilde{\mathbf{\Pi}}_m + \tilde{\mathbf{\Sigma}}^{(2)}_m \right) - \mathbf{R^{(t)}}\tilde{\mathbf{\Pi}}_m \right\rVert_{\text{F}}^2\]

where \(\mathbf{R^{(t)}}\) is the \(N \times N\) channel time covariance matrix, \(\tilde{\mathbf{\Pi}}_m\) the \(N \times L_m\) matrix that spreads \(L_m\) values to a vector of size \(N\) according to the pilot_pattern for the \(m^{\text{th}}\) sub-carrier, and \(\tilde{\mathbf{\Sigma}}^{(2)}_m \in \mathbb{R}^{L_m \times L_m}\) is the diagonal matrix of channel estimation error variances built by gathering the error variances from (\(\mathbf{\Sigma}^{(2)}_1,\dots,\mathbf{\Sigma}^{(2)}_N\)) corresponding to resource elements carried by the \(m^{\text{th}}\) sub-carrier. Computation of \(\bar{\mathbf{B}}_m\) is done using an algorithm based on complete orthogonal decomposition. This is done to avoid matrix inversion for badly conditioned covariance matrices.

The resulting channel estimate for the resource grid is

\[\hat{\mathbf{H}}^{(3)} = \left[ \hat{\mathbf{h}}_1^{(3)} \dots \hat{\mathbf{h}}_M^{(3)} \right]\]

The resulting channel estimation error variances are the diagonal coefficients of the matrices

\[\mathbf{\Sigma}^{(3)}_m = \mathbf{R^{(t)}} - \mathbf{B}_m \tilde{\mathbf{\Xi}}_m \mathbf{R^{(t)}}, 1 \leq m \leq M\]

where \(\tilde{\mathbf{\Xi}}_m\) is the diagonal matrix of size \(N \times N\) that zeros the columns corresponding to OFDM symbols not carrying any pilots.

Remark: The interpolation matrix differs across sub-carriers as different sub-carriers may have different estimation error variances computed by the first pass. However, all sub-carriers carry at least one channel estimate as a result of the first pass, ensuring that a channel estimate is computed for all the resource elements after the second pass.

Remark: LMMSE interpolation requires knowledge of the time and frequency covariance matrices of the channel. The notebook OFDM MIMO Channel Estimation and Detection shows how to estimate such matrices for arbitrary channel models. Moreover, the functions tdl_time_cov_mat() and tdl_freq_cov_mat() compute the expected time and frequency covariance matrices, respectively, for the TDL channel models.

Scaling of the estimates is then performed to ensure that their variances match the ones expected by the next smoothing step, and the error variances are updated accordingly:

\[\begin{split}\begin{align} \left[\hat{\mathbf{h}}_m^{(4)}\right]_n &= \gamma_{m,n} \left[\hat{\mathbf{h}}_m^{(3)}\right]_n\\ \left[\mathbf{\Sigma}^{(4)}_m\right]_{n,n} &= \gamma_{m,n}\left( \gamma_{m,n}-1 \right) \left[\hat{\mathbf{\Sigma}}^{(3)}_m\right]_{n,n} + \left( 1 - \gamma_{m,n} \right) \left[\mathbf{R^{(t)}}\right]_{n,n} + \gamma_{m,n} \left[\mathbf{\Sigma}^{(3)}_n\right]_{m,m} \end{align}\end{split}\]

where:

\[\begin{split}\begin{align} \gamma_{m,n} &= \frac{2 \left[\mathbf{R^{(t)}}\right]_{n,n}}{\left[\mathbf{R^{(t)}}\right]_{n,n} - \left[\mathbf{\Sigma}^{(3)}_m\right]_{n,n} + \left[\hat{\mathbf{\Sigma}}^{(3)}_n\right]_{m,m}}\\ \hat{\mathbf{\Sigma}}^{(3)}_m &= \mathbf{B}_m \mathbf{R^{(t)}} \mathbf{B}_m^{\mathrm{H}} \end{align}\end{split}\]

Finally, a spatial smoothing step is applied to every resource element carrying a channel estimate. For clarity, we drop the resource element indexing \((n,m)\). We denote by \(L\) the number of receive antennas, and by \(\mathbf{R^{(s)}}\in\mathbb{C}^{L \times L}\) the spatial covariance matrix.

LMMSE spatial smoothing consists in the following computations:

\[\hat{\mathbf{h}}^{(5)} = \mathbf{C} \hat{\mathbf{h}}^{(4)}\]

where

\[\mathbf{C} = \mathbf{R^{(s)}} \left( \mathbf{R^{(s)}} + \mathbf{\Sigma}^{(4)} \right)^{-1}.\]

The estimation error variances are the digonal coefficients of

\[\mathbf{\Sigma}^{(5)} = \mathbf{R^{(s)}} - \mathbf{C}\mathbf{R^{(s)}}\]

The smoothed channel estimate \(\hat{\mathbf{h}}^{(5)}\) and corresponding error variances \(\text{diag}\left( \mathbf{\Sigma}^{(5)} \right)\) are returned for every resource element \((m,n)\).

Remark: No scaling is performed after the last interpolation or smoothing step.

Remark: All passes assume that the estimation error covariance matrix (\(\mathbf{\Sigma}\), \(\tilde{\mathbf{\Sigma}}^{(2)}\), or \(\tilde{\mathbf{\Sigma}}^{(4)}\)) is diagonal, which may not be accurate. When this assumption does not hold, this interpolator is only an approximation of LMMSE interpolation.

Remark: The order in which frequency interpolation, temporal interpolation, and, optionally, spatial smoothing are applied, is controlled using the order parameter.

Note

This layer does not support graph mode with XLA.

Parameters:

• pilot_pattern (PilotPattern) – An instance of PilotPattern

• cov_mat_time ([num_ofdm_symbols, num_ofdm_symbols], tf.complex) – Time covariance matrix of the channel

• cov_mat_freq ([fft_size, fft_size], tf.complex) – Frequency covariance matrix of the channel

• cov_time_space ([num_rx_ant, num_rx_ant], tf.complex) – Spatial covariance matrix of the channel. Defaults to None. Only required if spatial smoothing is requested (see order).

• order (str) – Order in which to perform interpolation and optional smoothing. For example, "t-f-s" means that interpolation across the OFDM symbols is performed first ("t": time), followed by interpolation across the sub-carriers ("f": frequency), and finally smoothing across the receive antennas ("s": space). Similarly, "f-t" means interpolation across the sub-carriers followed by interpolation across the OFDM symbols and no spatial smoothing. The spatial covariance matrix (cov_time_space) is only required when spatial smoothing is requested. Time and frequency interpolation are not optional to ensure that a channel estimate is computed for all resource elements.

Input:

• h_hat ([batch_size, num_rx, num_rx_ant, num_tx, num_streams_per_tx, num_pilot_symbols], tf.complex) – Channel estimates for the pilot-carrying resource elements

• err_var ([batch_size, num_rx, num_rx_ant, num_tx, num_streams_per_tx, num_pilot_symbols], tf.complex) – Channel estimation error variances for the pilot-carrying resource elements

Output:

• h_hat ([batch_size, num_rx, num_rx_ant, num_tx, num_streams_per_tx, num_ofdm_symbols, fft_size], tf.complex) – Channel estimates accross the entire resource grid for all transmitters and streams

• err_var (Same shape as h_hat, tf.float) – Channel estimation error variances accross the entire resource grid for all transmitters and streams

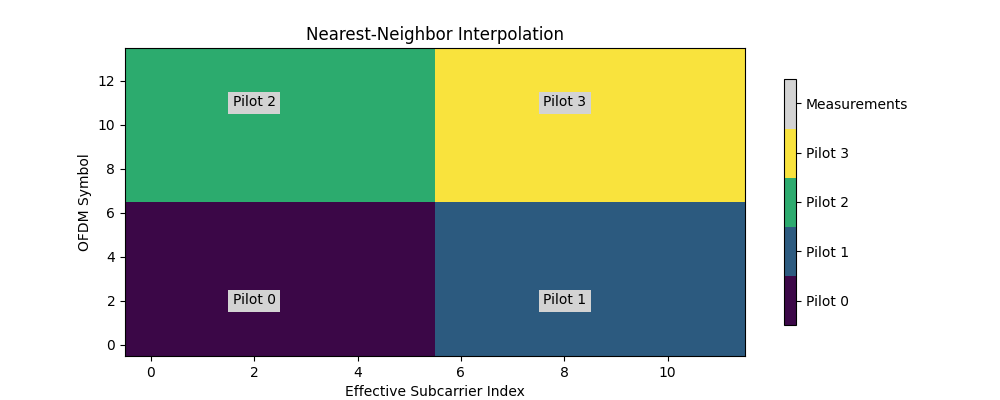
NearestNeighborInterpolator

class sionna.ofdm.NearestNeighborInterpolator(pilot_pattern)

Nearest-neighbor channel estimate interpolation on a resource grid.

This class assigns to each element of an OFDM resource grid one of num_pilots provided channel estimates and error variances according to the nearest neighbor method. It is assumed that the measurements were taken at the nonzero positions of a PilotPattern.

The figure below shows how four channel estimates are interpolated accross a resource grid. Grey fields indicate measurement positions while the colored regions show which resource elements are assigned to the same measurement value.

Parameters:

pilot_pattern (PilotPattern) – An instance of PilotPattern

Input:

• h_hat ([batch_size, num_rx, num_rx_ant, num_tx, num_streams_per_tx, num_pilot_symbols], tf.complex) – Channel estimates for the pilot-carrying resource elements

• err_var ([batch_size, num_rx, num_rx_ant, num_tx, num_streams_per_tx, num_pilot_symbols], tf.complex) – Channel estimation error variances for the pilot-carrying resource elements

Output:

• h_hat ([batch_size, num_rx, num_rx_ant, num_tx, num_streams_per_tx, num_ofdm_symbols, fft_size], tf.complex) – Channel estimates accross the entire resource grid for all transmitters and streams

• err_var (Same shape as h_hat, tf.float) – Channel estimation error variances accross the entire resource grid for all transmitters and streams

tdl_time_cov_mat

sionna.ofdm.tdl_time_cov_mat(model, speed, carrier_frequency, ofdm_symbol_duration, num_ofdm_symbols, los_angle_of_arrival=0.7853981633974483, dtype=tf.complex64)

Computes the time covariance matrix of a TDL channel model.

For non-line-of-sight (NLoS) model, the channel time covariance matrix \(\mathbf{R^{(t)}}\) of a TDL channel model is

\[\mathbf{R^{(t)}}_{u,v} = J_0 \left( \nu \Delta_t \left( u-v \right) \right)\]

where \(J_0\) is the zero-order Bessel function of the first kind, \(\Delta_t\) the duration of an OFDM symbol, and \(\nu\) the Doppler spread defined by

\[\nu = 2 \pi \frac{v}{c} f_c\]

where \(v\) is the movement speed, \(c\) the speed of light, and \(f_c\) the carrier frequency.

For line-of-sight (LoS) channel models, the channel time covariance matrix is

\[\mathbf{R^{(t)}}_{u,v} = P_{\text{NLoS}} J_0 \left( \nu \Delta_t \left( u-v \right) \right) + P_{\text{LoS}}e^{j \nu \Delta_t \left( u-v \right) \cos{\alpha_{\text{LoS}}}}\]

where \(\alpha_{\text{LoS}}\) is the angle-of-arrival for the LoS path, \(P_{\text{NLoS}}\) the total power of NLoS paths, and \(P_{\text{LoS}}\) the power of the LoS path. The power delay profile is assumed to have unit power, i.e., \(P_{\text{NLoS}} + P_{\text{LoS}} = 1\).

Input:

• model (str) – TDL model for which to return the covariance matrix. Should be one of “A”, “B”, “C”, “D”, or “E”.

• speed (float) – Speed [m/s]

• carrier_frequency (float) – Carrier frequency [Hz]

• ofdm_symbol_duration (float) – Duration of an OFDM symbol [s]

• num_ofdm_symbols (int) – Number of OFDM symbols

• los_angle_of_arrival (float) – Angle-of-arrival for LoS path [radian]. Only used with LoS models. Defaults to \(\pi/4\).

• dtype (tf.DType) – Datatype to use for the output. Should be one of tf.complex64 or tf.complex128. Defaults to tf.complex64.

Output:

cov_mat ([num_ofdm_symbols, num_ofdm_symbols], tf.complex) – Channel time covariance matrix

tdl_freq_cov_mat

sionna.ofdm.tdl_freq_cov_mat(model, subcarrier_spacing, fft_size, delay_spread, dtype=tf.complex64)

Computes the frequency covariance matrix of a TDL channel model.

The channel frequency covariance matrix \(\mathbf{R}^{(f)}\) of a TDL channel model is

\[\mathbf{R}^{(f)}_{u,v} = \sum_{\ell=1}^L P_\ell e^{-j 2 \pi \tau_\ell \Delta_f (u-v)}, 1 \leq u,v \leq M\]

where \(M\) is the FFT size, \(L\) is the number of paths for the selected TDL model, \(P_\ell\) and \(\tau_\ell\) are the average power and delay for the \(\ell^{\text{th}}\) path, respectively, and \(\Delta_f\) is the sub-carrier spacing.

Input:

• model (str) – TDL model for which to return the covariance matrix. Should be one of “A”, “B”, “C”, “D”, or “E”.

• subcarrier_spacing (float) – Sub-carrier spacing [Hz]

• fft_size (float) – FFT size

• delay_spread (float) – Delay spread [s]

• dtype (tf.DType) – Datatype to use for the output. Should be one of tf.complex64 or tf.complex128. Defaults to tf.complex64.

Output:

cov_mat ([fft_size, fft_size], tf.complex) – Channel frequency covariance matrix

Precoding

ZFPrecoder

class sionna.ofdm.ZFPrecoder(resource_grid, stream_management, return_effective_channel=False, dtype=tf.complex64, **kwargs)

Zero-forcing precoding for multi-antenna transmissions.

This layer precodes a tensor containing OFDM resource grids using the zero_forcing_precoder(). For every transmitter, the channels to all intended receivers are gathered into a channel matrix, based on the which the precoding matrix is computed and the input tensor is precoded. The layer also outputs optionally the effective channel after precoding for each stream.

Parameters:

• resource_grid (ResourceGrid) – An instance of ResourceGrid.

• stream_management (StreamManagement) – An instance of StreamManagement.

• return_effective_channel (bool) – Indicates if the effective channel after precoding should be returned.

• dtype (tf.Dtype) – Datatype for internal calculations and the output dtype. Defaults to tf.complex64.

Input:

• (x, h) – Tuple:

• x ([batch_size, num_tx, num_streams_per_tx, num_ofdm_symbols, fft_size], tf.complex) – Tensor containing the resource grid to be precoded.

• h ([batch_size, num_rx, num_rx_ant, num_tx, num_tx_ant, num_ofdm, fft_size], tf.complex) – Tensor containing the channel knowledge based on which the precoding is computed.

Output:

• x_precoded ([batch_size, num_tx, num_tx_ant, num_ofdm_symbols, fft_size], tf.complex) – The precoded resource grids.

• h_eff ([batch_size, num_rx, num_rx_ant, num_tx, num_streams_per_tx, num_ofdm, num_effective_subcarriers], tf.complex) – Only returned if return_effective_channel=True. The effectice channels for all streams after precoding. Can be used to simulate perfect channel state information (CSI) at the receivers. Nulled subcarriers are automatically removed to be compliant with the behavior of a channel estimator.

Note

If you want to use this layer in Graph mode with XLA, i.e., within a function that is decorated with @tf.function(jit_compile=True), you must set sionna.Config.xla_compat=true. See xla_compat.

Equalization

OFDMEqualizer

class sionna.ofdm.OFDMEqualizer(equalizer, resource_grid, stream_management, dtype=tf.complex64, **kwargs)

Layer that wraps a MIMO equalizer for use with the OFDM waveform.

The parameter equalizer is a callable (e.g., a function) that implements a MIMO equalization algorithm for arbitrary batch dimensions.

This class pre-processes the received resource grid y and channel estimate h_hat, and computes for each receiver the noise-plus-interference covariance matrix according to the OFDM and stream configuration provided by the resource_grid and stream_management, which also accounts for the channel estimation error variance err_var. These quantities serve as input to the equalization algorithm that is implemented by the callable equalizer. This layer computes soft-symbol estimates together with effective noise variances for all streams which can, e.g., be used by a Demapper to obtain LLRs.

Note

The callable equalizer must take three inputs:

• y ([…,num_rx_ant], tf.complex) – 1+D tensor containing the received signals.

• h ([…,num_rx_ant,num_streams_per_rx], tf.complex) – 2+D tensor containing the channel matrices.

• s ([…,num_rx_ant,num_rx_ant], tf.complex) – 2+D tensor containing the noise-plus-interference covariance matrices.

It must generate two outputs:

• x_hat ([…,num_streams_per_rx], tf.complex) – 1+D tensor representing the estimated symbol vectors.

• no_eff (tf.float) – Tensor of the same shape as x_hat containing the effective noise variance estimates.

Parameters:

• equalizer (Callable) – Callable object (e.g., a function) that implements a MIMO equalization algorithm for arbitrary batch dimensions

• resource_grid (ResourceGrid) – Instance of ResourceGrid

• stream_management (StreamManagement) – Instance of StreamManagement

• dtype (tf.Dtype) – Datatype for internal calculations and the output dtype. Defaults to tf.complex64.

Input:

• (y, h_hat, err_var, no) – Tuple:

• y ([batch_size, num_rx, num_rx_ant, num_ofdm_symbols, fft_size], tf.complex) – Received OFDM resource grid after cyclic prefix removal and FFT

• h_hat ([batch_size, num_rx, num_rx_ant, num_tx, num_streams_per_tx, num_ofdm_symbols, num_effective_subcarriers], tf.complex) – Channel estimates for all streams from all transmitters

• err_var ([Broadcastable to shape of h_hat], tf.float) – Variance of the channel estimation error

• no ([batch_size, num_rx, num_rx_ant] (or only the first n dims), tf.float) – Variance of the AWGN

Output:

• x_hat ([batch_size, num_tx, num_streams, num_data_symbols], tf.complex) – Estimated symbols

• no_eff ([batch_size, num_tx, num_streams, num_data_symbols], tf.float) – Effective noise variance for each estimated symbol

LMMSEEqualizer

class sionna.ofdm.LMMSEEqualizer(resource_grid, stream_management, whiten_interference=True, dtype=tf.complex64, **kwargs)

LMMSE equalization for OFDM MIMO transmissions.

This layer computes linear minimum mean squared error (LMMSE) equalization for OFDM MIMO transmissions. The OFDM and stream configuration are provided by a ResourceGrid and StreamManagement instance, respectively. The detection algorithm is the lmmse_equalizer(). The layer computes soft-symbol estimates together with effective noise variances for all streams which can, e.g., be used by a Demapper to obtain LLRs.

Parameters:

• resource_grid (ResourceGrid) – Instance of ResourceGrid

• stream_management (StreamManagement) – Instance of StreamManagement

• whiten_interference (bool) – If True (default), the interference is first whitened before equalization. In this case, an alternative expression for the receive filter is used which can be numerically more stable.

• dtype (tf.Dtype) – Datatype for internal calculations and the output dtype. Defaults to tf.complex64.

Input:

• (y, h_hat, err_var, no) – Tuple:

• y ([batch_size, num_rx, num_rx_ant, num_ofdm_symbols, fft_size], tf.complex) – Received OFDM resource grid after cyclic prefix removal and FFT

• h_hat ([batch_size, num_rx, num_rx_ant, num_tx, num_streams_per_tx, num_ofdm_symbols, num_effective_subcarriers], tf.complex) – Channel estimates for all streams from all transmitters

• err_var ([Broadcastable to shape of h_hat], tf.float) – Variance of the channel estimation error

• no ([batch_size, num_rx, num_rx_ant] (or only the first n dims), tf.float) – Variance of the AWGN

Output:

• x_hat ([batch_size, num_tx, num_streams, num_data_symbols], tf.complex) – Estimated symbols

• no_eff ([batch_size, num_tx, num_streams, num_data_symbols], tf.float) – Effective noise variance for each estimated symbol

Note

If you want to use this layer in Graph mode with XLA, i.e., within a function that is decorated with @tf.function(jit_compile=True), you must set sionna.Config.xla_compat=true. See xla_compat.

MFEqualizer

class sionna.ofdm.MFEqualizer(resource_grid, stream_management, dtype=tf.complex64, **kwargs)

MF equalization for OFDM MIMO transmissions.

This layer computes matched filter (MF) equalization for OFDM MIMO transmissions. The OFDM and stream configuration are provided by a ResourceGrid and StreamManagement instance, respectively. The detection algorithm is the mf_equalizer(). The layer computes soft-symbol estimates together with effective noise variances for all streams which can, e.g., be used by a Demapper to obtain LLRs.

Parameters:

• resource_grid (ResourceGrid) – An instance of ResourceGrid.

• stream_management (StreamManagement) – An instance of StreamManagement.

• dtype (tf.Dtype) – Datatype for internal calculations and the output dtype. Defaults to tf.complex64.

Input:

• (y, h_hat, err_var, no) – Tuple:

• y ([batch_size, num_rx, num_rx_ant, num_ofdm_symbols, fft_size], tf.complex) – Received OFDM resource grid after cyclic prefix removal and FFT

• h_hat ([batch_size, num_rx, num_rx_ant, num_tx, num_streams_per_tx, num_ofdm_symbols, num_effective_subcarriers], tf.complex) – Channel estimates for all streams from all transmitters

• err_var ([Broadcastable to shape of h_hat], tf.float) – Variance of the channel estimation error

• no ([batch_size, num_rx, num_rx_ant] (or only the first n dims), tf.float) – Variance of the AWGN

Output:

• x_hat ([batch_size, num_tx, num_streams, num_data_symbols], tf.complex) – Estimated symbols

• no_eff ([batch_size, num_tx, num_streams, num_data_symbols], tf.float) – Effective noise variance for each estimated symbol

Note

If you want to use this layer in Graph mode with XLA, i.e., within a function that is decorated with @tf.function(jit_compile=True), you must set sionna.Config.xla_compat=true. See xla_compat.

ZFEqualizer

class sionna.ofdm.ZFEqualizer(resource_grid, stream_management, dtype=tf.complex64, **kwargs)

ZF equalization for OFDM MIMO transmissions.

This layer computes zero-forcing (ZF) equalization for OFDM MIMO transmissions. The OFDM and stream configuration are provided by a ResourceGrid and StreamManagement instance, respectively. The detection algorithm is the zf_equalizer(). The layer computes soft-symbol estimates together with effective noise variances for all streams which can, e.g., be used by a Demapper to obtain LLRs.

Parameters:

• resource_grid (ResourceGrid) – An instance of ResourceGrid.

• stream_management (StreamManagement) – An instance of StreamManagement.

• dtype (tf.Dtype) – Datatype for internal calculations and the output dtype. Defaults to tf.complex64.

Input:

• (y, h_hat, err_var, no) – Tuple:

• y ([batch_size, num_rx, num_rx_ant, num_ofdm_symbols, fft_size], tf.complex) – Received OFDM resource grid after cyclic prefix removal and FFT

• h_hat ([batch_size, num_rx, num_rx_ant, num_tx, num_streams_per_tx, num_ofdm_symbols, num_effective_subcarriers], tf.complex) – Channel estimates for all streams from all transmitters

• err_var ([Broadcastable to shape of h_hat], tf.float) – Variance of the channel estimation error

• no ([batch_size, num_rx, num_rx_ant] (or only the first n dims), tf.float) – Variance of the AWGN

Output:

• x_hat ([batch_size, num_tx, num_streams, num_data_symbols], tf.complex) – Estimated symbols

• no_eff ([batch_size, num_tx, num_streams, num_data_symbols], tf.float) – Effective noise variance for each estimated symbol

Note

If you want to use this layer in Graph mode with XLA, i.e., within a function that is decorated with @tf.function(jit_compile=True), you must set sionna.Config.xla_compat=true. See xla_compat.

Detection

OFDMDetector

class sionna.ofdm.OFDMDetector(detector, output, resource_grid, stream_management, dtype=tf.complex64, **kwargs)

Layer that wraps a MIMO detector for use with the OFDM waveform.

The parameter detector is a callable (e.g., a function) that implements a MIMO detection algorithm for arbitrary batch dimensions.

This class pre-processes the received resource grid y and channel estimate h_hat, and computes for each receiver the noise-plus-interference covariance matrix according to the OFDM and stream configuration provided by the resource_grid and stream_management, which also accounts for the channel estimation error variance err_var. These quantities serve as input to the detection algorithm that is implemented by detector. Both detection of symbols or bits with either soft- or hard-decisions are supported.

Note

The callable detector must take as input a tuple \((\mathbf{y}, \mathbf{h}, \mathbf{s})\) such that:

• y ([…,num_rx_ant], tf.complex) – 1+D tensor containing the received signals.

• h ([…,num_rx_ant,num_streams_per_rx], tf.complex) – 2+D tensor containing the channel matrices.

• s ([…,num_rx_ant,num_rx_ant], tf.complex) – 2+D tensor containing the noise-plus-interference covariance matrices.

It must generate one of following outputs depending on the value of output:

• b_hat ([…, num_streams_per_rx, num_bits_per_symbol], tf.float) – LLRs or hard-decisions for every bit of every stream, if output equals “bit”.

• x_hat ([…, num_streams_per_rx, num_points], tf.float) or ([…, num_streams_per_rx], tf.int) – Logits or hard-decisions for constellation symbols for every stream, if output equals “symbol”. Hard-decisions correspond to the symbol indices.

Parameters:

• detector (Callable) – Callable object (e.g., a function) that implements a MIMO detection algorithm for arbitrary batch dimensions. Either one of the existing detectors, e.g., LinearDetector, MaximumLikelihoodDetector, or KBestDetector can be used, or a custom detector callable provided that has the same input/output specification.

• output (One of ["bit", "symbol"], str) – Type of output, either bits or symbols

• resource_grid (ResourceGrid) – Instance of ResourceGrid

• stream_management (StreamManagement) – Instance of StreamManagement

• dtype (One of [tf.complex64, tf.complex128] tf.DType (dtype)) – The dtype of y. Defaults to tf.complex64. The output dtype is the corresponding real dtype (tf.float32 or tf.float64).

Input:

• (y, h_hat, err_var, no) – Tuple:

• y ([batch_size, num_rx, num_rx_ant, num_ofdm_symbols, fft_size], tf.complex) – Received OFDM resource grid after cyclic prefix removal and FFT

• h_hat ([batch_size, num_rx, num_rx_ant, num_tx, num_streams_per_tx, num_ofdm_symbols, num_effective_subcarriers], tf.complex) – Channel estimates for all streams from all transmitters

• err_var ([Broadcastable to shape of h_hat], tf.float) – Variance of the channel estimation error

• no ([batch_size, num_rx, num_rx_ant] (or only the first n dims), tf.float) – Variance of the AWGN

Output:

• One of

• [batch_size, num_tx, num_streams, num_data_symbols*num_bits_per_symbol], tf.float – LLRs or hard-decisions for every bit of every stream, if output equals “bit”

• [batch_size, num_tx, num_streams, num_data_symbols, num_points], tf.float or [batch_size, num_tx, num_streams, num_data_symbols], tf.int – Logits or hard-decisions for constellation symbols for every stream, if output equals “symbol”. Hard-decisions correspond to the symbol indices.

OFDMDetectorWithPrior

class sionna.ofdm.OFDMDetectorWithPrior(detector, output, resource_grid, stream_management, constellation_type, num_bits_per_symbol, constellation, dtype=tf.complex64, **kwargs)

Layer that wraps a MIMO detector that assumes prior knowledge of the bits or constellation points is available, for use with the OFDM waveform.

The parameter detector is a callable (e.g., a function) that implements a MIMO detection algorithm with prior for arbitrary batch dimensions.

This class pre-processes the received resource grid y, channel estimate h_hat, and the prior information prior, and computes for each receiver the noise-plus-interference covariance matrix according to the OFDM and stream configuration provided by the resource_grid and stream_management, which also accounts for the channel estimation error variance err_var. These quantities serve as input to the detection algorithm that is implemented by detector. Both detection of symbols or bits with either soft- or hard-decisions are supported.

Note

The callable detector must take as input a tuple \((\mathbf{y}, \mathbf{h}, \mathbf{prior}, \mathbf{s})\) such that:

• y ([…,num_rx_ant], tf.complex) – 1+D tensor containing the received signals.

• h ([…,num_rx_ant,num_streams_per_rx], tf.complex) – 2+D tensor containing the channel matrices.

• prior ([…,num_streams_per_rx,num_bits_per_symbol] or […,num_streams_per_rx,num_points], tf.float) – Prior for the transmitted signals. If output equals “bit”, then LLRs for the transmitted bits are expected. If output equals “symbol”, then logits for the transmitted constellation points are expected.

• s ([…,num_rx_ant,num_rx_ant], tf.complex) – 2+D tensor containing the noise-plus-interference covariance matrices.

It must generate one of the following outputs depending on the value of output:

• b_hat ([…, num_streams_per_rx, num_bits_per_symbol], tf.float) – LLRs or hard-decisions for every bit of every stream, if output equals “bit”.

• x_hat ([…, num_streams_per_rx, num_points], tf.float) or ([…, num_streams_per_rx], tf.int) – Logits or hard-decisions for constellation symbols for every stream, if output equals “symbol”. Hard-decisions correspond to the symbol indices.

Parameters:

• detector (Callable) – Callable object (e.g., a function) that implements a MIMO detection algorithm with prior for arbitrary batch dimensions. Either the existing detector MaximumLikelihoodDetectorWithPrior can be used, or a custom detector callable provided that has the same input/output specification.

• output (One of ["bit", "symbol"], str) – Type of output, either bits or symbols

• resource_grid (ResourceGrid) – Instance of ResourceGrid

• stream_management (StreamManagement) – Instance of StreamManagement

• constellation_type (One of ["qam", "pam", "custom"], str) – For “custom”, an instance of Constellation must be provided.

• num_bits_per_symbol (int) – Number of bits per constellation symbol, e.g., 4 for QAM16. Only required for constellation_type in [“qam”, “pam”].

• constellation (Constellation) – Instance of Constellation or None. In the latter case, constellation_type and num_bits_per_symbol must be provided.

• dtype (One of [tf.complex64, tf.complex128] tf.DType (dtype)) – The dtype of y. Defaults to tf.complex64. The output dtype is the corresponding real dtype (tf.float32 or tf.float64).

Input:

• (y, h_hat, prior, err_var, no) – Tuple:

• y ([batch_size, num_rx, num_rx_ant, num_ofdm_symbols, fft_size], tf.complex) – Received OFDM resource grid after cyclic prefix removal and FFT

• h_hat ([batch_size, num_rx, num_rx_ant, num_tx, num_streams_per_tx, num_ofdm_symbols, num_effective_subcarriers], tf.complex) – Channel estimates for all streams from all transmitters

• prior ([batch_size, num_tx, num_streams, num_data_symbols x num_bits_per_symbol] or [batch_size, num_tx, num_streams, num_data_symbols, num_points], tf.float) – Prior of the transmitted signals. If output equals “bit”, LLRs of the transmitted bits are expected. If output equals “symbol”, logits of the transmitted constellation points are expected.

• err_var ([Broadcastable to shape of h_hat], tf.float) – Variance of the channel estimation error

• no ([batch_size, num_rx, num_rx_ant] (or only the first n dims), tf.float) – Variance of the AWGN

Output:

• One of

• [batch_size, num_tx, num_streams, num_data_symbols*num_bits_per_symbol], tf.float – LLRs or hard-decisions for every bit of every stream, if output equals “bit”.

• [batch_size, num_tx, num_streams, num_data_symbols, num_points], tf.float or [batch_size, num_tx, num_streams, num_data_symbols], tf.int – Logits or hard-decisions for constellation symbols for every stream, if output equals “symbol”. Hard-decisions correspond to the symbol indices.

EPDetector

class sionna.ofdm.EPDetector(output, resource_grid, stream_management, num_bits_per_symbol, hard_out=False, l=10, beta=0.9, dtype=tf.complex64, **kwargs)

This layer wraps the MIMO EP detector for use with the OFDM waveform.

Both detection of symbols or bits with either soft- or hard-decisions are supported. The OFDM and stream configuration are provided by a ResourceGrid and StreamManagement instance, respectively. The actual detector is an instance of EPDetector.

Parameters:

• output (One of ["bit", "symbol"], str) – Type of output, either bits or symbols. Whether soft- or hard-decisions are returned can be configured with the hard_out flag.

• resource_grid (ResourceGrid) – Instance of ResourceGrid

• stream_management (StreamManagement) – Instance of StreamManagement

• num_bits_per_symbol (int) – Number of bits per constellation symbol, e.g., 4 for QAM16. Only required for constellation_type in [“qam”, “pam”].

• hard_out (bool) – If True, the detector computes hard-decided bit values or constellation point indices instead of soft-values. Defaults to False.

• l (int) – Number of iterations. Defaults to 10.

• beta (float) – Parameter \(\beta\in[0,1]\) for update smoothing. Defaults to 0.9.

• dtype (One of [tf.complex64, tf.complex128] tf.DType (dtype)) – Precision used for internal computations. Defaults to tf.complex64. Especially for large MIMO setups, the precision can make a significant performance difference.

Input:

• (y, h_hat, err_var, no) – Tuple:

• y ([batch_size, num_rx, num_rx_ant, num_ofdm_symbols, fft_size], tf.complex) – Received OFDM resource grid after cyclic prefix removal and FFT

• h_hat ([batch_size, num_rx, num_rx_ant, num_tx, num_streams_per_tx, num_ofdm_symbols, num_effective_subcarriers], tf.complex) – Channel estimates for all streams from all transmitters

• err_var ([Broadcastable to shape of h_hat], tf.float) – Variance of the channel estimation error

• no ([batch_size, num_rx, num_rx_ant] (or only the first n dims), tf.float) – Variance of the AWGN

Output:

• One of

• [batch_size, num_tx, num_streams, num_data_symbols*num_bits_per_symbol], tf.float – LLRs or hard-decisions for every bit of every stream, if output equals “bit”.

• [batch_size, num_tx, num_streams, num_data_symbols, num_points], tf.float or [batch_size, num_tx, num_streams, num_data_symbols], tf.int – Logits or hard-decisions for constellation symbols for every stream, if output equals “symbol”. Hard-decisions correspond to the symbol indices.

Note

For numerical stability, we do not recommend to use this function in Graph mode with XLA, i.e., within a function that is decorated with @tf.function(jit_compile=True). However, it is possible to do so by setting sionna.Config.xla_compat=true. See xla_compat.

KBestDetector

class sionna.ofdm.KBestDetector(output, num_streams, k, resource_grid, stream_management, constellation_type=None, num_bits_per_symbol=None, constellation=None, hard_out=False, use_real_rep=False, list2llr=None, dtype=tf.complex64, **kwargs)

This layer wraps the MIMO K-Best detector for use with the OFDM waveform.

Both detection of symbols or bits with either soft- or hard-decisions are supported. The OFDM and stream configuration are provided by a ResourceGrid and StreamManagement instance, respectively. The actual detector is an instance of KBestDetector.

Parameters:

• output (One of ["bit", "symbol"], str) – Type of output, either bits or symbols. Whether soft- or hard-decisions are returned can be configured with the hard_out flag.

• num_streams (tf.int) – Number of transmitted streams

• k (tf.int) – Number of paths to keep. Cannot be larger than the number of constellation points to the power of the number of streams.

• resource_grid (ResourceGrid) – Instance of ResourceGrid

• stream_management (StreamManagement) – Instance of StreamManagement

• constellation_type (One of ["qam", "pam", "custom"], str) – For “custom”, an instance of Constellation must be provided.

• num_bits_per_symbol (int) – Number of bits per constellation symbol, e.g., 4 for QAM16. Only required for constellation_type in [“qam”, “pam”].

• constellation (Constellation) – Instance of Constellation or None. In the latter case, constellation_type and num_bits_per_symbol must be provided.

• hard_out (bool) – If True, the detector computes hard-decided bit values or constellation point indices instead of soft-values. Defaults to False.

• use_real_rep (bool) – If True, the detector use the real-valued equivalent representation of the channel. Note that this only works with a QAM constellation. Defaults to False.

• list2llr (None or instance of List2LLR) – The function to be used to compute LLRs from a list of candidate solutions. If None, the default solution List2LLRSimple is used.

• dtype (One of [tf.complex64, tf.complex128] tf.DType (dtype)) – The dtype of y. Defaults to tf.complex64. The output dtype is the corresponding real dtype (tf.float32 or tf.float64).

Input:

• (y, h_hat, err_var, no) – Tuple:

• y ([batch_size, num_rx, num_rx_ant, num_ofdm_symbols, fft_size], tf.complex) – Received OFDM resource grid after cyclic prefix removal and FFT

• h_hat ([batch_size, num_rx, num_rx_ant, num_tx, num_streams_per_tx, num_ofdm_symbols, num_effective_subcarriers], tf.complex) – Channel estimates for all streams from all transmitters

• err_var ([Broadcastable to shape of h_hat], tf.float) – Variance of the channel estimation error

• no ([batch_size, num_rx, num_rx_ant] (or only the first n dims), tf.float) – Variance of the AWGN

Output:

• One of

• [batch_size, num_tx, num_streams, num_data_symbols*num_bits_per_symbol], tf.float – LLRs or hard-decisions for every bit of every stream, if output equals “bit”.

• [batch_size, num_tx, num_streams, num_data_symbols, num_points], tf.float or [batch_size, num_tx, num_streams, num_data_symbols], tf.int – Logits or hard-decisions for constellation symbols for every stream, if output equals “symbol”. Hard-decisions correspond to the symbol indices.

Note

If you want to use this layer in Graph mode with XLA, i.e., within a function that is decorated with @tf.function(jit_compile=True), you must set sionna.Config.xla_compat=true. See xla_compat.

LinearDetector

class sionna.ofdm.LinearDetector(equalizer, output, demapping_method, resource_grid, stream_management, constellation_type=None, num_bits_per_symbol=None, constellation=None, hard_out=False, dtype=tf.complex64, **kwargs)

This layer wraps a MIMO linear equalizer and a Demapper for use with the OFDM waveform.

Both detection of symbols or bits with either soft- or hard-decisions are supported. The OFDM and stream configuration are provided by a ResourceGrid and StreamManagement instance, respectively. The actual detector is an instance of LinearDetector.

Parameters:

• equalizer (str, one of ["lmmse", "zf", "mf"], or an equalizer function) – Equalizer to be used. Either one of the existing equalizers, e.g., lmmse_equalizer(), zf_equalizer(), or mf_equalizer() can be used, or a custom equalizer function provided that has the same input/output specification.

• output (One of ["bit", "symbol"], str) – Type of output, either bits or symbols. Whether soft- or hard-decisions are returned can be configured with the hard_out flag.

• demapping_method (One of ["app", "maxlog"], str) – Demapping method used

• resource_grid (ResourceGrid) – Instance of ResourceGrid

• stream_management (StreamManagement) – Instance of StreamManagement

• constellation_type (One of ["qam", "pam", "custom"], str) – For “custom”, an instance of Constellation must be provided.

• num_bits_per_symbol (int) – Number of bits per constellation symbol, e.g., 4 for QAM16. Only required for constellation_type in [“qam”, “pam”].

• constellation (Constellation) – Instance of Constellation or None. In the latter case, constellation_type and num_bits_per_symbol must be provided.

• hard_out (bool) – If True, the detector computes hard-decided bit values or constellation point indices instead of soft-values. Defaults to False.

• dtype (One of [tf.complex64, tf.complex128] tf.DType (dtype)) – The dtype of y. Defaults to tf.complex64. The output dtype is the corresponding real dtype (tf.float32 or tf.float64).

Input:

• (y, h_hat, err_var, no) – Tuple:

• y ([batch_size, num_rx, num_rx_ant, num_ofdm_symbols, fft_size], tf.complex) – Received OFDM resource grid after cyclic prefix removal and FFT

• h_hat ([batch_size, num_rx, num_rx_ant, num_tx, num_streams_per_tx, num_ofdm_symbols, num_effective_subcarriers], tf.complex) – Channel estimates for all streams from all transmitters

• err_var ([Broadcastable to shape of h_hat], tf.float) – Variance of the channel estimation error

• no ([batch_size, num_rx, num_rx_ant] (or only the first n dims), tf.float) – Variance of the AWGN

Output:

• One of

• [batch_size, num_tx, num_streams, num_data_symbols*num_bits_per_symbol], tf.float – LLRs or hard-decisions for every bit of every stream, if output equals “bit”.

• [batch_size, num_tx, num_streams, num_data_symbols, num_points], tf.float or [batch_size, num_tx, num_streams, num_data_symbols], tf.int – Logits or hard-decisions for constellation symbols for every stream, if output equals “symbol”. Hard-decisions correspond to the symbol indices.

Note

If you want to use this layer in Graph mode with XLA, i.e., within a function that is decorated with @tf.function(jit_compile=True), you must set sionna.Config.xla_compat=true. See xla_compat.

MaximumLikelihoodDetector

class sionna.ofdm.MaximumLikelihoodDetector(output, demapping_method, resource_grid, stream_management, constellation_type=None, num_bits_per_symbol=None, constellation=None, hard_out=False, dtype=tf.complex64, **kwargs)

Maximum-likelihood (ML) detection for OFDM MIMO transmissions.

This layer implements maximum-likelihood (ML) detection for OFDM MIMO transmissions. Both ML detection of symbols or bits with either soft- or hard-decisions are supported. The OFDM and stream configuration are provided by a ResourceGrid and StreamManagement instance, respectively. The actual detector is an instance of MaximumLikelihoodDetector.

Parameters:

• output (One of ["bit", "symbol"], str) – Type of output, either bits or symbols. Whether soft- or hard-decisions are returned can be configured with the hard_out flag.

• demapping_method (One of ["app", "maxlog"], str) – Demapping method used

• resource_grid (ResourceGrid) – Instance of ResourceGrid

• stream_management (StreamManagement) – Instance of StreamManagement

• constellation_type (One of ["qam", "pam", "custom"], str) – For “custom”, an instance of Constellation must be provided.

• num_bits_per_symbol (int) – Number of bits per constellation symbol, e.g., 4 for QAM16. Only required for constellation_type in [“qam”, “pam”].

• constellation (Constellation) – Instance of Constellation or None. In the latter case, constellation_type and num_bits_per_symbol must be provided.

• hard_out (bool) – If True, the detector computes hard-decided bit values or constellation point indices instead of soft-values. Defaults to False.

• dtype (One of [tf.complex64, tf.complex128] tf.DType (dtype)) – The dtype of y. Defaults to tf.complex64. The output dtype is the corresponding real dtype (tf.float32 or tf.float64).

Input:

• (y, h_hat, err_var, no) – Tuple:

• y ([batch_size, num_rx, num_rx_ant, num_ofdm_symbols, fft_size], tf.complex) – Received OFDM resource grid after cyclic prefix removal and FFT

• h_hat ([batch_size, num_rx, num_rx_ant, num_tx, num_streams_per_tx, num_ofdm_symbols, num_effective_subcarriers], tf.complex) – Channel estimates for all streams from all transmitters

• err_var ([Broadcastable to shape of h_hat], tf.float) – Variance of the channel estimation error

• no ([batch_size, num_rx, num_rx_ant] (or only the first n dims), tf.float) – Variance of the AWGN noise

Output:

• One of

• [batch_size, num_tx, num_streams, num_data_symbols*num_bits_per_symbol], tf.float – LLRs or hard-decisions for every bit of every stream, if output equals “bit”.

• [batch_size, num_tx, num_streams, num_data_symbols, num_points], tf.float or [batch_size, num_tx, num_streams, num_data_symbols], tf.int – Logits or hard-decisions for constellation symbols for every stream, if output equals “symbol”. Hard-decisions correspond to the symbol indices.

Note

If you want to use this layer in Graph mode with XLA, i.e., within a function that is decorated with @tf.function(jit_compile=True), you must set sionna.Config.xla_compat=true. See xla_compat.

MaximumLikelihoodDetectorWithPrior

class sionna.ofdm.MaximumLikelihoodDetectorWithPrior(output, demapping_method, resource_grid, stream_management, constellation_type=None, num_bits_per_symbol=None, constellation=None, hard_out=False, dtype=tf.complex64, **kwargs)

Maximum-likelihood (ML) detection for OFDM MIMO transmissions, assuming prior knowledge of the bits or constellation points is available.

This layer implements maximum-likelihood (ML) detection for OFDM MIMO transmissions assuming prior knowledge on the transmitted data is available. Both ML detection of symbols or bits with either soft- or hard-decisions are supported. The OFDM and stream configuration are provided by a ResourceGrid and StreamManagement instance, respectively. The actual detector is an instance of MaximumLikelihoodDetectorWithPrior.

Parameters:

• output (One of ["bit", "symbol"], str) – Type of output, either bits or symbols. Whether soft- or hard-decisions are returned can be configured with the hard_out flag.

• demapping_method (One of ["app", "maxlog"], str) – Demapping method used

• resource_grid (ResourceGrid) – Instance of ResourceGrid

• stream_management (StreamManagement) – Instance of StreamManagement

• constellation_type (One of ["qam", "pam", "custom"], str) – For “custom”, an instance of Constellation must be provided.

• num_bits_per_symbol (int) – Number of bits per constellation symbol, e.g., 4 for QAM16. Only required for constellation_type in [“qam”, “pam”].

• constellation (Constellation) – Instance of Constellation or None. In the latter case, constellation_type and num_bits_per_symbol must be provided.

• hard_out (bool) – If True, the detector computes hard-decided bit values or constellation point indices instead of soft-values. Defaults to False.

• dtype (One of [tf.complex64, tf.complex128] tf.DType (dtype)) – The dtype of y. Defaults to tf.complex64. The output dtype is the corresponding real dtype (tf.float32 or tf.float64).

Input:

• (y, h_hat, prior, err_var, no) – Tuple:

• y ([batch_size, num_rx, num_rx_ant, num_ofdm_symbols, fft_size], tf.complex) – Received OFDM resource grid after cyclic prefix removal and FFT

• h_hat ([batch_size, num_rx, num_rx_ant, num_tx, num_streams_per_tx, num_ofdm_symbols, num_effective_subcarriers], tf.complex) – Channel estimates for all streams from all transmitters

• prior ([batch_size, num_tx, num_streams, num_data_symbols x num_bits_per_symbol] or [batch_size, num_tx, num_streams, num_data_symbols, num_points], tf.float) – Prior of the transmitted signals. If output equals “bit”, LLRs of the transmitted bits are expected. If output equals “symbol”, logits of the transmitted constellation points are expected.

• err_var ([Broadcastable to shape of h_hat], tf.float) – Variance of the channel estimation error

• no ([batch_size, num_rx, num_rx_ant] (or only the first n dims), tf.float) – Variance of the AWGN noise

Output:

• One of

• [batch_size, num_tx, num_streams, num_data_symbols*num_bits_per_symbol], tf.float – LLRs or hard-decisions for every bit of every stream, if output equals “bit”.

• [batch_size, num_tx, num_streams, num_data_symbols, num_points], tf.float or [batch_size, num_tx, num_streams, num_data_symbols], tf.int – Logits or hard-decisions for constellation symbols for every stream, if output equals “symbol”. Hard-decisions correspond to the symbol indices.

Note

If you want to use this layer in Graph mode with XLA, i.e., within a function that is decorated with @tf.function(jit_compile=True), you must set sionna.Config.xla_compat=true. See xla_compat.

MMSEPICDetector

class sionna.ofdm.MMSEPICDetector(output, resource_grid, stream_management, demapping_method='maxlog', num_iter=1, constellation_type=None, num_bits_per_symbol=None, constellation=None, hard_out=False, dtype=tf.complex64, **kwargs)

This layer wraps the MIMO MMSE PIC detector for use with the OFDM waveform.

Both detection of symbols or bits with either soft- or hard-decisions are supported. The OFDM and stream configuration are provided by a ResourceGrid and StreamManagement instance, respectively. The actual detector is an instance of MMSEPICDetector.

Parameters:

• output (One of ["bit", "symbol"], str) – Type of output, either bits or symbols. Whether soft- or hard-decisions are returned can be configured with the hard_out flag.

• resource_grid (ResourceGrid) – Instance of ResourceGrid

• stream_management (StreamManagement) – Instance of StreamManagement

• demapping_method (One of ["app", "maxlog"], str) – The demapping method used. Defaults to “maxlog”.

• num_iter (int) – Number of MMSE PIC iterations. Defaults to 1.

• constellation_type (One of ["qam", "pam", "custom"], str) – For “custom”, an instance of Constellation must be provided.

• num_bits_per_symbol (int) – The number of bits per constellation symbol, e.g., 4 for QAM16. Only required for constellation_type in [“qam”, “pam”].

• constellation (Constellation) – An instance of Constellation or None. In the latter case, constellation_type and num_bits_per_symbol must be provided.

• hard_out (bool) – If True, the detector computes hard-decided bit values or constellation point indices instead of soft-values. Defaults to False.

• dtype (One of [tf.complex64, tf.complex128] tf.DType (dtype)) – Precision used for internal computations. Defaults to tf.complex64. Especially for large MIMO setups, the precision can make a significant performance difference.

Input:

• (y, h_hat, prior, err_var, no) – Tuple:

• y ([batch_size, num_rx, num_rx_ant, num_ofdm_symbols, fft_size], tf.complex) – Received OFDM resource grid after cyclic prefix removal and FFT

• h_hat ([batch_size, num_rx, num_rx_ant, num_tx, num_streams_per_tx, num_ofdm_symbols, num_effective_subcarriers], tf.complex) – Channel estimates for all streams from all transmitters

• prior ([batch_size, num_tx, num_streams, num_data_symbols x num_bits_per_symbol] or [batch_size, num_tx, num_streams, num_data_symbols, num_points], tf.float) – Prior of the transmitted signals. If output equals “bit”, LLRs of the transmitted bits are expected. If output equals “symbol”, logits of the transmitted constellation points are expected.

• err_var ([Broadcastable to shape of h_hat], tf.float) – Variance of the channel estimation error

• no ([batch_size, num_rx, num_rx_ant] (or only the first n dims), tf.float) – Variance of the AWGN

Output:

• One of

• [batch_size, num_tx, num_streams, num_data_symbols*num_bits_per_symbol], tf.float – LLRs or hard-decisions for every bit of every stream, if output equals “bit”.

• [batch_size, num_tx, num_streams, num_data_symbols, num_points], tf.float or [batch_size, num_tx, num_streams, num_data_symbols], tf.int – Logits or hard-decisions for constellation symbols for every stream, if output equals “symbol”. Hard-decisions correspond to the symbol indices.

Note

For numerical stability, we do not recommend to use this function in Graph mode with XLA, i.e., within a function that is decorated with @tf.function(jit_compile=True). However, it is possible to do so by setting sionna.Config.xla_compat=true. See xla_compat.