Signal
This module contains classes and functions for filtering (pulse shaping), windowing, and up- and downsampling. The following figure shows the different components that can be implemented using this module.
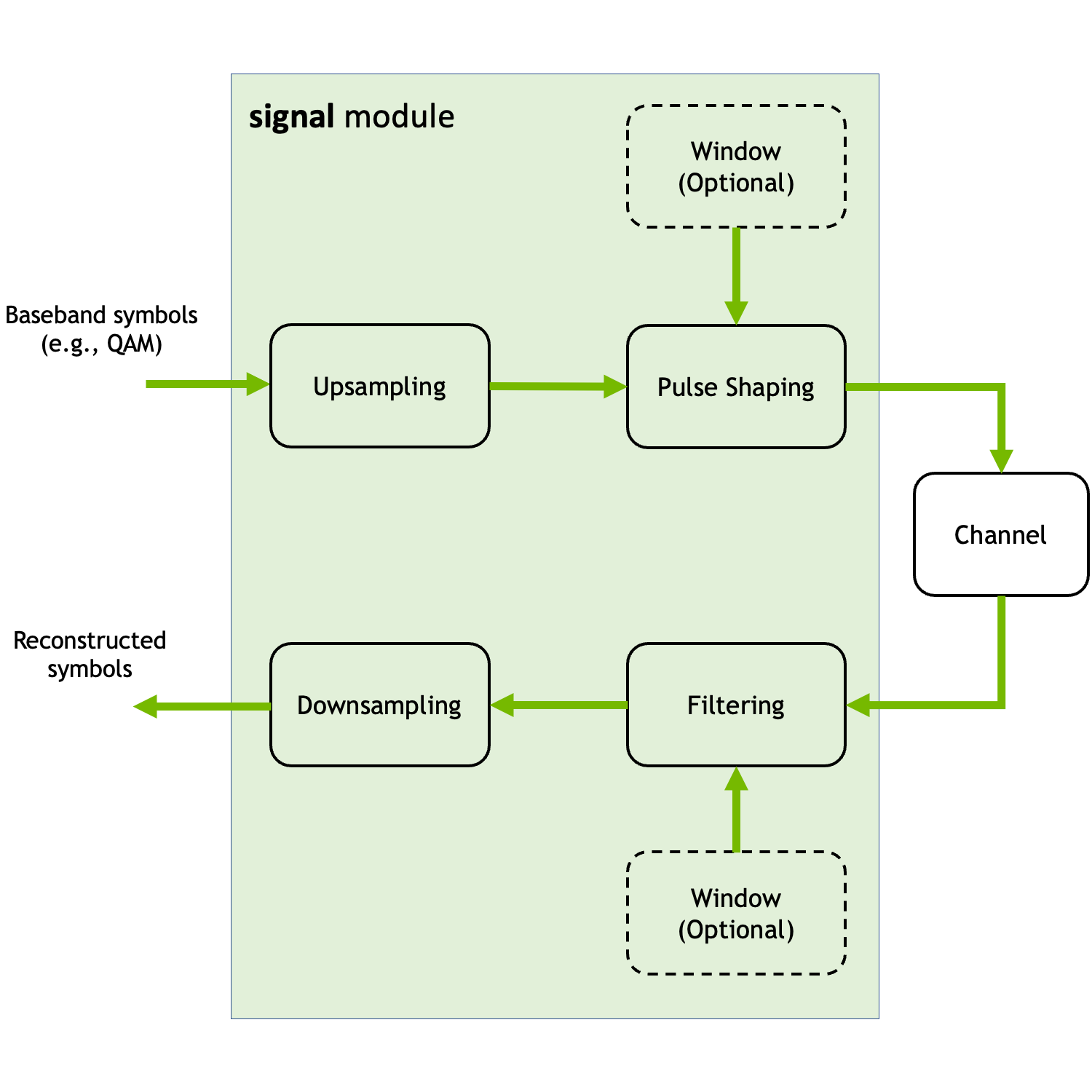
This module also contains utility functions for computing the (inverse) discrete Fourier transform (FFT/IFFT), and for empirically computing the power spectral density (PSD) and adjacent channel leakage ratio (ACLR) of a signal.
The following code snippet shows how to filter a sequence of QAM baseband symbols using a root-raised-cosine filter with a Hann window:
# Create batch of QAM-16 sequences
batch_size = 128
num_symbols = 1000
num_bits_per_symbol = 4
x = QAMSource(num_bits_per_symbol)([batch_size, num_symbols])
# Create a root-raised-cosine filter with Hann windowing
beta = 0.22 # Roll-off factor
span_in_symbols = 32 # Filter span in symbols
samples_per_symbol = 4 # Number of samples per symbol, i.e., the oversampling factor
rrcf_hann = RootRaisedCosineFilter(span_in_symbols, samples_per_symbol, beta, window="hann")
# Create instance of the Upsampling layer
us = Upsampling(samples_per_symbol)
# Upsample the baseband x
x_us = us(x)
# Filter the upsampled sequence
x_rrcf = rrcf_hann(x_us)
On the receiver side, one would recover the baseband symbols as follows:
# Instantiate a downsampling layer
ds = Downsampling(samples_per_symbol, rrcf_hann.length-1, num_symbols)
# Apply the matched filter
x_mf = rrcf_hann(x_rrcf)
# Recover the transmitted symbol sequence
x_hat = ds(x_mf)
Filters
SincFilter
- class sionna.signal.SincFilter(span_in_symbols, samples_per_symbol, window=None, normalize=True, trainable=False, dtype=tf.float32, **kwargs)[source]
Layer for applying a sinc filter of
lengthK to an inputxof length N.The sinc filter is defined by
\[h(t) = \frac{1}{T}\text{sinc}\left(\frac{t}{T}\right)\]where \(T\) the symbol duration.
The filter length K is equal to the filter span in symbols (
span_in_symbols) multiplied by the oversampling factor (samples_per_symbol). If this product is even, a value of one will be added.The filter is applied through discrete convolution.
An optional windowing function
windowcan be applied to the filter.The dtype of the output is tf.float if both
xand the filter coefficients have dtype tf.float. Otherwise, the dtype of the output is tf.complex.Three padding modes are available for applying the filter:
“full” (default): Returns the convolution at each point of overlap between
xand the filter. The length of the output is N + K - 1. Zero-padding of the inputxis performed to compute the convolution at the borders.“same”: Returns an output of the same length as the input
x. The convolution is computed such that the coefficients of the inputxare centered on the coefficient of the filter with index (K-1)/2. Zero-padding of the input signal is performed to compute the convolution at the borders.“valid”: Returns the convolution only at points where
xand the filter completely overlap. The length of the output is N - K + 1.
- Parameters:
span_in_symbols (int) – Filter span as measured by the number of symbols.
samples_per_symbol (int) – Number of samples per symbol, i.e., the oversampling factor.
window (Window or string (["hann", "hamming", "blackman"])) – Instance of
Windowthat is applied to the filter coefficients. Alternatively, a string indicating the window name can be provided. In this case, the chosen window will be instantiated with the default parameters. Custom windows must be provided as instance.normalize (bool) – If True, the filter is normalized to have unit power. Defaults to True.
trainable (bool) – If True, the filter coefficients are trainable variables. Defaults to False.
dtype (tf.DType) – The dtype of the filter coefficients. Defaults to tf.float32.
- Input:
x ([…, N], tf.complex or tf.float) – The input to which the filter is applied. The filter is applied along the last dimension.
padding (string ([“full”, “valid”, “same”])) – Padding mode for convolving
xand the filter. Must be one of “full”, “valid”, or “same”. Case insensitive. Defaults to “full”.conjugate (bool) – If True, the complex conjugate of the filter is applied. Defaults to False.
- Output:
y ([…,M], tf.complex or tf.float) – Filtered input. It is tf.float only if both
xand the filter are tf.float. It is tf.complex otherwise. The length M depends on thepadding.
- property aclr
ACLR of the filter
This ACLR corresponds to what one would obtain from using this filter as pulse shaping filter on an i.i.d. sequence of symbols. The in-band is assumed to range from [-0.5, 0.5] in normalized frequency.
- property coefficients
The filter coefficients (after normalization)
- property length
The filter length in samples
- property normalize
True if the filter is normalized to have unit power. False otherwise.
- property sampling_times
Sampling times in multiples of the symbol duration
- show(response='impulse', scale='lin')
Plot the impulse or magnitude response
Plots the impulse response (time domain) or magnitude response (frequency domain) of the filter.
For the computation of the magnitude response, a minimum DFT size of 1024 is assumed which is obtained through zero padding of the filter coefficients in the time domain.
- Input:
response (str, one of [“impulse”, “magnitude”]) – The desired response type. Defaults to “impulse”
scale (str, one of [“lin”, “db”]) – The y-scale of the magnitude response. Can be “lin” (i.e., linear) or “db” (, i.e., Decibel). Defaults to “lin”.
- property trainable
True if the filter coefficients are trainable. False otherwise.
- property window
The window function that is applied to the filter coefficients. None if no window is applied.
RaisedCosineFilter
- class sionna.signal.RaisedCosineFilter(span_in_symbols, samples_per_symbol, beta, window=None, normalize=True, trainable=False, dtype=tf.float32, **kwargs)[source]
Layer for applying a raised-cosine filter of
lengthK to an inputxof length N.The raised-cosine filter is defined by
\[\begin{split}h(t) = \begin{cases} \frac{\pi}{4T} \text{sinc}\left(\frac{1}{2\beta}\right), & \text { if }t = \pm \frac{T}{2\beta}\\ \frac{1}{T}\text{sinc}\left(\frac{t}{T}\right)\frac{\cos\left(\frac{\pi\beta t}{T}\right)}{1-\left(\frac{2\beta t}{T}\right)^2}, & \text{otherwise} \end{cases}\end{split}\]where \(\beta\) is the roll-off factor and \(T\) the symbol duration.
The filter length K is equal to the filter span in symbols (
span_in_symbols) multiplied by the oversampling factor (samples_per_symbol). If this product is even, a value of one will be added.The filter is applied through discrete convolution.
An optional windowing function
windowcan be applied to the filter.The dtype of the output is tf.float if both
xand the filter coefficients have dtype tf.float. Otherwise, the dtype of the output is tf.complex.Three padding modes are available for applying the filter:
“full” (default): Returns the convolution at each point of overlap between
xand the filter. The length of the output is N + K - 1. Zero-padding of the inputxis performed to compute the convolution at the borders.“same”: Returns an output of the same length as the input
x. The convolution is computed such that the coefficients of the inputxare centered on the coefficient of the filter with index (K-1)/2. Zero-padding of the input signal is performed to compute the convolution at the borders.“valid”: Returns the convolution only at points where
xand the filter completely overlap. The length of the output is N - K + 1.
- Parameters:
span_in_symbols (int) – Filter span as measured by the number of symbols.
samples_per_symbol (int) – Number of samples per symbol, i.e., the oversampling factor.
beta (float) – Roll-off factor. Must be in the range \([0,1]\).
window (Window or string (["hann", "hamming", "blackman"])) – Instance of
Windowthat is applied to the filter coefficients. Alternatively, a string indicating the window name can be provided. In this case, the chosen window will be instantiated with the default parameters. Custom windows must be provided as instance.normalize (bool) – If True, the filter is normalized to have unit power. Defaults to True.
trainable (bool) – If True, the filter coefficients are trainable variables. Defaults to False.
dtype (tf.DType) – The dtype of the filter coefficients. Defaults to tf.float32.
- Input:
x ([…, N], tf.complex or tf.float) – The input to which the filter is applied. The filter is applied along the last dimension.
padding (string ([“full”, “valid”, “same”])) – Padding mode for convolving
xand the filter. Must be one of “full”, “valid”, or “same”. Defaults to “full”.conjugate (bool) – If True, the complex conjugate of the filter is applied. Defaults to False.
- Output:
y ([…,M], tf.complex or tf.float) – Filtered input. It is tf.float only if both
xand the filter are tf.float. It is tf.complex otherwise. The length M depends on thepadding.
- property aclr
ACLR of the filter
This ACLR corresponds to what one would obtain from using this filter as pulse shaping filter on an i.i.d. sequence of symbols. The in-band is assumed to range from [-0.5, 0.5] in normalized frequency.
- property beta
Roll-off factor
- property coefficients
The filter coefficients (after normalization)
- property length
The filter length in samples
- property normalize
True if the filter is normalized to have unit power. False otherwise.
- property sampling_times
Sampling times in multiples of the symbol duration
- show(response='impulse', scale='lin')
Plot the impulse or magnitude response
Plots the impulse response (time domain) or magnitude response (frequency domain) of the filter.
For the computation of the magnitude response, a minimum DFT size of 1024 is assumed which is obtained through zero padding of the filter coefficients in the time domain.
- Input:
response (str, one of [“impulse”, “magnitude”]) – The desired response type. Defaults to “impulse”
scale (str, one of [“lin”, “db”]) – The y-scale of the magnitude response. Can be “lin” (i.e., linear) or “db” (, i.e., Decibel). Defaults to “lin”.
- property trainable
True if the filter coefficients are trainable. False otherwise.
- property window
The window function that is applied to the filter coefficients. None if no window is applied.
RootRaisedCosineFilter
- class sionna.signal.RootRaisedCosineFilter(span_in_symbols, samples_per_symbol, beta, window=None, normalize=True, trainable=False, dtype=tf.float32, **kwargs)[source]
Layer for applying a root-raised-cosine filter of
lengthK to an inputxof length N.The root-raised-cosine filter is defined by
\[\begin{split}h(t) = \begin{cases} \frac{1}{T} \left(1 + \beta\left(\frac{4}{\pi}-1\right) \right), & \text { if }t = 0\\ \frac{\beta}{T\sqrt{2}} \left[ \left(1+\frac{2}{\pi}\right)\sin\left(\frac{\pi}{4\beta}\right) + \left(1-\frac{2}{\pi}\right)\cos\left(\frac{\pi}{4\beta}\right) \right], & \text { if }t = \pm\frac{T}{4\beta} \\ \frac{1}{T} \frac{\sin\left(\pi\frac{t}{T}(1-\beta)\right) + 4\beta\frac{t}{T}\cos\left(\pi\frac{t}{T}(1+\beta)\right)}{\pi\frac{t}{T}\left(1-\left(4\beta\frac{t}{T}\right)^2\right)}, & \text { otherwise} \end{cases}\end{split}\]where \(\beta\) is the roll-off factor and \(T\) the symbol duration.
The filter length K is equal to the filter span in symbols (
span_in_symbols) multiplied by the oversampling factor (samples_per_symbol). If this product is even, a value of one will be added.The filter is applied through discrete convolution.
An optional windowing function
windowcan be applied to the filter.The dtype of the output is tf.float if both
xand the filter coefficients have dtype tf.float. Otherwise, the dtype of the output is tf.complex.Three padding modes are available for applying the filter:
“full” (default): Returns the convolution at each point of overlap between
xand the filter. The length of the output is N + K - 1. Zero-padding of the inputxis performed to compute the convolution at the borders.“same”: Returns an output of the same length as the input
x. The convolution is computed such that the coefficients of the inputxare centered on the coefficient of the filter with index (K-1)/2. Zero-padding of the input signal is performed to compute the convolution at the borders.“valid”: Returns the convolution only at points where
xand the filter completely overlap. The length of the output is N - K + 1.
- Parameters:
span_in_symbols (int) – Filter span as measured by the number of symbols.
samples_per_symbol (int) – Number of samples per symbol, i.e., the oversampling factor.
beta (float) – Roll-off factor. Must be in the range \([0,1]\).
window (Window or string (["hann", "hamming", "blackman"])) – Instance of
Windowthat is applied to the filter coefficients. Alternatively, a string indicating the window name can be provided. In this case, the chosen window will be instantiated with the default parameters. Custom windows must be provided as instance.normalize (bool) – If True, the filter is normalized to have unit power. Defaults to True.
trainable (bool) – If True, the filter coefficients are trainable variables. Defaults to False.
dtype (tf.DType) – The dtype of the filter coefficients. Defaults to tf.float32.
- Input:
x ([…, N], tf.complex or tf.float) – The input to which the filter is applied. The filter is applied along the last dimension.
padding (string ([“full”, “valid”, “same”])) – Padding mode for convolving
xand the filter. Must be one of “full”, “valid”, or “same”. Case insensitive. Defaults to “full”.conjugate (bool) – If True, the complex conjugate of the filter is applied. Defaults to False.
- Output:
y ([…,M], tf.complex or tf.float) – Filtered input. It is tf.float only if both
xand the filter are tf.float. It is tf.complex otherwise. The length M depends on thepadding.
- property aclr
ACLR of the filter
This ACLR corresponds to what one would obtain from using this filter as pulse shaping filter on an i.i.d. sequence of symbols. The in-band is assumed to range from [-0.5, 0.5] in normalized frequency.
- property beta
Roll-off factor
- property coefficients
The filter coefficients (after normalization)
- property length
The filter length in samples
- property normalize
True if the filter is normalized to have unit power. False otherwise.
- property sampling_times
Sampling times in multiples of the symbol duration
- show(response='impulse', scale='lin')
Plot the impulse or magnitude response
Plots the impulse response (time domain) or magnitude response (frequency domain) of the filter.
For the computation of the magnitude response, a minimum DFT size of 1024 is assumed which is obtained through zero padding of the filter coefficients in the time domain.
- Input:
response (str, one of [“impulse”, “magnitude”]) – The desired response type. Defaults to “impulse”
scale (str, one of [“lin”, “db”]) – The y-scale of the magnitude response. Can be “lin” (i.e., linear) or “db” (, i.e., Decibel). Defaults to “lin”.
- property trainable
True if the filter coefficients are trainable. False otherwise.
- property window
The window function that is applied to the filter coefficients. None if no window is applied.
CustomFilter
- class sionna.signal.CustomFilter(span_in_symbols=None, samples_per_symbol=None, coefficients=None, window=None, normalize=True, trainable=False, dtype=tf.float32, **kwargs)[source]
Layer for applying a custom filter of
lengthK to an inputxof length N.The filter length K is equal to the filter span in symbols (
span_in_symbols) multiplied by the oversampling factor (samples_per_symbol). If this product is even, a value of one will be added.The filter is applied through discrete convolution.
An optional windowing function
windowcan be applied to the filter.The dtype of the output is tf.float if both
xand the filter coefficients have dtype tf.float. Otherwise, the dtype of the output is tf.complex.Three padding modes are available for applying the filter:
“full” (default): Returns the convolution at each point of overlap between
xand the filter. The length of the output is N + K - 1. Zero-padding of the inputxis performed to compute the convolution at the borders.“same”: Returns an output of the same length as the input
x. The convolution is computed such that the coefficients of the inputxare centered on the coefficient of the filter with index (K-1)/2. Zero-padding of the input signal is performed to compute the convolution at the borders.“valid”: Returns the convolution only at points where
xand the filter completely overlap. The length of the output is N - K + 1.
- Parameters:
span_in_symbols (int) – Filter span as measured by the number of symbols. Only needs to be provided if
coefficientsis None.samples_per_symbol (int) – Number of samples per symbol, i.e., the oversampling factor. Must always be provided.
coefficients ([K], tf.float or tf.complex) – Optional filter coefficients. If set to None, then a random filter of K is generated by sampling a Gaussian distribution. Defaults to None.
window (Window or string (["hann", "hamming", "blackman"])) – Instance of
Windowthat is applied to the filter coefficients. Alternatively, a string indicating the window name can be provided. In this case, the chosen window will be instantiated with the default parameters. Custom windows must be provided as instance.normalize (bool) – If True, the filter is normalized to have unit power. Defaults to True.
trainable (bool) – If True, the filter coefficients are trainable variables. Defaults to False.
dtype (tf.DType) – The dtype of the filter coefficients. Defaults to tf.float32.
- Input:
x ([…, N], tf.complex or tf.float) – The input to which the filter is applied. The filter is applied along the last dimension.
padding (string ([“full”, “valid”, “same”])) – Padding mode for convolving
xand the filter. Must be one of “full”, “valid”, or “same”. Case insensitive. Defaults to “full”.conjugate (bool) – If True, the complex conjugate of the filter is applied. Defaults to False.
- Output:
y ([…,M], tf.complex or tf.float) – Filtered input. It is tf.float only if both
xand the filter are tf.float. It is tf.complex otherwise. The length M depends on thepadding.
- property aclr
ACLR of the filter
This ACLR corresponds to what one would obtain from using this filter as pulse shaping filter on an i.i.d. sequence of symbols. The in-band is assumed to range from [-0.5, 0.5] in normalized frequency.
- property coefficients
The filter coefficients (after normalization)
- property length
The filter length in samples
- property normalize
True if the filter is normalized to have unit power. False otherwise.
- property sampling_times
Sampling times in multiples of the symbol duration
- show(response='impulse', scale='lin')
Plot the impulse or magnitude response
Plots the impulse response (time domain) or magnitude response (frequency domain) of the filter.
For the computation of the magnitude response, a minimum DFT size of 1024 is assumed which is obtained through zero padding of the filter coefficients in the time domain.
- Input:
response (str, one of [“impulse”, “magnitude”]) – The desired response type. Defaults to “impulse”
scale (str, one of [“lin”, “db”]) – The y-scale of the magnitude response. Can be “lin” (i.e., linear) or “db” (, i.e., Decibel). Defaults to “lin”.
- property trainable
True if the filter coefficients are trainable. False otherwise.
- property window
The window function that is applied to the filter coefficients. None if no window is applied.
Filter
- class sionna.signal.Filter(span_in_symbols, samples_per_symbol, window=None, normalize=True, trainable=False, dtype=tf.float32, **kwargs)[source]
This is an abtract class for defining a filter of
lengthK which can be applied to an inputxof length N.The filter length K is equal to the filter span in symbols (
span_in_symbols) multiplied by the oversampling factor (samples_per_symbol). If this product is even, a value of one will be added.The filter is applied through discrete convolution.
An optional windowing function
windowcan be applied to the filter.The dtype of the output is tf.float if both
xand the filter coefficients have dtype tf.float. Otherwise, the dtype of the output is tf.complex.Three padding modes are available for applying the filter:
“full” (default): Returns the convolution at each point of overlap between
xand the filter. The length of the output is N + K - 1. Zero-padding of the inputxis performed to compute the convolution at the borders.“same”: Returns an output of the same length as the input
x. The convolution is computed such that the coefficients of the inputxare centered on the coefficient of the filter with index (K-1)/2. Zero-padding of the input signal is performed to compute the convolution at the borders.“valid”: Returns the convolution only at points where
xand the filter completely overlap. The length of the output is N - K + 1.
- Parameters:
span_in_symbols (int) – Filter span as measured by the number of symbols.
samples_per_symbol (int) – Number of samples per symbol, i.e., the oversampling factor.
window (Window or string (["hann", "hamming", "blackman"])) – Instance of
Windowthat is applied to the filter coefficients. Alternatively, a string indicating the window name can be provided. In this case, the chosen window will be instantiated with the default parameters. Custom windows must be provided as instance.normalize (bool) – If True, the filter is normalized to have unit power. Defaults to True.
trainable (bool) – If True, the filter coefficients are trainable. Defaults to False.
dtype (tf.DType) – The dtype of the filter coefficients. Defaults to tf.float32.
- Input:
x ([…, N], tf.complex or tf.float) – The input to which the filter is applied. The filter is applied along the last dimension.
padding (string ([“full”, “valid”, “same”])) – Padding mode for convolving
xand the filter. Must be one of “full”, “valid”, or “same”. Case insensitive. Defaults to “full”.conjugate (bool) – If True, the complex conjugate of the filter is applied. Defaults to False.
- Output:
y ([…,M], tf.complex or tf.float) – Filtered input. It is tf.float only if both
xand the filter are tf.float. It is tf.complex otherwise. The length M depends on thepadding.
- property aclr
ACLR of the filter
This ACLR corresponds to what one would obtain from using this filter as pulse shaping filter on an i.i.d. sequence of symbols. The in-band is assumed to range from [-0.5, 0.5] in normalized frequency.
- property coefficients
The filter coefficients (after normalization)
- property length
The filter length in samples
- property normalize
True if the filter is normalized to have unit power. False otherwise.
- property sampling_times
Sampling times in multiples of the symbol duration
- show(response='impulse', scale='lin')[source]
Plot the impulse or magnitude response
Plots the impulse response (time domain) or magnitude response (frequency domain) of the filter.
For the computation of the magnitude response, a minimum DFT size of 1024 is assumed which is obtained through zero padding of the filter coefficients in the time domain.
- Input:
response (str, one of [“impulse”, “magnitude”]) – The desired response type. Defaults to “impulse”
scale (str, one of [“lin”, “db”]) – The y-scale of the magnitude response. Can be “lin” (i.e., linear) or “db” (, i.e., Decibel). Defaults to “lin”.
- property trainable
True if the filter coefficients are trainable. False otherwise.
- property window
The window function that is applied to the filter coefficients. None if no window is applied.
Window functions
HannWindow
- class sionna.signal.HannWindow(length, trainable=False, normalize=False, dtype=tf.float32, **kwargs)[source]
Layer for applying a Hann window function of length
lengthto an inputxof the same length.The window function is applied through element-wise multiplication.
The window function is real-valued, i.e., has tf.float as dtype. The dtype of the output is the same as the dtype of the input
xto which the window function is applied. The window function and the input must have the same precision.The Hann window is defined by
\[w_n = \sin^2 \left( \frac{\pi n}{N} \right), 0 \leq n \leq N-1\]where \(N\) is the window length.
- Parameters:
length (int) – Window length (number of samples).
trainable (bool) – If True, the window coefficients are trainable variables. Defaults to False.
normalize (bool) – If True, the window is normalized to have unit average power per coefficient. Defaults to False.
dtype (tf.DType) – The dtype of the filter coefficients. Must be either tf.float32 or tf.float64. Defaults to tf.float32.
- Input:
x ([…, N], tf.complex or tf.float) – The input to which the window function is applied. The window function is applied along the last dimension. The length of the last dimension
Nmust be the same as thelengthof the window function.- Output:
y ([…,N], tf.complex or tf.float) – Output of the windowing operation. The output has the same shape and dtype as the input
x.
- property coefficients
The window coefficients (after normalization)
- property length
Window length in number of samples
- property normalize
True if the window is normalized to have unit average power per coefficient. False otherwise.
- show(samples_per_symbol, domain='time', scale='lin')
Plot the window in time or frequency domain
For the computation of the Fourier transform, a minimum DFT size of 1024 is assumed which is obtained through zero padding of the window coefficients in the time domain.
- Input:
samples_per_symbol (int) – Number of samples per symbol, i.e., the oversampling factor.
domain (str, one of [“time”, “frequency”]) – The desired domain. Defaults to “time”
scale (str, one of [“lin”, “db”]) – The y-scale of the magnitude in the frequency domain. Can be “lin” (i.e., linear) or “db” (, i.e., Decibel). Defaults to “lin”.
- property trainable
True if the window coefficients are trainable. False otherwise.
HammingWindow
- class sionna.signal.HammingWindow(length, trainable=False, normalize=False, dtype=tf.float32, **kwargs)[source]
Layer for applying a Hamming window function of length
lengthto an inputxof the same length.The window function is applied through element-wise multiplication.
The window function is real-valued, i.e., has tf.float as dtype. The dtype of the output is the same as the dtype of the input
xto which the window function is applied. The window function and the input must have the same precision.The Hamming window is defined by
\[w_n = a_0 - (1-a_0) \cos \left( \frac{2 \pi n}{N} \right), 0 \leq n \leq N-1\]where \(N\) is the window length and \(a_0 = \frac{25}{46}\).
- Parameters:
length (int) – Window length (number of samples).
trainable (bool) – If True, the window coefficients are trainable variables. Defaults to False.
normalize (bool) – If True, the window is normalized to have unit average power per coefficient. Defaults to False.
dtype (tf.DType) – The dtype of the filter coefficients. Must be either tf.float32 or tf.float64. Defaults to tf.float32.
- Input:
x ([…, N], tf.complex or tf.float) – The input to which the window function is applied. The window function is applied along the last dimension. The length of the last dimension
Nmust be the same as thelengthof the window function.- Output:
y ([…,N], tf.complex or tf.float) – Output of the windowing operation. The output has the same shape and dtype as the input
x.
- property coefficients
The window coefficients (after normalization)
- property length
Window length in number of samples
- property normalize
True if the window is normalized to have unit average power per coefficient. False otherwise.
- show(samples_per_symbol, domain='time', scale='lin')
Plot the window in time or frequency domain
For the computation of the Fourier transform, a minimum DFT size of 1024 is assumed which is obtained through zero padding of the window coefficients in the time domain.
- Input:
samples_per_symbol (int) – Number of samples per symbol, i.e., the oversampling factor.
domain (str, one of [“time”, “frequency”]) – The desired domain. Defaults to “time”
scale (str, one of [“lin”, “db”]) – The y-scale of the magnitude in the frequency domain. Can be “lin” (i.e., linear) or “db” (, i.e., Decibel). Defaults to “lin”.
- property trainable
True if the window coefficients are trainable. False otherwise.
BlackmanWindow
- class sionna.signal.BlackmanWindow(length, trainable=False, normalize=False, dtype=tf.float32, **kwargs)[source]
Layer for applying a Blackman window function of length
lengthto an inputxof the same length.The window function is applied through element-wise multiplication.
The window function is real-valued, i.e., has tf.float as dtype. The dtype of the output is the same as the dtype of the input
xto which the window function is applied. The window function and the input must have the same precision.The Blackman window is defined by
\[w_n = a_0 - a_1 \cos \left( \frac{2 \pi n}{N} \right) + a_2 \cos \left( \frac{4 \pi n}{N} \right), 0 \leq n \leq N-1\]where \(N\) is the window length, \(a_0 = \frac{7938}{18608}\), \(a_1 = \frac{9240}{18608}\), and \(a_2 = \frac{1430}{18608}\).
- Parameters:
length (int) – Window length (number of samples).
trainable (bool) – If True, the window coefficients are trainable variables. Defaults to False.
normalize (bool) – If True, the window is normalized to have unit average power per coefficient. Defaults to False.
dtype (tf.DType) – The dtype of the filter coefficients. Must be either tf.float32 or tf.float64. Defaults to tf.float32.
- Input:
x ([…, N], tf.complex or tf.float) – The input to which the window function is applied. The window function is applied along the last dimension. The length of the last dimension
Nmust be the same as thelengthof the window function.- Output:
y ([…,N], tf.complex or tf.float) – Output of the windowing operation. The output has the same shape and dtype as the input
x.
- property coefficients
The window coefficients (after normalization)
- property length
Window length in number of samples
- property normalize
True if the window is normalized to have unit average power per coefficient. False otherwise.
- show(samples_per_symbol, domain='time', scale='lin')
Plot the window in time or frequency domain
For the computation of the Fourier transform, a minimum DFT size of 1024 is assumed which is obtained through zero padding of the window coefficients in the time domain.
- Input:
samples_per_symbol (int) – Number of samples per symbol, i.e., the oversampling factor.
domain (str, one of [“time”, “frequency”]) – The desired domain. Defaults to “time”
scale (str, one of [“lin”, “db”]) – The y-scale of the magnitude in the frequency domain. Can be “lin” (i.e., linear) or “db” (, i.e., Decibel). Defaults to “lin”.
- property trainable
True if the window coefficients are trainable. False otherwise.
CustomWindow
- class sionna.signal.CustomWindow(length, coefficients=None, trainable=False, normalize=False, dtype=tf.float32, **kwargs)[source]
Layer for defining and applying a custom window function of length
lengthto an inputxof the same length.The window function is applied through element-wise multiplication.
The window function is real-valued, i.e., has tf.float as dtype. The dtype of the output is the same as the dtype of the input
xto which the window function is applied. The window function and the input must have the same precision.The window coefficients can be set through the
coefficientsparameter. If not provided, random window coefficients are generated by sampling a Gaussian distribution.- Parameters:
length (int) – Window length (number of samples).
coefficients ([N], tf.float) – Optional window coefficients. If set to None, then a random window of length
lengthis generated by sampling a Gaussian distribution. Defaults to None.trainable (bool) – If True, the window coefficients are trainable variables. Defaults to False.
normalize (bool) – If True, the window is normalized to have unit average power per coefficient. Defaults to False.
dtype (tf.DType) – The dtype of the filter coefficients. Must be either tf.float32 or tf.float64. Defaults to tf.float32.
- Input:
x ([…, N], tf.complex or tf.float) – The input to which the window function is applied. The window function is applied along the last dimension. The length of the last dimension
Nmust be the same as thelengthof the window function.- Output:
y ([…,N], tf.complex or tf.float) – Output of the windowing operation. The output has the same shape and dtype as the input
x.
- property coefficients
The window coefficients (after normalization)
- property length
Window length in number of samples
- property normalize
True if the window is normalized to have unit average power per coefficient. False otherwise.
- show(samples_per_symbol, domain='time', scale='lin')
Plot the window in time or frequency domain
For the computation of the Fourier transform, a minimum DFT size of 1024 is assumed which is obtained through zero padding of the window coefficients in the time domain.
- Input:
samples_per_symbol (int) – Number of samples per symbol, i.e., the oversampling factor.
domain (str, one of [“time”, “frequency”]) – The desired domain. Defaults to “time”
scale (str, one of [“lin”, “db”]) – The y-scale of the magnitude in the frequency domain. Can be “lin” (i.e., linear) or “db” (, i.e., Decibel). Defaults to “lin”.
- property trainable
True if the window coefficients are trainable. False otherwise.
Window
- class sionna.signal.Window(length, trainable=False, normalize=False, dtype=tf.float32, **kwargs)[source]
This is an abtract class for defining and applying a window function of length
lengthto an inputxof the same length.The window function is applied through element-wise multiplication.
The window function is real-valued, i.e., has tf.float as dtype. The dtype of the output is the same as the dtype of the input
xto which the window function is applied. The window function and the input must have the same precision.- Parameters:
length (int) – Window length (number of samples).
trainable (bool) – If True, the window coefficients are trainable variables. Defaults to False.
normalize (bool) – If True, the window is normalized to have unit average power per coefficient. Defaults to False.
dtype (tf.DType) – The dtype of the filter coefficients. Must be either tf.float32 or tf.float64. Defaults to tf.float32.
- Input:
x ([…, N], tf.complex or tf.float) – The input to which the window function is applied. The window function is applied along the last dimension. The length of the last dimension
Nmust be the same as thelengthof the window function.- Output:
y ([…,N], tf.complex or tf.float) – Output of the windowing operation. The output has the same shape and dtype as the input
x.
- property coefficients
The window coefficients (after normalization)
- property length
Window length in number of samples
- property normalize
True if the window is normalized to have unit average power per coefficient. False otherwise.
- show(samples_per_symbol, domain='time', scale='lin')[source]
Plot the window in time or frequency domain
For the computation of the Fourier transform, a minimum DFT size of 1024 is assumed which is obtained through zero padding of the window coefficients in the time domain.
- Input:
samples_per_symbol (int) – Number of samples per symbol, i.e., the oversampling factor.
domain (str, one of [“time”, “frequency”]) – The desired domain. Defaults to “time”
scale (str, one of [“lin”, “db”]) – The y-scale of the magnitude in the frequency domain. Can be “lin” (i.e., linear) or “db” (, i.e., Decibel). Defaults to “lin”.
- property trainable
True if the window coefficients are trainable. False otherwise.
Utility Functions
convolve
- sionna.signal.convolve(inp, ker, padding='full', axis=-1)[source]
Filters an input
inpof length N by convolving it with a kernelkerof length K.The length of the kernel
kermust not be greater than the one of the input sequenceinp.The dtype of the output is tf.float only if both
inpandkerare tf.float. It is tf.complex otherwise.inpandkermust have the same precision.Three padding modes are available:
“full” (default): Returns the convolution at each point of overlap between
kerandinp. The length of the output is N + K - 1. Zero-padding of the inputinpis performed to compute the convolution at the border points.“same”: Returns an output of the same length as the input
inp. The convolution is computed such that the coefficients of the inputinpare centered on the coefficient of the kernelkerwith index(K-1)/2for kernels of odd length, andK/2 - 1for kernels of even length. Zero-padding of the input signal is performed to compute the convolution at the border points.“valid”: Returns the convolution only at points where
inpandkercompletely overlap. The length of the output is N - K + 1.
- Input:
inp ([…,N], tf.complex or tf.real) – Input to filter.
ker ([K], tf.complex or tf.real) – Kernel of the convolution.
padding (string) – Padding mode. Must be one of “full”, “valid”, or “same”. Case insensitive. Defaults to “full”.
axis (int) – Axis along which to perform the convolution. Defaults to -1.
- Output:
out ([…,M], tf.complex or tf.float) – Convolution output. It is tf.float only if both
inpandkerare tf.float. It is tf.complex otherwise. The length M of the output depends on thepadding.
fft
- sionna.signal.fft(tensor, axis=-1)[source]
Computes the normalized DFT along a specified axis.
This operation computes the normalized one-dimensional discrete Fourier transform (DFT) along the
axisdimension of atensor. For a vector \(\mathbf{x}\in\mathbb{C}^N\), the DFT \(\mathbf{X}\in\mathbb{C}^N\) is computed as\[X_m = \frac{1}{\sqrt{N}}\sum_{n=0}^{N-1} x_n \exp \left\{ -j2\pi\frac{mn}{N}\right\},\quad m=0,\dots,N-1.\]- Input:
tensor (tf.complex) – Tensor of arbitrary shape.
axis (int) – Indicates the dimension along which the DFT is taken.
- Output:
tf.complex – Tensor of the same dtype and shape as
tensor.
ifft
- sionna.signal.ifft(tensor, axis=-1)[source]
Computes the normalized IDFT along a specified axis.
This operation computes the normalized one-dimensional discrete inverse Fourier transform (IDFT) along the
axisdimension of atensor. For a vector \(\mathbf{X}\in\mathbb{C}^N\), the IDFT \(\mathbf{x}\in\mathbb{C}^N\) is computed as\[x_n = \frac{1}{\sqrt{N}}\sum_{m=0}^{N-1} X_m \exp \left\{ j2\pi\frac{mn}{N}\right\},\quad n=0,\dots,N-1.\]- Input:
tensor (tf.complex) – Tensor of arbitrary shape.
axis (int) – Indicates the dimension along which the IDFT is taken.
- Output:
tf.complex – Tensor of the same dtype and shape as
tensor.
Upsampling
- class sionna.signal.Upsampling(samples_per_symbol, axis=-1, **kwargs)[source]
Upsamples a tensor along a specified axis by inserting zeros between samples.
- Parameters:
samples_per_symbol (int) – The upsampling factor. If
samples_per_symbolis equal to n, then the upsampled axis will be n-times longer.axis (int) – The dimension to be up-sampled. Must not be the first dimension.
- Input:
x ([…,n,…], tf.DType) – The tensor to be upsampled. n is the size of the axis dimension.
- Output:
y ([…,n*samples_per_symbol,…], same dtype as
x) – The upsampled tensor.
Downsampling
- class sionna.signal.Downsampling(samples_per_symbol, offset=0, num_symbols=None, axis=-1, **kwargs)[source]
Downsamples a tensor along a specified axis by retaining one out of
samples_per_symbolelements.- Parameters:
samples_per_symbol (int) – The downsampling factor. If
samples_per_symbolis equal to n, then the downsampled axis will be n-times shorter.offset (int) – Defines the index of the first element to be retained. Defaults to zero.
num_symbols (int) – Defines the total number of symbols to be retained after downsampling. Defaults to None (i.e., the maximum possible number).
axis (int) – The dimension to be downsampled. Must not be the first dimension.
- Input:
x ([…,n,…], tf.DType) – The tensor to be downsampled. n is the size of the axis dimension.
- Output:
y ([…,k,…], same dtype as
x) – The downsampled tensor, wherekis min((n-offset)//samples_per_symbol,num_symbols).
empirical_psd
- sionna.signal.empirical_psd(x, show=True, oversampling=1.0, ylim=(-30, 3))[source]
Computes the empirical power spectral density.
Computes the empirical power spectral density (PSD) of tensor
xalong the last dimension by averaging over all other dimensions. Note that this function simply returns the averaged absolute squared discrete Fourier spectrum ofx.- Input:
x ([…,N], tf.complex) – The signal of which to compute the PSD.
show (bool) – Indicates if a plot of the PSD should be generated. Defaults to True,
oversampling (float) – The oversampling factor. Defaults to 1.
ylim (tuple of floats) – The limits of the y axis. Defaults to [-30, 3]. Only relevant if
showis True.
- Output:
freqs ([N], float) – The normalized frequencies at which the PSD was evaluated.
psd ([N], float) – The PSD.
empirical_aclr
- sionna.signal.empirical_aclr(x, oversampling=1.0, f_min=-0.5, f_max=0.5)[source]
Computes the empirical ACLR.
Computes the empirical adjacent channel leakgae ration (ACLR) of tensor
xbased on its empirical power spectral density (PSD) which is computed along the last dimension by averaging over all other dimensions.It is assumed that the in-band ranges from [
f_min,f_max] in normalized frequency. The ACLR is then defined as\[\text{ACLR} = \frac{P_\text{out}}{P_\text{in}}\]where \(P_\text{in}\) and \(P_\text{out}\) are the in-band and out-of-band power, respectively.
- Input:
x ([…,N], complex) – The signal for which to compute the ACLR.
oversampling (float) – The oversampling factor. Defaults to 1.
f_min (float) – The lower border of the in-band in normalized frequency. Defaults to -0.5.
f_max (float) – The upper border of the in-band in normalized frequency. Defaults to 0.5.
- Output:
aclr (float) – The ACLR in linear scale.