MIMO OFDM Transmissions over the CDL Channel Model
In this notebook, you will learn how to setup a realistic simulation of a MIMO point-to-point link between a mobile user terminal (UT) and a base station (BS). Both, uplink and downlink directions are considered. Here is a schematic diagram of the system model with all required components:
The setup includes:
5G LDPC FEC
QAM modulation
OFDM resource grid with configurabel pilot pattern
Multiple data streams
3GPP 38.901 CDL channel models and antenna patterns
ZF Precoding with perfect channel state information
LS Channel estimation with nearest-neighbor interpolation as well as perfect CSI
LMMSE MIMO equalization
You will learn how to simulate the channel in the time and frequency domains and understand when to use which option.
In particular, you will investigate:
The performance over different CDL models
The impact of imperfect CSI
Channel aging due to mobility
Inter-symbol interference due to insufficient cyclic prefix length
We will first walk through the configuration of all components of the system model, before simulating some simple transmissions in the time and frequency domain. Then, we will build a general Keras model which will allow us to run efficiently simulations with different parameter settings.
This is a notebook demonstrating a fairly advanced use of the Sionna library. It is recommended that you familiarize yourself with the API documentation of the Channel module and understand the difference between time- and frequency-domain modeling. Some of the simulations take some time, especially when you have no GPU available. For this reason, we provide the simulation results within the cells generating the figures. If you want to visualize your own results, just comment the corresponding line.
Table of Contents
GPU Configuration and Imports
[1]:
import os
if os.getenv("CUDA_VISIBLE_DEVICES") is None:
gpu_num = 0 # Use "" to use the CPU
os.environ["CUDA_VISIBLE_DEVICES"] = f"{gpu_num}"
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '3'
# Import Sionna
try:
import sionna
except ImportError as e:
# Install Sionna if package is not already installed
import os
os.system("pip install sionna")
import sionna
# Configure the notebook to use only a single GPU and allocate only as much memory as needed
# For more details, see https://www.tensorflow.org/guide/gpu
import tensorflow as tf
gpus = tf.config.list_physical_devices('GPU')
if gpus:
try:
tf.config.experimental.set_memory_growth(gpus[0], True)
except RuntimeError as e:
print(e)
tf.get_logger().setLevel('ERROR')
# Set random seed for reproducibility
sionna.config.seed = 42
[2]:
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pickle
import time
from sionna.mimo import StreamManagement
from sionna.ofdm import ResourceGrid, ResourceGridMapper, LSChannelEstimator, LMMSEEqualizer
from sionna.ofdm import OFDMModulator, OFDMDemodulator, ZFPrecoder, RemoveNulledSubcarriers
from sionna.channel.tr38901 import AntennaArray, CDL, Antenna
from sionna.channel import subcarrier_frequencies, cir_to_ofdm_channel, cir_to_time_channel, time_lag_discrete_time_channel
from sionna.channel import ApplyOFDMChannel, ApplyTimeChannel, OFDMChannel, TimeChannel
from sionna.fec.ldpc.encoding import LDPC5GEncoder
from sionna.fec.ldpc.decoding import LDPC5GDecoder
from sionna.mapping import Mapper, Demapper
from sionna.utils import BinarySource, ebnodb2no, sim_ber
from sionna.utils.metrics import compute_ber
System Setup
We will now configure all components of the system model step-by-step.
Stream Management
For any type of MIMO simulations, it is useful to setup a StreamManagement object. It determines which transmitters and receivers communicate data streams with each other. In our scenario, we will configure a single UT and BS with multiple antennas each. Whether the UT or BS is considered as a transmitter depends on the direction, which can be either uplink or downlink. The
StreamManagement has many properties that are used by other components, such as precoding and equalization.
We will configure the system here such that the number of streams per transmitter (in both uplink and donwlink) is equal to the number of UT antennas.
[3]:
# Define the number of UT and BS antennas.
# For the CDL model, that will be used in this notebook, only
# a single UT and BS are supported.
num_ut = 1
num_bs = 1
num_ut_ant = 4
num_bs_ant = 8
# The number of transmitted streams is equal to the number of UT antennas
# in both uplink and downlink
num_streams_per_tx = num_ut_ant
# Create an RX-TX association matrix
# rx_tx_association[i,j]=1 means that receiver i gets at least one stream
# from transmitter j. Depending on the transmission direction (uplink or downlink),
# the role of UT and BS can change. However, as we have only a single
# transmitter and receiver, this does not matter:
rx_tx_association = np.array([[1]])
# Instantiate a StreamManagement object
# This determines which data streams are determined for which receiver.
# In this simple setup, this is fairly easy. However, it can get more involved
# for simulations with many transmitters and receivers.
sm = StreamManagement(rx_tx_association, num_streams_per_tx)
OFDM Resource Grid & Pilot Pattern
Next, we configure an OFDM ResourceGrid spanning multiple OFDM symbols. The resource grid contains data symbols and pilots and is equivalent to a slot in 4G/5G terminology. Although it is not relevant for our simulation, we null the DC subcarrier and a few guard carriers to the left and right of the spectrum. Also a cyclic prefix is added.
During the creation of the ResourceGrid, a PilotPattern is automatically generated. We could have alternatively created a PilotPattern first and then provided it as initialization parameter.
[4]:
rg = ResourceGrid(num_ofdm_symbols=14,
fft_size=76,
subcarrier_spacing=15e3,
num_tx=1,
num_streams_per_tx=num_streams_per_tx,
cyclic_prefix_length=6,
num_guard_carriers=[5,6],
dc_null=True,
pilot_pattern="kronecker",
pilot_ofdm_symbol_indices=[2,11])
rg.show();
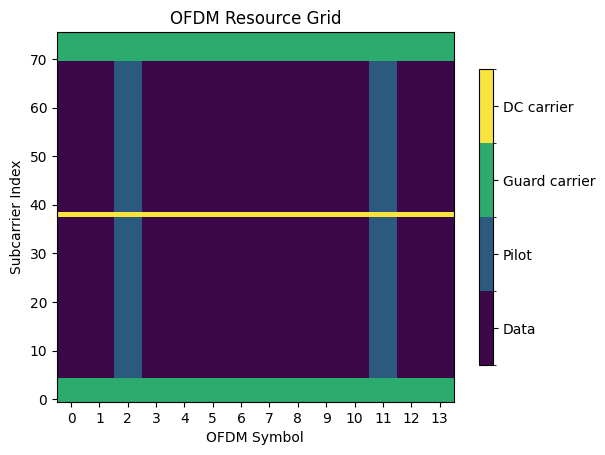
As can be seen in the figure above, the resource grid spans 76 subcarriers over 14 OFDM symbols. A DC guard carrier as well as some guard carriers to the left and right of the spectrum are nulled. The third and twelfth OFDM symbol are dedicated to pilot transmissions.
Let us now have a look at the pilot pattern used by the transmitter.
[5]:
rg.pilot_pattern.show();
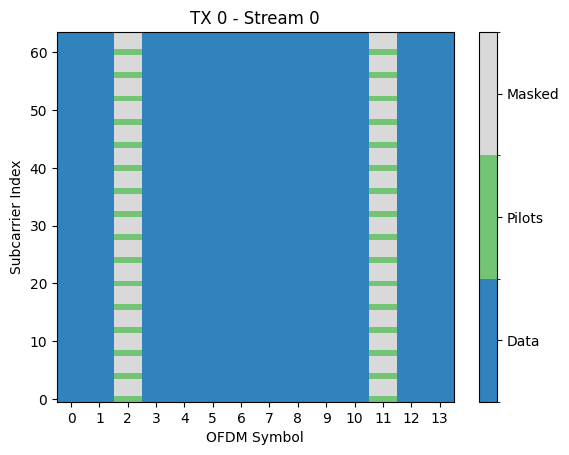
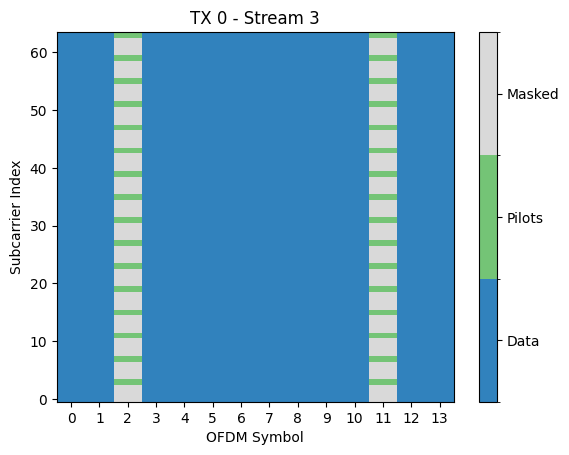
The pilot patterns are defined over the resource grid of effective subcarriers from which the nulled DC and guard carriers have been removed. This leaves us in our case with 76 - 1 (DC) - 5 (left guards) - 6 (right guards) = 64 effective subcarriers.
While the resource grid only knows which resource elements are reserved for pilots, it is the pilot pattern that defines what is actually transmitted on them. In our scenario, we have four transmit streams and configured the KroneckerPilotPattern. All streams use orthogonal pilot sequences, i.e., one pilot on every fourth subcarrier. You have full freedom to configure your own PilotPattern.
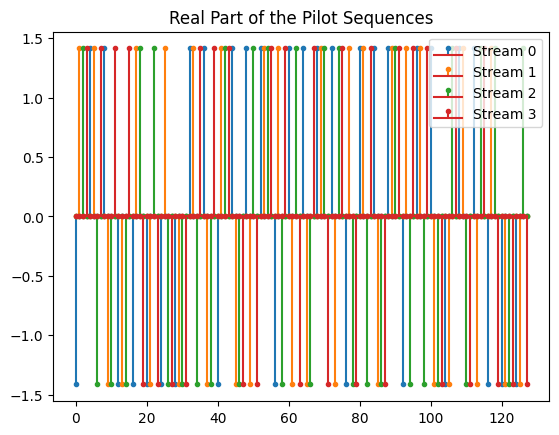
Let us now have a look at the actual pilot sequences for all streams which consists of random QPSK symbols. By default, the pilot sequences are normalized, such that the average power per pilot symbol is equal to one. As only every fourth pilot symbol in the sequence is used, their amplitude is scaled by a factor of two.
[6]:
plt.figure()
plt.title("Real Part of the Pilot Sequences")
for i in range(num_streams_per_tx):
plt.stem(np.real(rg.pilot_pattern.pilots[0, i]),
markerfmt="C{}.".format(i), linefmt="C{}-".format(i),
label="Stream {}".format(i))
plt.legend()
print("Average energy per pilot symbol: {:1.2f}".format(np.mean(np.abs(rg.pilot_pattern.pilots[0,0])**2)))
Average energy per pilot symbol: 1.00
Antenna Arrays
Next, we need to configure the antenna arrays used by the UT and BS. This can be ignored for simple channel models, such as AWGN, flat-fading, RayleighBlockFading, or TDL which do not account for antenna array geometries and antenna radiation patterns. However, other models, such as CDL, UMi, UMa, and RMa from the 3GPP 38.901 specification, require it.
We will assume here that UT and BS antenna arrays are composed of dual cross-polarized antenna elements with an antenna pattern defined in the 3GPP 38.901 specification. By default, the antenna elements are spaced half of a wavelength apart in both vertical and horizontal directions. You can define your own antenna geometries an radiation patterns if needed.
An AntennaArray is always defined in the y-z plane. It’s final orientation will be determined by the orientation of the UT or BS. This parameter can be configured in the ChannelModel that we will create later.
[7]:
carrier_frequency = 2.6e9 # Carrier frequency in Hz.
# This is needed here to define the antenna element spacing.
ut_array = AntennaArray(num_rows=1,
num_cols=int(num_ut_ant/2),
polarization="dual",
polarization_type="cross",
antenna_pattern="38.901",
carrier_frequency=carrier_frequency)
ut_array.show()
bs_array = AntennaArray(num_rows=1,
num_cols=int(num_bs_ant/2),
polarization="dual",
polarization_type="cross",
antenna_pattern="38.901",
carrier_frequency=carrier_frequency)
bs_array.show()
We can also visualize the radiation pattern of an individual antenna element:
[8]:
ut_array.show_element_radiation_pattern()
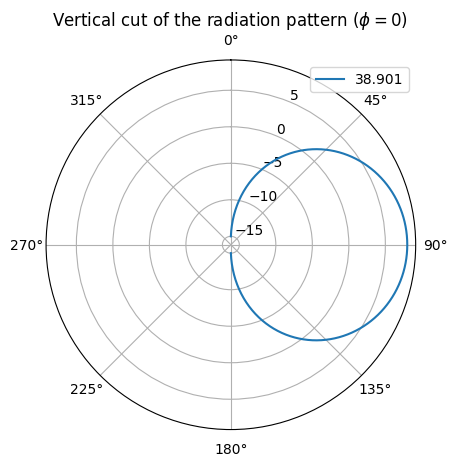
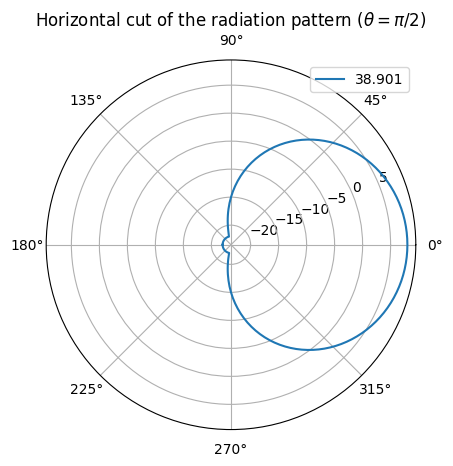
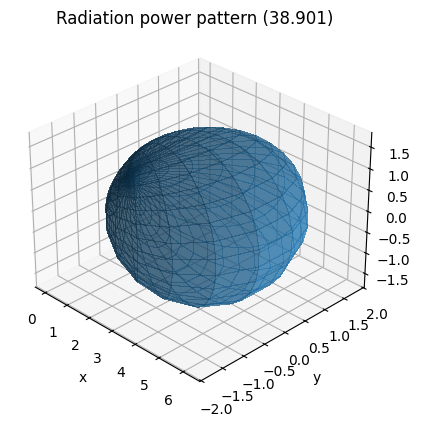
CDL Channel Model
Now, we will create an instance of the CDL channel model.
[9]:
delay_spread = 300e-9 # Nominal delay spread in [s]. Please see the CDL documentation
# about how to choose this value.
direction = "uplink" # The `direction` determines if the UT or BS is transmitting.
# In the `uplink`, the UT is transmitting.
cdl_model = "B" # Suitable values are ["A", "B", "C", "D", "E"]
speed = 10 # UT speed [m/s]. BSs are always assumed to be fixed.
# The direction of travel will chosen randomly within the x-y plane.
# Configure a channel impulse reponse (CIR) generator for the CDL model.
# cdl() will generate CIRs that can be converted to discrete time or discrete frequency.
cdl = CDL(cdl_model, delay_spread, carrier_frequency, ut_array, bs_array, direction, min_speed=speed)
CIR Sampling Process
The instance cdl of the CDL ChannelModel can be used to generate batches of random realizations of continuous-time channel impulse responses, consisting of complex gains a and delays tau for each path. To account for time-varying channels, a channel impulse responses is sampled at the sampling_frequency for
num_time_samples samples. For more details on this, please have a look at the API documentation of the channel models.
In order to model the channel in the frequency domain, we need num_ofdm_symbols samples that are taken once per ofdm_symbol_duration, which corresponds to the length of an OFDM symbol plus the cyclic prefix.
[10]:
a, tau = cdl(batch_size=32, num_time_steps=rg.num_ofdm_symbols, sampling_frequency=1/rg.ofdm_symbol_duration)
a have shape[batch size, num_rx, num_rx_ant, num_tx, num_tx_ant, num_paths, num_time_steps]tau have shape[batch_size, num_rx, num_tx, num_paths].[11]:
print("Shape of the path gains: ", a.shape)
print("Shape of the delays:", tau.shape)
Shape of the path gains: (32, 1, 8, 1, 4, 23, 14)
Shape of the delays: (32, 1, 1, 23)
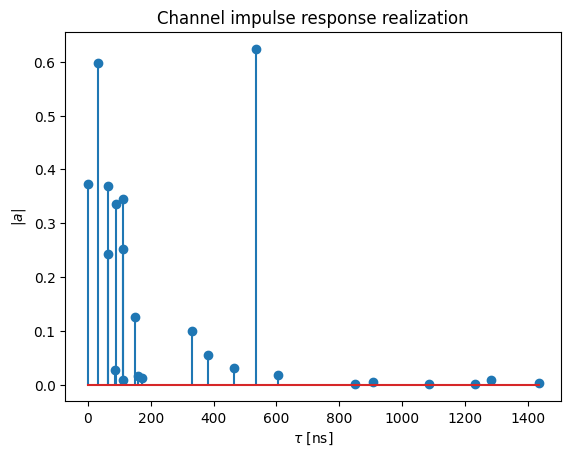
The delays are assumed to be static within the time-window of interest. Only the complex path gains change over time. The following two figures depict the channel impulse response at a particular time instant and the time-evolution of the gain of one path, respectively.
[12]:
plt.figure()
plt.title("Channel impulse response realization")
plt.stem(tau[0,0,0,:]/1e-9, np.abs(a)[0,0,0,0,0,:,0])
plt.xlabel(r"$\tau$ [ns]")
plt.ylabel(r"$|a|$")
plt.figure()
plt.title("Time evolution of path gain")
plt.plot(np.arange(rg.num_ofdm_symbols)*rg.ofdm_symbol_duration/1e-6, np.real(a)[0,0,0,0,0,0,:])
plt.plot(np.arange(rg.num_ofdm_symbols)*rg.ofdm_symbol_duration/1e-6, np.imag(a)[0,0,0,0,0,0,:])
plt.legend(["Real part", "Imaginary part"])
plt.xlabel(r"$t$ [us]")
plt.ylabel(r"$a$");
Generate the Channel Frequency Response
If we want to use the continuous-time channel impulse response to simulate OFDM transmissions under ideal conditions, i.e., no inter-symbol interference, inter-carrier interference, etc., we need to convert it to the frequency domain.
This can be done with the function cir_to_ofdm_channel that computes the Fourier transform of the continuous-time channel impulse response at a set of frequencies, corresponding to the different subcarriers. The frequencies can be obtained with the help of the convenience function subcarrier_frequencies.
[13]:
frequencies = subcarrier_frequencies(rg.fft_size, rg.subcarrier_spacing)
h_freq = cir_to_ofdm_channel(frequencies, a, tau, normalize=True)
Let us have a look at the channel frequency response at a given time instant:
[14]:
plt.figure()
plt.title("Channel frequency response")
plt.plot(np.real(h_freq[0,0,0,0,0,0,:]))
plt.plot(np.imag(h_freq[0,0,0,0,0,0,:]))
plt.xlabel("OFDM Symbol Index")
plt.ylabel(r"$h$")
plt.legend(["Real part", "Imaginary part"]);
We can apply the channel frequency response to a given input with the ApplyOFDMChannel layer. This layer can also add additive white Gaussian noise (AWGN) to the channel output.
[15]:
# Function that will apply the channel frequency response to an input signal
channel_freq = ApplyOFDMChannel(add_awgn=True)
Generate the Discrete-Time Channel Impulse Response
In the same way as we have created the frequency channel impulse response from the continuous-time response, we can use the latter to compute a discrete-time impulse response. This can then be used to model the channel in the time-domain through discrete convolution with an input signal. Time-domain channel modeling is necessary whenever we want to deviate from the perfect OFDM scenario, e.g., OFDM without cyclic prefix, inter-subcarrier interference due to carrier-frequency offsets, phase noise, or very high Doppler spread scenarios, as well as other single or multicarrier waveforms (OTFS, FBMC, UFMC, etc).
A discrete-time impulse response can be obtained with the help of the function cir_to_time_channel that requires a bandwidth parameter. This function first applies a perfect low-pass filter of the provided bandwith to the continuous-time channel impulse response and then samples the filtered response at the Nyquist rate. The resulting discrete-time impulse response is then truncated to finite length, depending on
the delay spread. l_min and l_max denote truncation boundaries and the resulting channel has l_tot=l_max-l_min+1 filter taps. A detailed mathematical description of this process is provided in the API documentation of the channel models. You can freely chose both parameters if you do not want to rely on the default values.
In order to model the channel in the domain, the continuous-time channel impulse response must be sampled at the Nyquist rate. We also need now num_ofdm_symbols x (fft_size + cyclic_prefix_length) + l_tot-1 samples in contrast to num_ofdm_symbols samples for modeling in the frequency domain. This implies that the memory requirements of time-domain channel modeling is significantly higher. We therefore recommend to only use this feature if it is really necessary. Simulations with many
transmitters, receivers, and/or large antenna arrays become otherwise quickly prohibitively complex.
[16]:
# The following values for truncation are recommended.
# Please feel free to tailor them to you needs.
l_min, l_max = time_lag_discrete_time_channel(rg.bandwidth)
l_tot = l_max-l_min+1
a, tau = cdl(batch_size=2, num_time_steps=rg.num_time_samples+l_tot-1, sampling_frequency=rg.bandwidth)
[17]:
h_time = cir_to_time_channel(rg.bandwidth, a, tau, l_min=l_min, l_max=l_max, normalize=True)
[18]:
plt.figure()
plt.title("Discrete-time channel impulse response")
plt.stem(np.abs(h_time[0,0,0,0,0,0]))
plt.xlabel(r"Time step $\ell$")
plt.ylabel(r"$|\bar{h}|$");
We can apply the discrete-time impulse response to a given input with the ApplyTimeChannel layer. This layer can also add additive white Gaussian noise (AWGN) to the channel output.
[19]:
# Function that will apply the discrete-time channel impulse response to an input signal
channel_time = ApplyTimeChannel(rg.num_time_samples, l_tot=l_tot, add_awgn=True)
Other Physical Layer Components
Finally, we create instances of all other physical layer components we need. Most of these layers are self-explanatory. For more information, please have a look at the API documentation.
[20]:
num_bits_per_symbol = 2 # QPSK modulation
coderate = 0.5 # Code rate
n = int(rg.num_data_symbols*num_bits_per_symbol) # Number of coded bits
k = int(n*coderate) # Number of information bits
# The binary source will create batches of information bits
binary_source = BinarySource()
# The encoder maps information bits to coded bits
encoder = LDPC5GEncoder(k, n)
# The mapper maps blocks of information bits to constellation symbols
mapper = Mapper("qam", num_bits_per_symbol)
# The resource grid mapper maps symbols onto an OFDM resource grid
rg_mapper = ResourceGridMapper(rg)
# The zero forcing precoder precodes the transmit stream towards the intended antennas
zf_precoder = ZFPrecoder(rg, sm, return_effective_channel=True)
# OFDM modulator and demodulator
modulator = OFDMModulator(rg.cyclic_prefix_length)
demodulator = OFDMDemodulator(rg.fft_size, l_min, rg.cyclic_prefix_length)
# This function removes nulled subcarriers from any tensor having the shape of a resource grid
remove_nulled_scs = RemoveNulledSubcarriers(rg)
# The LS channel estimator will provide channel estimates and error variances
ls_est = LSChannelEstimator(rg, interpolation_type="nn")
# The LMMSE equalizer will provide soft symbols together with noise variance estimates
lmmse_equ = LMMSEEqualizer(rg, sm)
# The demapper produces LLR for all coded bits
demapper = Demapper("app", "qam", num_bits_per_symbol)
# The decoder provides hard-decisions on the information bits
decoder = LDPC5GDecoder(encoder, hard_out=True)
Simulations
Uplink Transmission in the Frequency Domain
Now, we will simulate our first uplink transmission! Inspect the code to understand how perfect CSI at the receiver can be simulated.
[21]:
batch_size = 32 # Depending on the memory of your GPU (or system when a CPU is used),
# you can in(de)crease the batch size. The larger the batch size, the
# more memory is required. However, simulations will also run much faster.
ebno_db = 40
perfect_csi = False # Change to switch between perfect and imperfect CSI
# Compute the noise power for a given Eb/No value.
# This takes not only the coderate but also the overheads related pilot
# transmissions and nulled carriers
no = ebnodb2no(ebno_db, num_bits_per_symbol, coderate, rg)
b = binary_source([batch_size, 1, rg.num_streams_per_tx, encoder.k])
c = encoder(b)
x = mapper(c)
x_rg = rg_mapper(x)
# As explained above, we generate random batches of CIR, transform them
# in the frequency domain and apply them to the resource grid in the
# frequency domain.
cir = cdl(batch_size, rg.num_ofdm_symbols, 1/rg.ofdm_symbol_duration)
h_freq = cir_to_ofdm_channel(frequencies, *cir, normalize=True)
y = channel_freq([x_rg, h_freq, no])
if perfect_csi:
# For perfect CSI, the receiver gets the channel frequency response as input
# However, the channel estimator only computes estimates on the non-nulled
# subcarriers. Therefore, we need to remove them here from `h_freq`.
# This step can be skipped if no subcarriers are nulled.
h_hat, err_var = remove_nulled_scs(h_freq), 0.
else:
h_hat, err_var = ls_est ([y, no])
x_hat, no_eff = lmmse_equ([y, h_hat, err_var, no])
llr = demapper([x_hat, no_eff])
b_hat = decoder(llr)
ber = compute_ber(b, b_hat)
print("BER: {}".format(ber))
BER: 0.0
An alternative approach to simulations in the frequency domain is to use the convenience function OFDMChannel that jointly generates and applies the channel frequency response. Using this function, we could have used the following code:
[22]:
ofdm_channel = OFDMChannel(cdl, rg, add_awgn=True, normalize_channel=True, return_channel=True)
y, h_freq = ofdm_channel([x_rg, no])
Uplink Transmission in the Time Domain
In the previous example, OFDM modulation/demodulation were not needed as the entire system was simulated in the frequency domain. However, this modeling approach is not able to capture many realistic effects.
With the following modifications, the system can be modeled in the time domain.
Have a careful look at how perfect CSI of the channel frequency response is simulated here.
[23]:
batch_size = 4 # We pick a small batch_size as executing this code in Eager mode could consume a lot of memory
ebno_db = 30
perfect_csi = True
no = ebnodb2no(ebno_db, num_bits_per_symbol, coderate, rg)
b = binary_source([batch_size, 1, rg.num_streams_per_tx, encoder.k])
c = encoder(b)
x = mapper(c)
x_rg = rg_mapper(x)
# The CIR needs to be sampled every 1/bandwith [s].
# In contrast to frequency-domain modeling, this implies
# that the channel can change over the duration of a single
# OFDM symbol. We now also need to simulate more
# time steps.
cir = cdl(batch_size, rg.num_time_samples+l_tot-1, rg.bandwidth)
# OFDM modulation with cyclic prefix insertion
x_time = modulator(x_rg)
# Compute the discrete-time channel impulse reponse
h_time = cir_to_time_channel(rg.bandwidth, *cir, l_min, l_max, normalize=True)
# Compute the channel output
# This computes the full convolution between the time-varying
# discrete-time channel impulse reponse and the discrete-time
# transmit signal. With this technique, the effects of an
# insufficiently long cyclic prefix will become visible. This
# is in contrast to frequency-domain modeling which imposes
# no inter-symbol interfernce.
y_time = channel_time([x_time, h_time, no])
# OFDM demodulation and cyclic prefix removal
y = demodulator(y_time)
if perfect_csi:
a, tau = cir
# We need to sub-sample the channel impulse reponse to compute perfect CSI
# for the receiver as it only needs one channel realization per OFDM symbol
a_freq = a[...,rg.cyclic_prefix_length:-1:(rg.fft_size+rg.cyclic_prefix_length)]
a_freq = a_freq[...,:rg.num_ofdm_symbols]
# Compute the channel frequency response
h_freq = cir_to_ofdm_channel(frequencies, a_freq, tau, normalize=True)
h_hat, err_var = remove_nulled_scs(h_freq), 0.
else:
h_hat, err_var = ls_est ([y, no])
x_hat, no_eff = lmmse_equ([y, h_hat, err_var, no])
llr = demapper([x_hat, no_eff])
b_hat = decoder(llr)
ber = compute_ber(b, b_hat)
print("BER: {}".format(ber))
BER: 0.0
An alternative approach to simulations in the time domain is to use the convenience function TimeChannel that jointly generates and applies the discrete-time channel impulse response. Using this function, we could have used the following code:
[24]:
time_channel = TimeChannel(cdl, rg.bandwidth, rg.num_time_samples,
l_min=l_min, l_max=l_max, normalize_channel=True,
add_awgn=True, return_channel=True)
y_time, h_time = time_channel([x_time, no])
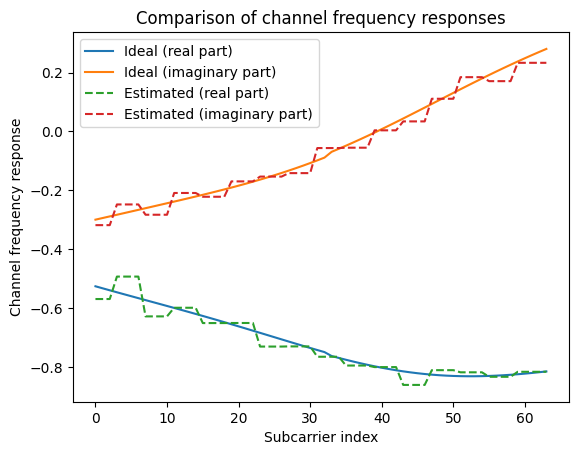
Next, we will compare the perfect CSI that we computed above using the ideal channel frequency response and the estimated channel response that we obtain from pilots with nearest-neighbor interpolation based on simulated transmissions in the time domain.
[25]:
# In the example above, we assumed perfect CSI, i.e.,
# h_hat correpsond to the exact ideal channel frequency response.
h_perf = h_hat[0,0,0,0,0,0]
# We now compute the LS channel estimate from the pilots.
h_est, _ = ls_est ([y, no])
h_est = h_est[0,0,0,0,0,0]
[26]:
plt.figure()
plt.plot(np.real(h_perf))
plt.plot(np.imag(h_perf))
plt.plot(np.real(h_est), "--")
plt.plot(np.imag(h_est), "--")
plt.xlabel("Subcarrier index")
plt.ylabel("Channel frequency response")
plt.legend(["Ideal (real part)", "Ideal (imaginary part)", "Estimated (real part)", "Estimated (imaginary part)"]);
plt.title("Comparison of channel frequency responses");
Downlink Transmission in the Frequency Domain
We will now simulate a simple downlink transmission in the frequency domain. In contrast to the uplink, the transmitter is now assumed to precode independent data streams to each antenna of the receiver based on perfect CSI.
The receiver can either estimate the channel or get access to the effective channel after precoding.
The first thing to do, is to change the direction within the CDL model. This makes the BS the transmitter and the UT the receiver.
[27]:
direction = "downlink"
cdl = CDL(cdl_model, delay_spread, carrier_frequency, ut_array, bs_array, direction, min_speed=speed)
The following code shows the other necessary modifications:
[28]:
perfect_csi = True # Change to switch between perfect and imperfect CSI
no = ebnodb2no(ebno_db, num_bits_per_symbol, coderate, rg)
b = binary_source([batch_size, 1, rg.num_streams_per_tx, encoder.k])
c = encoder(b)
x = mapper(c)
x_rg = rg_mapper(x)
cir = cdl(batch_size, rg.num_ofdm_symbols, 1/rg.ofdm_symbol_duration)
h_freq = cir_to_ofdm_channel(frequencies, *cir, normalize=True)
# Precode the transmit signal in the frequency domain
# It is here assumed that the transmitter has perfect knowledge of the channel
# One could here reduce this to perfect knowledge of the channel for the first
# OFDM symbol, or a noisy version of it to take outdated transmit CSI into account.
# `g` is the post-beamforming or `effective channel` that can be
# used to simulate perfect CSI at the receiver.
x_rg, g = zf_precoder([x_rg, h_freq])
y = channel_freq([x_rg, h_freq, no])
if perfect_csi:
# The receiver gets here the effective channel after precoding as CSI
h_hat, err_var = g, 0.
else:
h_hat, err_var = ls_est ([y, no])
x_hat, no_eff = lmmse_equ([y, h_hat, err_var, no])
llr = demapper([x_hat, no_eff])
b_hat = decoder(llr)
ber = compute_ber(b, b_hat)
print("BER: {}".format(ber))
BER: 0.0
We do not explain here on purpose how to model the downlink transmission in the time domain as it is a good exercise for the reader to do it her/himself. The key steps are:
Sample the channel impulse response at the Nyquist rate.
Downsample it to the OFDM symbol (+ cyclic prefix) rate (look at the uplink example).
Convert the downsampled CIR to the frequency domain.
Give this CSI to the transmitter for precoding.
Convert the CIR to discrete-time to compute the channel output in the time domain.
Understand the Difference Between the CDL Models
Before we proceed with more advanced simulations, it is important to understand the differences between the different CDL models. The models “A”, “B”, and “C” are non-line-of-sight (NLOS) models, while “D” and “E” are LOS. In the following code snippet, we compute the empirical cummulative distribution function (CDF) of the condition number of the channel frequency response matrix between all receiver and transmit antennas.
[29]:
def fun(cdl_model):
"""Generates a histogram of the channel condition numbers"""
# Setup a CIR generator
cdl = CDL(cdl_model, delay_spread, carrier_frequency,
ut_array, bs_array, "uplink", min_speed=0)
# Generate random CIR realizations
# As we nned only a single sample in time, the sampling_frequency
# does not matter.
cir = cdl(2000, 1, 1)
# Compute the frequency response
h = cir_to_ofdm_channel(frequencies, *cir, normalize=True)
# Reshape to [batch_size, fft_size, num_rx_ant, num_tx_ant]
h = tf.squeeze(h)
h = tf.transpose(h, [0,3,1,2])
# Compute condition number
c = np.reshape(np.linalg.cond(h), [-1])
# Compute normalized histogram
hist, bins = np.histogram(c, 150, (1, 150))
hist = hist/np.sum(hist)
return bins[:-1], hist
plt.figure()
for cdl_model in ["A", "B", "C", "D", "E"]:
bins, hist = fun(cdl_model)
plt.plot(bins, np.cumsum(hist))
plt.xlim([0,150])
plt.legend(["CDL-A", "CDL-B", "CDL-C", "CDL-D", "CDL-E"]);
plt.xlabel("Channel Condition Number")
plt.ylabel("CDF")
plt.title("CDF of the condition number of 8x4 MIMO channels");
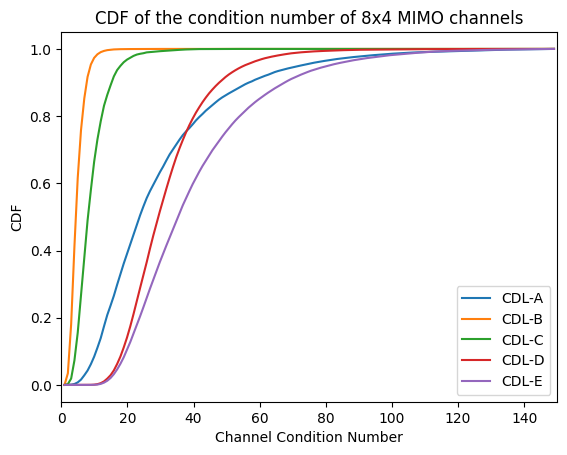
From the figure above, you can observe that the CDL-B and CDL-C models are substantially better conditioned than the other models. This makes them more suitable for MIMO transmissions as we will observe in the next section.
Create an End-to-End Keras Model
For longer simulations, it is often convenient to pack all code into a single Keras model that outputs batches of transmitted and received information bits at a given Eb/No point. The following code defines a very general model that can simulate uplink and downlink transmissions with time or frequency domain modeling over the different CDL models. It allows to configure perfect or imperfect CSI, UT speed, cyclic prefix length, and the number of OFDM symbols for pilot transmissions.
[30]:
class Model(tf.keras.Model):
"""This Keras model simulates OFDM MIMO transmissions over the CDL model.
Simulates point-to-point transmissions between a UT and a BS.
Uplink and downlink transmissions can be realized with either perfect CSI
or channel estimation. ZF Precoding for downlink transmissions is assumed.
The receiver (in both uplink and downlink) applies LS channel estimation
and LMMSE MIMO equalization. A 5G LDPC code as well as QAM modulation are
used.
Parameters
----------
domain : One of ["time", "freq"], str
Determines if the channel is modeled in the time or frequency domain.
Time-domain simulations are generally slower and consume more memory.
They allow modeling of inter-symbol interference and channel changes
during the duration of an OFDM symbol.
direction : One of ["uplink", "downlink"], str
For "uplink", the UT transmits. For "downlink" the BS transmits.
cdl_model : One of ["A", "B", "C", "D", "E"], str
The CDL model to use. Note that "D" and "E" are LOS models that are
not well suited for the transmissions of multiple streams.
delay_spread : float
The nominal delay spread [s].
perfect_csi : bool
Indicates if perfect CSI at the receiver should be assumed. For downlink
transmissions, the transmitter is always assumed to have perfect CSI.
speed : float
The UT speed [m/s].
cyclic_prefix_length : int
The length of the cyclic prefix in number of samples.
pilot_ofdm_symbol_indices : list, int
List of integers defining the OFDM symbol indices that are reserved
for pilots.
subcarrier_spacing : float
The subcarrier spacing [Hz]. Defaults to 15e3.
Input
-----
batch_size : int
The batch size, i.e., the number of independent Mote Carlo simulations
to be performed at once. The larger this number, the larger the memory
requiremens.
ebno_db : float
The Eb/No [dB]. This value is converted to an equivalent noise power
by taking the modulation order, coderate, pilot and OFDM-related
overheads into account.
Output
------
b : [batch_size, 1, num_streams, k], tf.float32
The tensor of transmitted information bits for each stream.
b_hat : [batch_size, 1, num_streams, k], tf.float32
The tensor of received information bits for each stream.
"""
def __init__(self,
domain,
direction,
cdl_model,
delay_spread,
perfect_csi,
speed,
cyclic_prefix_length,
pilot_ofdm_symbol_indices,
subcarrier_spacing = 15e3
):
super().__init__()
# Provided parameters
self._domain = domain
self._direction = direction
self._cdl_model = cdl_model
self._delay_spread = delay_spread
self._perfect_csi = perfect_csi
self._speed = speed
self._cyclic_prefix_length = cyclic_prefix_length
self._pilot_ofdm_symbol_indices = pilot_ofdm_symbol_indices
# System parameters
self._carrier_frequency = 2.6e9
self._subcarrier_spacing = subcarrier_spacing
self._fft_size = 72
self._num_ofdm_symbols = 14
self._num_ut_ant = 4 # Must be a multiple of two as dual-polarized antennas are used
self._num_bs_ant = 8 # Must be a multiple of two as dual-polarized antennas are used
self._num_streams_per_tx = self._num_ut_ant
self._dc_null = True
self._num_guard_carriers = [5, 6]
self._pilot_pattern = "kronecker"
self._pilot_ofdm_symbol_indices = pilot_ofdm_symbol_indices
self._num_bits_per_symbol = 2
self._coderate = 0.5
# Required system components
self._sm = StreamManagement(np.array([[1]]), self._num_streams_per_tx)
self._rg = ResourceGrid(num_ofdm_symbols=self._num_ofdm_symbols,
fft_size=self._fft_size,
subcarrier_spacing = self._subcarrier_spacing,
num_tx=1,
num_streams_per_tx=self._num_streams_per_tx,
cyclic_prefix_length=self._cyclic_prefix_length,
num_guard_carriers=self._num_guard_carriers,
dc_null=self._dc_null,
pilot_pattern=self._pilot_pattern,
pilot_ofdm_symbol_indices=self._pilot_ofdm_symbol_indices)
self._n = int(self._rg.num_data_symbols * self._num_bits_per_symbol)
self._k = int(self._n * self._coderate)
self._ut_array = AntennaArray(num_rows=1,
num_cols=int(self._num_ut_ant/2),
polarization="dual",
polarization_type="cross",
antenna_pattern="38.901",
carrier_frequency=self._carrier_frequency)
self._bs_array = AntennaArray(num_rows=1,
num_cols=int(self._num_bs_ant/2),
polarization="dual",
polarization_type="cross",
antenna_pattern="38.901",
carrier_frequency=self._carrier_frequency)
self._cdl = CDL(model=self._cdl_model,
delay_spread=self._delay_spread,
carrier_frequency=self._carrier_frequency,
ut_array=self._ut_array,
bs_array=self._bs_array,
direction=self._direction,
min_speed=self._speed)
self._frequencies = subcarrier_frequencies(self._rg.fft_size, self._rg.subcarrier_spacing)
if self._domain == "freq":
self._channel_freq = ApplyOFDMChannel(add_awgn=True)
elif self._domain == "time":
self._l_min, self._l_max = time_lag_discrete_time_channel(self._rg.bandwidth)
self._l_tot = self._l_max - self._l_min + 1
self._channel_time = ApplyTimeChannel(self._rg.num_time_samples,
l_tot=self._l_tot,
add_awgn=True)
self._modulator = OFDMModulator(self._cyclic_prefix_length)
self._demodulator = OFDMDemodulator(self._fft_size, self._l_min, self._cyclic_prefix_length)
self._binary_source = BinarySource()
self._encoder = LDPC5GEncoder(self._k, self._n)
self._mapper = Mapper("qam", self._num_bits_per_symbol)
self._rg_mapper = ResourceGridMapper(self._rg)
if self._direction == "downlink":
self._zf_precoder = ZFPrecoder(self._rg, self._sm, return_effective_channel=True)
self._ls_est = LSChannelEstimator(self._rg, interpolation_type="nn")
self._lmmse_equ = LMMSEEqualizer(self._rg, self._sm)
self._demapper = Demapper("app", "qam", self._num_bits_per_symbol)
self._decoder = LDPC5GDecoder(self._encoder, hard_out=True)
self._remove_nulled_scs = RemoveNulledSubcarriers(self._rg)
@tf.function # Run in graph mode. See the following guide: https://www.tensorflow.org/guide/function
def call(self, batch_size, ebno_db):
no = ebnodb2no(ebno_db, self._num_bits_per_symbol, self._coderate, self._rg)
b = self._binary_source([batch_size, 1, self._num_streams_per_tx, self._k])
c = self._encoder(b)
x = self._mapper(c)
x_rg = self._rg_mapper(x)
if self._domain == "time":
# Time-domain simulations
a, tau = self._cdl(batch_size, self._rg.num_time_samples+self._l_tot-1, self._rg.bandwidth)
h_time = cir_to_time_channel(self._rg.bandwidth, a, tau,
l_min=self._l_min, l_max=self._l_max, normalize=True)
# As precoding is done in the frequency domain, we need to downsample
# the path gains `a` to the OFDM symbol rate prior to converting the CIR
# to the channel frequency response.
a_freq = a[...,self._rg.cyclic_prefix_length:-1:(self._rg.fft_size+self._rg.cyclic_prefix_length)]
a_freq = a_freq[...,:self._rg.num_ofdm_symbols]
h_freq = cir_to_ofdm_channel(self._frequencies, a_freq, tau, normalize=True)
if self._direction == "downlink":
x_rg, g = self._zf_precoder([x_rg, h_freq])
x_time = self._modulator(x_rg)
y_time = self._channel_time([x_time, h_time, no])
y = self._demodulator(y_time)
elif self._domain == "freq":
# Frequency-domain simulations
cir = self._cdl(batch_size, self._rg.num_ofdm_symbols, 1/self._rg.ofdm_symbol_duration)
h_freq = cir_to_ofdm_channel(self._frequencies, *cir, normalize=True)
if self._direction == "downlink":
x_rg, g = self._zf_precoder([x_rg, h_freq])
y = self._channel_freq([x_rg, h_freq, no])
if self._perfect_csi:
if self._direction == "uplink":
h_hat = self._remove_nulled_scs(h_freq)
elif self._direction =="downlink":
h_hat = g
err_var = 0.0
else:
h_hat, err_var = self._ls_est ([y, no])
x_hat, no_eff = self._lmmse_equ([y, h_hat, err_var, no])
llr = self._demapper([x_hat, no_eff])
b_hat = self._decoder(llr)
return b, b_hat
Compare Uplink Performance Over the Different CDL Models
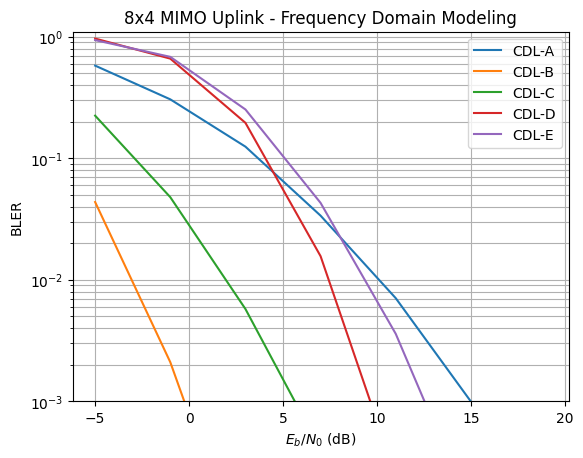
We will now compare the uplink performance over the various CDL models assuming perfect CSI at the receiver. Note that these simulations might take some time depending or you available hardware. You can reduce the batch_size if the model does not fit into the memory of your GPU. The code will also run on CPU if not GPU is available.
If you do not want to run the simulation your self, you skip the next cell and simply look at the result in the next cell.
[31]:
UL_SIMS = {
"ebno_db" : list(np.arange(-5, 20, 4.0)),
"cdl_model" : ["A", "B", "C", "D", "E"],
"delay_spread" : 100e-9,
"domain" : "freq",
"direction" : "uplink",
"perfect_csi" : True,
"speed" : 0.0,
"cyclic_prefix_length" : 6,
"pilot_ofdm_symbol_indices" : [2, 11],
"ber" : [],
"bler" : [],
"duration" : None
}
start = time.time()
for cdl_model in UL_SIMS["cdl_model"]:
model = Model(domain=UL_SIMS["domain"],
direction=UL_SIMS["direction"],
cdl_model=cdl_model,
delay_spread=UL_SIMS["delay_spread"],
perfect_csi=UL_SIMS["perfect_csi"],
speed=UL_SIMS["speed"],
cyclic_prefix_length=UL_SIMS["cyclic_prefix_length"],
pilot_ofdm_symbol_indices=UL_SIMS["pilot_ofdm_symbol_indices"])
ber, bler = sim_ber(model,
UL_SIMS["ebno_db"],
batch_size=256,
max_mc_iter=100,
num_target_block_errors=1000,
target_bler=1e-3)
UL_SIMS["ber"].append(list(ber.numpy()))
UL_SIMS["bler"].append(list(bler.numpy()))
UL_SIMS["duration"] = time.time() - start
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status
---------------------------------------------------------------------------------------------------------------------------------------
-5.0 | 1.1980e-01 | 5.7861e-01 | 176652 | 1474560 | 1185 | 2048 | 7.3 |reached target block errors
-1.0 | 5.5479e-02 | 3.0542e-01 | 163615 | 2949120 | 1251 | 4096 | 0.6 |reached target block errors
3.0 | 1.9751e-02 | 1.2463e-01 | 116495 | 5898240 | 1021 | 8192 | 1.2 |reached target block errors
7.0 | 5.1350e-03 | 3.3708e-02 | 109792 | 21381120 | 1001 | 29696 | 4.5 |reached target block errors
11.0 | 9.5245e-04 | 7.0605e-03 | 70222 | 73728000 | 723 | 102400 | 15.5 |reached max iter
15.0 | 1.1473e-04 | 9.9609e-04 | 8459 | 73728000 | 102 | 102400 | 15.5 |reached max iter
Simulation stopped as target BLER is reached @ EbNo = 15.0 dB.
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status
---------------------------------------------------------------------------------------------------------------------------------------
-5.0 | 6.0771e-03 | 4.3648e-02 | 103052 | 16957440 | 1028 | 23552 | 5.9 |reached target block errors
-1.0 | 2.4938e-04 | 2.0996e-03 | 18386 | 73728000 | 215 | 102400 | 15.4 |reached max iter
3.0 | 2.5228e-06 | 3.9063e-05 | 186 | 73728000 | 4 | 102400 | 15.4 |reached max iter
Simulation stopped as target BLER is reached @ EbNo = 3.0 dB.
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status
---------------------------------------------------------------------------------------------------------------------------------------
-5.0 | 3.8473e-02 | 2.2422e-01 | 141827 | 3686400 | 1148 | 5120 | 2.9 |reached target block errors
-1.0 | 7.3453e-03 | 4.7852e-02 | 113727 | 15482880 | 1029 | 21504 | 3.3 |reached target block errors
3.0 | 7.9734e-04 | 5.7520e-03 | 58786 | 73728000 | 589 | 102400 | 15.6 |reached max iter
7.0 | 4.9710e-05 | 4.0039e-04 | 3665 | 73728000 | 41 | 102400 | 15.6 |reached max iter
Simulation stopped as target BLER is reached @ EbNo = 7.0 dB.
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status
---------------------------------------------------------------------------------------------------------------------------------------
-5.0 | 2.1653e-01 | 9.6631e-01 | 319292 | 1474560 | 1979 | 2048 | 2.4 |reached target block errors
-1.0 | 1.1095e-01 | 6.6064e-01 | 163597 | 1474560 | 1353 | 2048 | 0.3 |reached target block errors
3.0 | 2.3986e-02 | 1.9570e-01 | 88423 | 3686400 | 1002 | 5120 | 0.7 |reached target block errors
7.0 | 1.5361e-03 | 1.5641e-02 | 71351 | 46448640 | 1009 | 64512 | 9.0 |reached target block errors
11.0 | 1.7008e-05 | 2.4414e-04 | 1254 | 73728000 | 25 | 102400 | 14.4 |reached max iter
Simulation stopped as target BLER is reached @ EbNo = 11.0 dB.
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status
---------------------------------------------------------------------------------------------------------------------------------------
-5.0 | 2.1054e-01 | 9.3848e-01 | 310448 | 1474560 | 1922 | 2048 | 2.4 |reached target block errors
-1.0 | 1.2151e-01 | 6.8311e-01 | 179170 | 1474560 | 1399 | 2048 | 0.3 |reached target block errors
3.0 | 3.4440e-02 | 2.5220e-01 | 101567 | 2949120 | 1033 | 4096 | 0.6 |reached target block errors
7.0 | 4.9954e-03 | 4.2926e-02 | 84709 | 16957440 | 1011 | 23552 | 3.3 |reached target block errors
11.0 | 3.4831e-04 | 3.5938e-03 | 25680 | 73728000 | 368 | 102400 | 14.4 |reached max iter
15.0 | 1.1366e-05 | 1.2695e-04 | 838 | 73728000 | 13 | 102400 | 14.4 |reached max iter
Simulation stopped as target BLER is reached @ EbNo = 15.0 dB.
[32]:
print("Simulation duration: {:1.2f} [h]".format(UL_SIMS["duration"]/3600))
plt.figure()
plt.xlabel(r"$E_b/N_0$ (dB)")
plt.ylabel("BLER")
plt.grid(which="both")
plt.title("8x4 MIMO Uplink - Frequency Domain Modeling");
plt.ylim([1e-3, 1.1])
legend = []
for i, bler in enumerate(UL_SIMS["bler"]):
plt.semilogy(UL_SIMS["ebno_db"], bler)
legend.append("CDL-{}".format(UL_SIMS["cdl_model"][i]))
plt.legend(legend);
Simulation duration: 0.05 [h]
Compare Downlink Performance Over the Different CDL Models
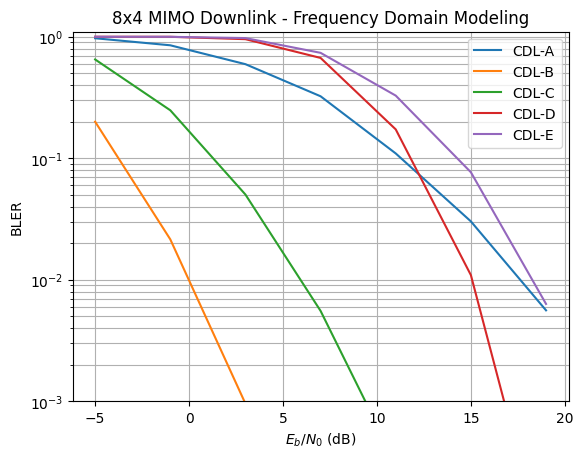
We will now compare the downlink performance over the various CDL models assuming perfect CSI at the receiver.
If you do not want to run the simulation your self, you skip the next cell and simply look at the result in the next cell.
[33]:
DL_SIMS = {
"ebno_db" : list(np.arange(-5, 20, 4.0)),
"cdl_model" : ["A", "B", "C", "D", "E"],
"delay_spread" : 100e-9,
"domain" : "freq",
"direction" : "downlink",
"perfect_csi" : True,
"speed" : 0.0,
"cyclic_prefix_length" : 6,
"pilot_ofdm_symbol_indices" : [2, 11],
"ber" : [],
"bler" : [],
"duration" : None
}
start = time.time()
for cdl_model in DL_SIMS["cdl_model"]:
model = Model(domain=DL_SIMS["domain"],
direction=DL_SIMS["direction"],
cdl_model=cdl_model,
delay_spread=DL_SIMS["delay_spread"],
perfect_csi=DL_SIMS["perfect_csi"],
speed=DL_SIMS["speed"],
cyclic_prefix_length=DL_SIMS["cyclic_prefix_length"],
pilot_ofdm_symbol_indices=DL_SIMS["pilot_ofdm_symbol_indices"])
ber, bler = sim_ber(model,
DL_SIMS["ebno_db"],
batch_size=256,
max_mc_iter=100,
num_target_block_errors=1000,
target_bler=1e-3)
DL_SIMS["ber"].append(list(ber.numpy()))
DL_SIMS["bler"].append(list(bler.numpy()))
DL_SIMS["duration"] = time.time() - start
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status
---------------------------------------------------------------------------------------------------------------------------------------
-5.0 | 3.5491e-01 | 9.7217e-01 | 523338 | 1474560 | 1991 | 2048 | 2.6 |reached target block errors
-1.0 | 2.7379e-01 | 8.5059e-01 | 403718 | 1474560 | 1742 | 2048 | 0.3 |reached target block errors
3.0 | 1.6478e-01 | 5.9473e-01 | 242976 | 1474560 | 1218 | 2048 | 0.3 |reached target block errors
7.0 | 8.0810e-02 | 3.2373e-01 | 238317 | 2949120 | 1326 | 4096 | 0.6 |reached target block errors
11.0 | 2.4725e-02 | 1.0959e-01 | 164061 | 6635520 | 1010 | 9216 | 1.3 |reached target block errors
15.0 | 6.0853e-03 | 3.0244e-02 | 148056 | 24330240 | 1022 | 33792 | 4.7 |reached target block errors
19.0 | 1.0188e-03 | 5.6055e-03 | 75116 | 73728000 | 574 | 102400 | 14.2 |reached max iter
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status
---------------------------------------------------------------------------------------------------------------------------------------
-5.0 | 3.5875e-02 | 2.0000e-01 | 132250 | 3686400 | 1024 | 5120 | 2.9 |reached target block errors
-1.0 | 3.4402e-03 | 2.1527e-02 | 116674 | 33914880 | 1014 | 47104 | 6.6 |reached target block errors
3.0 | 1.2263e-04 | 9.5703e-04 | 9041 | 73728000 | 98 | 102400 | 14.4 |reached max iter
Simulation stopped as target BLER is reached @ EbNo = 3.0 dB.
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status
---------------------------------------------------------------------------------------------------------------------------------------
-5.0 | 1.6116e-01 | 6.5039e-01 | 237637 | 1474560 | 1332 | 2048 | 2.5 |reached target block errors
-1.0 | 5.1945e-02 | 2.4829e-01 | 153191 | 2949120 | 1017 | 4096 | 0.6 |reached target block errors
3.0 | 9.2207e-03 | 5.0293e-02 | 135965 | 14745600 | 1030 | 20480 | 2.9 |reached target block errors
7.0 | 9.2376e-04 | 5.5469e-03 | 68107 | 73728000 | 568 | 102400 | 14.4 |reached max iter
11.0 | 5.1731e-05 | 3.1250e-04 | 3814 | 73728000 | 32 | 102400 | 14.5 |reached max iter
Simulation stopped as target BLER is reached @ EbNo = 11.0 dB.
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status
---------------------------------------------------------------------------------------------------------------------------------------
-5.0 | 4.1748e-01 | 1.0000e+00 | 307800 | 737280 | 1024 | 1024 | 2.7 |reached target block errors
-1.0 | 3.6758e-01 | 9.9902e-01 | 271011 | 737280 | 1023 | 1024 | 0.1 |reached target block errors
3.0 | 2.8536e-01 | 9.5508e-01 | 420781 | 1474560 | 1956 | 2048 | 0.3 |reached target block errors
7.0 | 1.4852e-01 | 6.6943e-01 | 219002 | 1474560 | 1371 | 2048 | 0.3 |reached target block errors
11.0 | 3.0268e-02 | 1.7285e-01 | 133897 | 4423680 | 1062 | 6144 | 0.8 |reached target block errors
15.0 | 1.5455e-03 | 1.0927e-02 | 102549 | 66355200 | 1007 | 92160 | 11.8 |reached target block errors
19.0 | 3.8113e-06 | 4.8828e-05 | 281 | 73728000 | 5 | 102400 | 13.1 |reached max iter
Simulation stopped as target BLER is reached @ EbNo = 19.0 dB.
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status
---------------------------------------------------------------------------------------------------------------------------------------
-5.0 | 4.2299e-01 | 1.0000e+00 | 311863 | 737280 | 1024 | 1024 | 2.3 |reached target block errors
-1.0 | 3.8418e-01 | 9.9902e-01 | 283246 | 737280 | 1023 | 1024 | 0.1 |reached target block errors
3.0 | 3.1512e-01 | 9.7510e-01 | 464663 | 1474560 | 1997 | 2048 | 0.3 |reached target block errors
7.0 | 1.9181e-01 | 7.3730e-01 | 282831 | 1474560 | 1510 | 2048 | 0.3 |reached target block errors
11.0 | 7.0917e-02 | 3.2780e-01 | 156858 | 2211840 | 1007 | 3072 | 0.4 |reached target block errors
15.0 | 1.3875e-02 | 7.6730e-02 | 143215 | 10321920 | 1100 | 14336 | 1.9 |reached target block errors
19.0 | 9.7339e-04 | 6.3281e-03 | 71766 | 73728000 | 648 | 102400 | 13.3 |reached max iter
[34]:
print("Simulation duration: {:1.2f} [h]".format(DL_SIMS["duration"]/3600))
plt.figure()
plt.xlabel(r"$E_b/N_0$ (dB)")
plt.ylabel("BLER")
plt.grid(which="both")
plt.title("8x4 MIMO Downlink - Frequency Domain Modeling");
plt.ylim([1e-3, 1.1])
legend = []
for i, bler in enumerate(DL_SIMS["bler"]):
plt.semilogy(DL_SIMS["ebno_db"], bler)
legend.append("CDL-{}".format(DL_SIMS["cdl_model"][i]))
plt.legend(legend);
Simulation duration: 0.04 [h]
Evaluate the Impact of Mobility
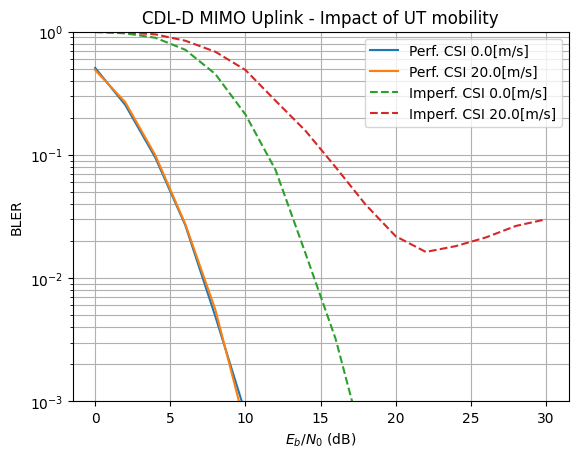
Let us now have a look at the impact of the UT speed on the uplink performance. We compare the scenarios of perfect and imperfect CSI and 0 m/s and 20 m/s speed. To amplify the detrimental effects of high mobility, we only configure a single OFDM symbol for pilot transmissions at the beginning of the resource grid. With perfect CSI, mobility plays hardly any role. However, once channel estimation is taken into acount, the BLER saturates.
If you do not want to run the simulation your self, you skip the next cell and simply look at the result in the next cell.
[35]:
MOBILITY_SIMS = {
"ebno_db" : list(np.arange(0, 32, 2.0)),
"cdl_model" : "D",
"delay_spread" : 100e-9,
"domain" : "freq",
"direction" : "uplink",
"perfect_csi" : [True, False],
"speed" : [0.0, 20.0],
"cyclic_prefix_length" : 6,
"pilot_ofdm_symbol_indices" : [0],
"ber" : [],
"bler" : [],
"duration" : None
}
start = time.time()
for perfect_csi in MOBILITY_SIMS["perfect_csi"]:
for speed in MOBILITY_SIMS["speed"]:
model = Model(domain=MOBILITY_SIMS["domain"],
direction=MOBILITY_SIMS["direction"],
cdl_model=MOBILITY_SIMS["cdl_model"],
delay_spread=MOBILITY_SIMS["delay_spread"],
perfect_csi=perfect_csi,
speed=speed,
cyclic_prefix_length=MOBILITY_SIMS["cyclic_prefix_length"],
pilot_ofdm_symbol_indices=MOBILITY_SIMS["pilot_ofdm_symbol_indices"])
ber, bler = sim_ber(model,
MOBILITY_SIMS["ebno_db"],
batch_size=256,
max_mc_iter=100,
num_target_block_errors=1000,
target_bler=1e-3)
MOBILITY_SIMS["ber"].append(list(ber.numpy()))
MOBILITY_SIMS["bler"].append(list(bler.numpy()))
MOBILITY_SIMS["duration"] = time.time() - start
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status
---------------------------------------------------------------------------------------------------------------------------------------
0.0 | 7.2941e-02 | 5.0879e-01 | 116519 | 1597440 | 1042 | 2048 | 2.4 |reached target block errors
2.0 | 3.1453e-02 | 2.5513e-01 | 100487 | 3194880 | 1045 | 4096 | 0.6 |reached target block errors
4.0 | 1.0154e-02 | 9.5348e-02 | 89216 | 8785920 | 1074 | 11264 | 1.6 |reached target block errors
6.0 | 2.5845e-03 | 2.6895e-02 | 76380 | 29552640 | 1019 | 37888 | 5.4 |reached target block errors
8.0 | 4.3472e-04 | 4.8828e-03 | 34722 | 79872000 | 500 | 102400 | 14.6 |reached max iter
10.0 | 6.2513e-05 | 8.0078e-04 | 4993 | 79872000 | 82 | 102400 | 14.7 |reached max iter
Simulation stopped as target BLER is reached @ EbNo = 10.0 dB.
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status
---------------------------------------------------------------------------------------------------------------------------------------
0.0 | 7.1526e-02 | 4.8828e-01 | 114259 | 1597440 | 1000 | 2048 | 2.8 |reached target block errors
2.0 | 3.3918e-02 | 2.6831e-01 | 108363 | 3194880 | 1099 | 4096 | 0.6 |reached target block errors
4.0 | 1.1292e-02 | 9.9707e-02 | 90189 | 7987200 | 1021 | 10240 | 1.5 |reached target block errors
6.0 | 2.7696e-03 | 2.7479e-02 | 79638 | 28753920 | 1013 | 36864 | 5.3 |reached target block errors
8.0 | 4.7170e-04 | 5.5371e-03 | 37676 | 79872000 | 567 | 102400 | 14.7 |reached max iter
10.0 | 4.2430e-05 | 6.2500e-04 | 3389 | 79872000 | 64 | 102400 | 14.7 |reached max iter
Simulation stopped as target BLER is reached @ EbNo = 10.0 dB.
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status
---------------------------------------------------------------------------------------------------------------------------------------
0.0 | 2.6250e-01 | 9.9316e-01 | 209664 | 798720 | 1017 | 1024 | 2.5 |reached target block errors
2.0 | 2.4348e-01 | 9.7021e-01 | 388951 | 1597440 | 1987 | 2048 | 0.3 |reached target block errors
4.0 | 2.0585e-01 | 8.9404e-01 | 328841 | 1597440 | 1831 | 2048 | 0.3 |reached target block errors
6.0 | 1.4910e-01 | 7.1387e-01 | 238180 | 1597440 | 1462 | 2048 | 0.3 |reached target block errors
8.0 | 8.4084e-02 | 4.5312e-01 | 201478 | 2396160 | 1392 | 3072 | 0.4 |reached target block errors
10.0 | 3.6994e-02 | 2.1289e-01 | 147740 | 3993600 | 1090 | 5120 | 0.7 |reached target block errors
12.0 | 1.2203e-02 | 7.5684e-02 | 136456 | 11182080 | 1085 | 14336 | 2.1 |reached target block errors
14.0 | 2.3083e-03 | 1.5830e-02 | 114308 | 49520640 | 1005 | 63488 | 9.2 |reached target block errors
16.0 | 4.4421e-04 | 3.2129e-03 | 35480 | 79872000 | 329 | 102400 | 14.8 |reached max iter
18.0 | 4.5360e-05 | 3.8086e-04 | 3623 | 79872000 | 39 | 102400 | 14.8 |reached max iter
Simulation stopped as target BLER is reached @ EbNo = 18.0 dB.
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status
---------------------------------------------------------------------------------------------------------------------------------------
0.0 | 2.7444e-01 | 9.9902e-01 | 219200 | 798720 | 1023 | 1024 | 2.4 |reached target block errors
2.0 | 2.5491e-01 | 9.8730e-01 | 203601 | 798720 | 1011 | 1024 | 0.1 |reached target block errors
4.0 | 2.3161e-01 | 9.5215e-01 | 369978 | 1597440 | 1950 | 2048 | 0.3 |reached target block errors
6.0 | 1.8989e-01 | 8.4521e-01 | 303343 | 1597440 | 1731 | 2048 | 0.3 |reached target block errors
8.0 | 1.4161e-01 | 6.8750e-01 | 226220 | 1597440 | 1408 | 2048 | 0.3 |reached target block errors
10.0 | 9.4019e-02 | 4.8926e-01 | 150190 | 1597440 | 1002 | 2048 | 0.3 |reached target block errors
12.0 | 4.8312e-02 | 2.7563e-01 | 154351 | 3194880 | 1129 | 4096 | 0.6 |reached target block errors
14.0 | 2.5432e-02 | 1.5681e-01 | 142189 | 5591040 | 1124 | 7168 | 1.0 |reached target block errors
16.0 | 1.1696e-02 | 7.9552e-02 | 121445 | 10383360 | 1059 | 13312 | 1.9 |reached target block errors
18.0 | 4.8950e-03 | 3.9453e-02 | 97744 | 19968000 | 1010 | 25600 | 3.7 |reached target block errors
20.0 | 2.0834e-03 | 2.1845e-02 | 76547 | 36741120 | 1029 | 47104 | 6.8 |reached target block errors
22.0 | 9.9547e-04 | 1.6325e-02 | 47706 | 47923200 | 1003 | 61440 | 8.9 |reached target block errors
24.0 | 9.5264e-04 | 1.8193e-02 | 41088 | 43130880 | 1006 | 55296 | 8.0 |reached target block errors
26.0 | 1.4505e-03 | 2.1399e-02 | 53294 | 36741120 | 1008 | 47104 | 6.8 |reached target block errors
28.0 | 2.0795e-03 | 2.6526e-02 | 61456 | 29552640 | 1005 | 37888 | 5.4 |reached target block errors
30.0 | 2.7439e-03 | 3.0037e-02 | 72324 | 26357760 | 1015 | 33792 | 4.9 |reached target block errors
[36]:
print("Simulation duration: {:1.2f} [h]".format(MOBILITY_SIMS["duration"]/3600))
plt.figure()
plt.xlabel(r"$E_b/N_0$ (dB)")
plt.ylabel("BLER")
plt.grid(which="both")
plt.title("CDL-D MIMO Uplink - Impact of UT mobility")
i = 0
for perfect_csi in MOBILITY_SIMS["perfect_csi"]:
for speed in MOBILITY_SIMS["speed"]:
style = "{}".format("-" if perfect_csi else "--")
s = "{} CSI {}[m/s]".format("Perf." if perfect_csi else "Imperf.", speed)
plt.semilogy(MOBILITY_SIMS["ebno_db"],
MOBILITY_SIMS["bler"][i],
style, label=s,)
i += 1
plt.legend();
plt.ylim([1e-3, 1]);
Simulation duration: 0.05 [h]
Evaluate the Impact of Insufficient Cyclic Prefix Length
As a final example, let us have a look at how to simulate OFDM with an insufficiently long cyclic prefix.
It is important to notice, that ISI cannot be simulated in the frequency domain as the OFDMChannel implicitly assumes perfectly synchronized and ISI-free transmissions. Having no cyclic prefix translates simply into an improved Eb/No as no energy for its transmission is used.
Simulating a channel in the time domain requires significantly more memory and compute which might limit the scenarios for which it can be used.
If you do not want to run the simulation your self, you skip the next cell and simply look at the result in the next cell.If you do not want to run the simulation your self, you skip the next cell and visualize the result in the next cell.
[37]:
CP_SIMS = {
"ebno_db" : list(np.arange(0, 17, 2.0)),
"cdl_model" : "C",
"delay_spread" : 100e-9,
"subcarrier_spacing" : 15e3,
"domain" : ["freq", "time"],
"direction" : "uplink",
"perfect_csi" : False,
"speed" : 3.0,
"cyclic_prefix_length" : [20, 2],
"pilot_ofdm_symbol_indices" : [2, 11],
"ber" : [],
"bler" : [],
"duration": None
}
start = time.time()
for cyclic_prefix_length in CP_SIMS["cyclic_prefix_length"]:
for domain in CP_SIMS["domain"]:
model = Model(domain=domain,
direction=CP_SIMS["direction"],
cdl_model=CP_SIMS["cdl_model"],
delay_spread=CP_SIMS["delay_spread"],
perfect_csi=CP_SIMS["perfect_csi"],
speed=CP_SIMS["speed"],
cyclic_prefix_length=cyclic_prefix_length,
pilot_ofdm_symbol_indices=CP_SIMS["pilot_ofdm_symbol_indices"],
subcarrier_spacing=CP_SIMS["subcarrier_spacing"])
ber, bler = sim_ber(model,
CP_SIMS["ebno_db"],
batch_size=64,
max_mc_iter=1000,
num_target_block_errors=1000,
target_bler=1e-3)
CP_SIMS["ber"].append(list(ber.numpy()))
CP_SIMS["bler"].append(list(bler.numpy()))
CP_SIMS["duration"] = time.time() - start
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status
---------------------------------------------------------------------------------------------------------------------------------------
0.0 | 6.6023e-02 | 3.1100e-01 | 158201 | 2396160 | 1035 | 3328 | 3.5 |reached target block errors
2.0 | 3.2979e-02 | 1.6437e-01 | 151967 | 4608000 | 1052 | 6400 | 1.6 |reached target block errors
4.0 | 1.3858e-02 | 7.3998e-02 | 135383 | 9768960 | 1004 | 13568 | 3.3 |reached target block errors
6.0 | 5.4884e-03 | 2.9576e-02 | 134546 | 24514560 | 1007 | 34048 | 8.4 |reached target block errors
8.0 | 1.9573e-03 | 1.1077e-02 | 127352 | 65064960 | 1001 | 90368 | 22.2 |reached target block errors
10.0 | 6.2485e-04 | 3.5820e-03 | 115173 | 184320000 | 917 | 256000 | 63.0 |reached max iter
12.0 | 1.6797e-04 | 9.6875e-04 | 30960 | 184320000 | 248 | 256000 | 63.0 |reached max iter
Simulation stopped as target BLER is reached @ EbNo = 12.0 dB.
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status
---------------------------------------------------------------------------------------------------------------------------------------
0.0 | 6.2418e-02 | 2.9688e-01 | 161069 | 2580480 | 1064 | 3584 | 5.3 |reached target block errors
2.0 | 3.2143e-02 | 1.6016e-01 | 148113 | 4608000 | 1025 | 6400 | 4.3 |reached target block errors
4.0 | 1.4416e-02 | 7.5346e-02 | 138169 | 9584640 | 1003 | 13312 | 8.9 |reached target block errors
6.0 | 5.7455e-03 | 3.0819e-02 | 134495 | 23408640 | 1002 | 32512 | 21.7 |reached target block errors
8.0 | 1.8941e-03 | 1.0892e-02 | 125337 | 66170880 | 1001 | 91904 | 61.3 |reached target block errors
10.0 | 6.0567e-04 | 3.5547e-03 | 111638 | 184320000 | 910 | 256000 | 170.6 |reached max iter
12.0 | 1.5749e-04 | 9.5312e-04 | 29029 | 184320000 | 244 | 256000 | 170.3 |reached max iter
Simulation stopped as target BLER is reached @ EbNo = 12.0 dB.
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status
---------------------------------------------------------------------------------------------------------------------------------------
0.0 | 4.4475e-02 | 2.2005e-01 | 147556 | 3317760 | 1014 | 4608 | 3.4 |reached target block errors
2.0 | 2.2355e-02 | 1.1529e-01 | 144218 | 6451200 | 1033 | 8960 | 2.2 |reached target block errors
4.0 | 8.9747e-03 | 4.8418e-02 | 133991 | 14929920 | 1004 | 20736 | 5.1 |reached target block errors
6.0 | 3.4489e-03 | 1.9590e-02 | 127140 | 36864000 | 1003 | 51200 | 12.7 |reached target block errors
8.0 | 1.2003e-03 | 6.9383e-03 | 124553 | 103772160 | 1000 | 144128 | 35.8 |reached target block errors
10.0 | 3.3025e-04 | 1.9727e-03 | 60871 | 184320000 | 505 | 256000 | 63.3 |reached max iter
12.0 | 9.0587e-05 | 5.2344e-04 | 16697 | 184320000 | 134 | 256000 | 63.4 |reached max iter
Simulation stopped as target BLER is reached @ EbNo = 12.0 dB.
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status
---------------------------------------------------------------------------------------------------------------------------------------
0.0 | 1.1673e-01 | 5.2148e-01 | 172125 | 1474560 | 1068 | 2048 | 4.0 |reached target block errors
2.0 | 8.0832e-02 | 3.7997e-01 | 163888 | 2027520 | 1070 | 2816 | 1.6 |reached target block errors
4.0 | 4.5935e-02 | 2.2743e-01 | 152402 | 3317760 | 1048 | 4608 | 2.7 |reached target block errors
6.0 | 2.4481e-02 | 1.2639e-01 | 139883 | 5713920 | 1003 | 7936 | 4.6 |reached target block errors
8.0 | 1.1186e-02 | 6.0637e-02 | 134020 | 11980800 | 1009 | 16640 | 9.7 |reached target block errors
10.0 | 5.1637e-03 | 2.8809e-02 | 129440 | 25067520 | 1003 | 34816 | 20.3 |reached target block errors
12.0 | 1.9280e-03 | 1.2601e-02 | 110162 | 57139200 | 1000 | 79360 | 46.3 |reached target block errors
14.0 | 6.6189e-04 | 6.8479e-03 | 69662 | 105246720 | 1001 | 146176 | 85.2 |reached target block errors
16.0 | 2.2316e-04 | 6.1419e-03 | 26160 | 117227520 | 1000 | 162816 | 94.9 |reached target block errors
[38]:
print("Simulation duration: {:1.2f} [h]".format(CP_SIMS["duration"]/3600))
plt.figure()
plt.xlabel(r"$E_b/N_0$ (dB)")
plt.ylabel("BLER")
plt.grid(which="both")
plt.title("CDL-B MIMO Uplink - Impact of Cyclic Prefix Length")
i = 0
for cyclic_prefix_length in CP_SIMS["cyclic_prefix_length"]:
for domain in CP_SIMS["domain"]:
s = "{} Domain, CP length: {}".format("Freq" if domain=="freq" else "Time",
cyclic_prefix_length)
plt.semilogy(CP_SIMS["ebno_db"],
CP_SIMS["bler"][i],
label=s)
i += 1
plt.legend();
plt.ylim([1e-3, 1]);
Simulation duration: 0.30 [h]
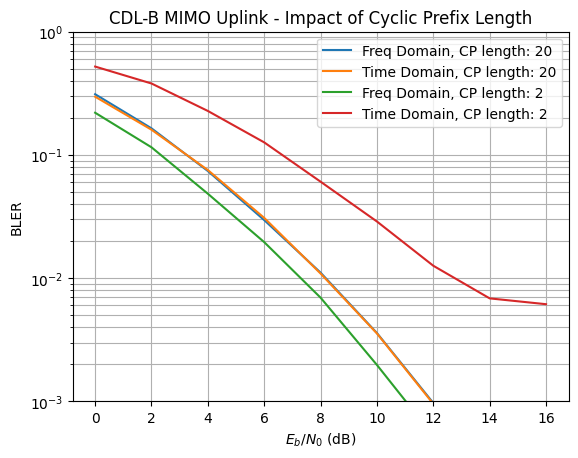
One can make a few important observations from the figure above:
The length of the cyclic prefix has no impact on the performance if the system is simulated in the frequency domain. The reason why the two curves for both frequency-domain simulations do not overlap is that the cyclic prefix length affects the way the Eb/No is computed.
With a sufficiently large cyclic prefix (in our case
cyclic_prefix_length = 20 >= l_tot = 17), the performance of time and frequency-domain simulations are identical.With a too small cyclic prefix length, the performance degrades. At high SNR, inter-symbol interference (from multiple streams) becomes the dominating source of interference.