OFDM MIMO Channel Estimation and Detection
In this notebook, we will evaluate some of the OFDM channel estimation and MIMO detection algorithms available in Sionna.
We will start by evaluating the mean square error (MSE) preformance of various channel estimation and interpolation methods.
Then, we will compare some of the MIMO detection algorithms under both perfect and imperfect channel state information (CSI) in terms of uncoded symbol error rate (SER) and coded bit error rate (BER).
The developed end-to-end Keras models in this notebook are a great tool for benchmarking of MIMO receivers under realistic conditions. They can be easily extended to new channel estimation methods or MIMO detection algorithms.
For MSE evaluations, the block diagram of the system looks as follows:
where the channel estimation module is highlighted as it is the focus of this evaluation. The channel covariance matrices are required for linear minimum mean square error (LMMSE) channel interpolation.
For uncoded SER evaluations, the block diagram of the system looks as follows:
where the channel estimation and detection modules are highlighted as they are the focus of this evaluation.
Finally, for coded BER evaluations, the block diagram of the system looks as follows:
Table of Contents
GPU Configuration and Imports
[1]:
import os
if os.getenv("CUDA_VISIBLE_DEVICES") is None:
gpu_num = 0 # Use "" to use the CPU
os.environ["CUDA_VISIBLE_DEVICES"] = f"{gpu_num}"
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '3'
# Import Sionna
try:
import sionna
except ImportError as e:
# Install Sionna if package is not already installed
import os
os.system("pip install sionna")
import sionna
# Configure the notebook to use only a single GPU and allocate only as much memory as needed
# For more details, see https://www.tensorflow.org/guide/gpu
import tensorflow as tf
gpus = tf.config.list_physical_devices('GPU')
if gpus:
try:
tf.config.experimental.set_memory_growth(gpus[0], True)
except RuntimeError as e:
print(e)
# Avoid warnings from TensorFlow
tf.get_logger().setLevel('ERROR')
sionna.config.seed = 42 # Set seed for reproducible random number generation
[2]:
%matplotlib inline
import matplotlib.pyplot as plt
import numpy as np
import pickle
from tensorflow.keras import Model
from sionna.mimo import StreamManagement
from sionna.utils import QAMSource, compute_ser, BinarySource, sim_ber, ebnodb2no, QAMSource
from sionna.mapping import Mapper
from sionna.ofdm import ResourceGrid, ResourceGridMapper, LSChannelEstimator, LMMSEInterpolator, LinearDetector, KBestDetector, EPDetector, MMSEPICDetector
from sionna.channel import GenerateOFDMChannel, OFDMChannel, gen_single_sector_topology
from sionna.channel.tr38901 import UMi, Antenna, PanelArray
from sionna.fec.ldpc import LDPC5GEncoder
from sionna.fec.ldpc import LDPC5GDecoder
Simulation parameters
The next cell defines the simulation parameters used throughout this notebook.
This includes the OFDM waveform parameters, antennas geometries and patterns, and the 3GPP UMi channel model.
[3]:
NUM_OFDM_SYMBOLS = 14
FFT_SIZE = 12*4 # 4 PRBs
SUBCARRIER_SPACING = 30e3 # Hz
CARRIER_FREQUENCY = 3.5e9 # Hz
SPEED = 3. # m/s
# The user terminals (UTs) are equipped with a single antenna
# with vertial polarization.
UT_ANTENNA = Antenna(polarization='single',
polarization_type='V',
antenna_pattern='omni', # Omnidirectional antenna pattern
carrier_frequency=CARRIER_FREQUENCY)
# The base station is equipped with an antenna
# array of 8 cross-polarized antennas,
# resulting in a total of 16 antenna elements.
NUM_RX_ANT = 16
BS_ARRAY = PanelArray(num_rows_per_panel=4,
num_cols_per_panel=2,
polarization='dual',
polarization_type='cross',
antenna_pattern='38.901', # 3GPP 38.901 antenna pattern
carrier_frequency=CARRIER_FREQUENCY)
# 3GPP UMi channel model is considered
CHANNEL_MODEL = UMi(carrier_frequency=CARRIER_FREQUENCY,
o2i_model='low',
ut_array=UT_ANTENNA,
bs_array=BS_ARRAY,
direction='uplink',
enable_shadow_fading=False,
enable_pathloss=False)
Estimation of the channel time, frequency, and spatial covariance matrices
The linear minimum mean square (LMMSE) interpolation method requires knowledge of the time (i.e., across OFDM symbols), frequency (i.e., across sub-carriers), and spatial (i.e., across receive antennas) covariance matrices of the channel frequency response.
These are estimated in this section using Monte Carlo sampling.
We explain below how this is achieved for the frequency covariance matrix. The same approach is used for the time and spatial covariance matrices.
Let \(N\) be the number of sub-carriers. The first step for estimating the frequency covariance matrix is to sample the channel model in order to build a set of frequency-domain channel realizations \(\left\{ \mathbf{h}_k \right\}, 1 \leq k \leq K\), where \(K\) is the number of samples and \(\mathbf{h}_k \in \mathbb{C}^{N}\) are complex-valued samples of the channel frequency response.
The frequency covariance matrix \(\mathbf{R}^{(f)} \in \mathbb{C}^{N \times N}\) is then estimated by
\begin{equation} \mathbf{R}^{(f)} \approx \frac{1}{K} \sum_{k = 1}^K \mathbf{h}_k \mathbf{h}_k^{\mathrm{H}} \end{equation}
where we assume that the frequency-domain channel response has zero mean.
The following cells implement this process for all three dimensions (frequency, time, and space).
The next cell defines a resource grid and an OFDM channel generator for sampling the channel in the frequency domain.
[4]:
rg = ResourceGrid(num_ofdm_symbols=NUM_OFDM_SYMBOLS,
fft_size=FFT_SIZE,
subcarrier_spacing=SUBCARRIER_SPACING)
channel_sampler = GenerateOFDMChannel(CHANNEL_MODEL, rg)
Then, a function that samples the channel is defined. It randomly samples a network topology for every batch and for every batch example using the appropriate utility function.
[5]:
def sample_channel(batch_size):
# Sample random topologies
topology = gen_single_sector_topology(batch_size, 1, 'umi', min_ut_velocity=SPEED, max_ut_velocity=SPEED)
CHANNEL_MODEL.set_topology(*topology)
# Sample channel frequency responses
# [batch size, 1, num_rx_ant, 1, 1, num_ofdm_symbols, fft_size]
h_freq = channel_sampler(batch_size)
# [batch size, num_rx_ant, num_ofdm_symbols, fft_size]
h_freq = h_freq[:,0,:,0,0]
return h_freq
We now define a function that estimates the frequency, time, and spatial covariance matrcies using Monte Carlo sampling.
[6]:
@tf.function(jit_compile=True) # Use XLA for speed-up
def estimate_covariance_matrices(num_it, batch_size):
freq_cov_mat = tf.zeros([FFT_SIZE, FFT_SIZE], tf.complex64)
time_cov_mat = tf.zeros([NUM_OFDM_SYMBOLS, NUM_OFDM_SYMBOLS], tf.complex64)
space_cov_mat = tf.zeros([NUM_RX_ANT, NUM_RX_ANT], tf.complex64)
for _ in tf.range(num_it):
# [batch size, num_rx_ant, num_ofdm_symbols, fft_size]
h_samples = sample_channel(batch_size)
#################################
# Estimate frequency covariance
#################################
# [batch size, num_rx_ant, fft_size, num_ofdm_symbols]
h_samples_ = tf.transpose(h_samples, [0,1,3,2])
# [batch size, num_rx_ant, fft_size, fft_size]
freq_cov_mat_ = tf.matmul(h_samples_, h_samples_, adjoint_b=True)
# [fft_size, fft_size]
freq_cov_mat_ = tf.reduce_mean(freq_cov_mat_, axis=(0,1))
# [fft_size, fft_size]
freq_cov_mat += freq_cov_mat_
################################
# Estimate time covariance
################################
# [batch size, num_rx_ant, num_ofdm_symbols, fft_size]
time_cov_mat_ = tf.matmul(h_samples, h_samples, adjoint_b=True)
# [num_ofdm_symbols, num_ofdm_symbols]
time_cov_mat_ = tf.reduce_mean(time_cov_mat_, axis=(0,1))
# [num_ofdm_symbols, num_ofdm_symbols]
time_cov_mat += time_cov_mat_
###############################
# Estimate spatial covariance
###############################
# [batch size, num_ofdm_symbols, num_rx_ant, fft_size]
h_samples_ = tf.transpose(h_samples, [0,2,1,3])
# [batch size, num_ofdm_symbols, num_rx_ant, num_rx_ant]
space_cov_mat_ = tf.matmul(h_samples_, h_samples_, adjoint_b=True)
# [num_rx_ant, num_rx_ant]
space_cov_mat_ = tf.reduce_mean(space_cov_mat_, axis=(0,1))
# [num_rx_ant, num_rx_ant]
space_cov_mat += space_cov_mat_
freq_cov_mat /= tf.complex(tf.cast(NUM_OFDM_SYMBOLS*num_it, tf.float32), 0.0)
time_cov_mat /= tf.complex(tf.cast(FFT_SIZE*num_it, tf.float32), 0.0)
space_cov_mat /= tf.complex(tf.cast(FFT_SIZE*num_it, tf.float32), 0.0)
return freq_cov_mat, time_cov_mat, space_cov_mat
We then compute the estimates by executing the function defined in the previous cell.
The batch size and number of iterations determine the total number of samples, i.e.,
number of samples = batch_size x num_iterations
and hence control the tradeoff between the accuracy of the estimates and the time needed for their computation.
[7]:
batch_size = 1000
num_iterations = 100
sionna.config.xla_compat = True # Enable Sionna's support of XLA
FREQ_COV_MAT, TIME_COV_MAT, SPACE_COV_MAT = estimate_covariance_matrices(batch_size, num_iterations)
sionna.config.xla_compat = False # Disable Sionna's support of XLA
/home/jhoydis/.local/lib/python3.10/site-packages/sionna/config.py:164: UserWarning: XLA can lead to reduced numerical precision. Use with care.
warnings.warn(msg)
WARNING: All log messages before absl::InitializeLog() is called are written to STDERR
I0000 00:00:1727264741.860667 75100 device_compiler.h:186] Compiled cluster using XLA! This line is logged at most once for the lifetime of the process.
Finally, the estimated matrices are saved (as numpy arrays) for future use.
[9]:
# FREQ_COV_MAT : [fft_size, fft_size]
# TIME_COV_MAT : [num_ofdm_symbols, num_ofdm_symbols]
# SPACE_COV_MAT : [num_rx_ant, num_rx_ant]
np.save('freq_cov_mat', FREQ_COV_MAT.numpy())
np.save('time_cov_mat', TIME_COV_MAT.numpy())
np.save('space_cov_mat', SPACE_COV_MAT.numpy())
Loading the channel covariance matrices
The next cell loads saved estimates of the time, frequency, and space covariance matrices.
[10]:
FREQ_COV_MAT = np.load('freq_cov_mat.npy')
TIME_COV_MAT = np.load('time_cov_mat.npy')
SPACE_COV_MAT = np.load('space_cov_mat.npy')
We then visualize the loaded matrices.
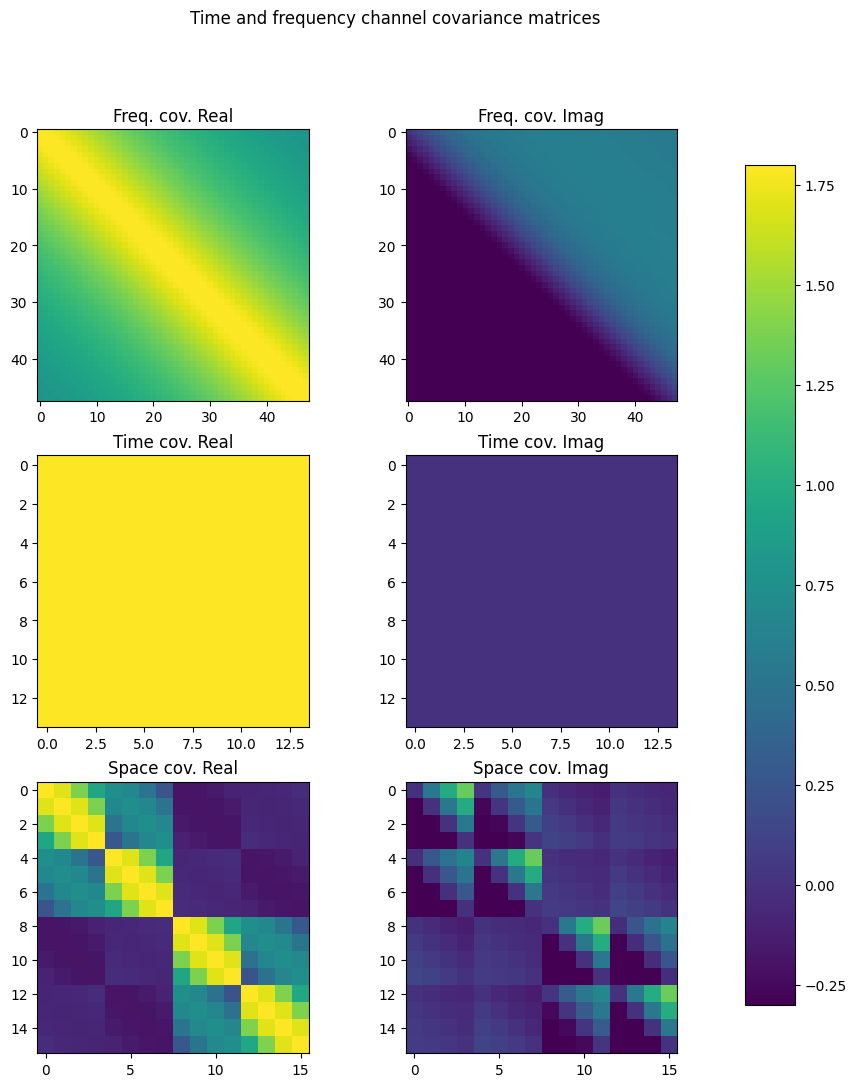
As one can see, the frequency correlation slowly decays with increasing spectral distance.
The time-correlation is much stronger as the mobility low. The covariance matrix is hence very badly conditioned with rank almost equal to one.
The spatial covariance matrix has a regular structure which is determined by the array geometry and polarization of its elements.
[11]:
fig, ax = plt.subplots(3,2, figsize=(10,12))
fig.suptitle("Time and frequency channel covariance matrices")
ax[0,0].set_title("Freq. cov. Real")
im = ax[0,0].imshow(FREQ_COV_MAT.real, vmin=-0.3, vmax=1.8)
ax[0,1].set_title("Freq. cov. Imag")
im = ax[0,1].imshow(FREQ_COV_MAT.imag, vmin=-0.3, vmax=1.8)
ax[1,0].set_title("Time cov. Real")
im = ax[1,0].imshow(TIME_COV_MAT.real, vmin=-0.3, vmax=1.8)
ax[1,1].set_title("Time cov. Imag")
im = ax[1,1].imshow(TIME_COV_MAT.imag, vmin=-0.3, vmax=1.8)
ax[2,0].set_title("Space cov. Real")
im = ax[2,0].imshow(SPACE_COV_MAT.real, vmin=-0.3, vmax=1.8)
ax[2,1].set_title("Space cov. Imag")
im = ax[2,1].imshow(SPACE_COV_MAT.imag, vmin=-0.3, vmax=1.8)
fig.subplots_adjust(right=0.8)
cbar_ax = fig.add_axes([0.85, 0.15, 0.05, 0.7])
fig.colorbar(im, cax=cbar_ax);
Comparison of OFDM estimators
This section focuses on comparing the available OFDM channel estimators in Sionna for the considered setup.
OFDM channel estimation consists of two steps:
Channel estimation at pilot-carrying resource elements using least-squares (LS).
Interpolation for data-carrying resource elements, for which three methods are available in Sionna:
Nearest-neighbor, which uses the channel estimate of the nearest pilot
Linear, with optional averaging over the OFDM symbols (time dimension) for low mobility scenarios
LMMSE, which requires knowledge of the time and frequency covariance matrices
The LMMSE interpolator also features optional spatial smoothin, which requires the spatial covarance matrix. The API documentation explains in more detail how this interpolator operates.
End-to-end model
In the next cell, we will create a Keras model which uses the interpolation method specified at initialization.
It computes the mean square error (MSE) for a specified batch size and signal-to-noise ratio (SNR) (in dB).
The following interpolation methods are available (set through the int_method parameter):
"nn": Nearest-neighbor interpolation"lin": Linear interpolation"lmmse": LMMSE interpolation
When LMMSE interpolation is used, it is required to specified the order in which interpolation and optional spatial smoothing is performed. This is achieved using the lmmse_order parameter. For example, setting this parameter to "f-t" leads to frequency interpolation being performed first followed by time interpolation, and no spatial smoothing. Setting it to "t-f-s" leads to time interpolation being performed first, followed by frequency interpolation, and finally spatial smoothing.
[12]:
class MIMOOFDMLink(Model):
def __init__(self, int_method, lmmse_order=None, **kwargs):
super().__init__(kwargs)
assert int_method in ('nn', 'lin', 'lmmse')
# Configure the resource grid
rg = ResourceGrid(num_ofdm_symbols=NUM_OFDM_SYMBOLS,
fft_size=FFT_SIZE,
subcarrier_spacing=SUBCARRIER_SPACING,
num_tx=1,
pilot_pattern="kronecker",
pilot_ofdm_symbol_indices=[2,11])
self.rg = rg
# Stream management
# Only a sinlge UT is considered for channel estimation
sm = StreamManagement([[1]], 1)
##################################
# Transmitter
##################################
self.qam_source = QAMSource(num_bits_per_symbol=2) # Modulation order does not impact the channel estimation. Set to QPSK
self.rg_mapper = ResourceGridMapper(rg)
##################################
# Channel
##################################
self.channel = OFDMChannel(CHANNEL_MODEL, rg, return_channel=True)
###################################
# Receiver
###################################
# Channel estimation
freq_cov_mat = tf.constant(FREQ_COV_MAT, tf.complex64)
time_cov_mat = tf.constant(TIME_COV_MAT, tf.complex64)
space_cov_mat = tf.constant(SPACE_COV_MAT, tf.complex64)
if int_method == 'nn':
self.channel_estimator = LSChannelEstimator(rg, interpolation_type='nn')
elif int_method == 'lin':
self.channel_estimator = LSChannelEstimator(rg, interpolation_type='lin')
elif int_method == 'lmmse':
lmmse_int_freq_first = LMMSEInterpolator(rg.pilot_pattern, time_cov_mat, freq_cov_mat, space_cov_mat, order=lmmse_order)
self.channel_estimator = LSChannelEstimator(rg, interpolator=lmmse_int_freq_first)
@tf.function
def call(self, batch_size, snr_db):
##################################
# Transmitter
##################################
x = self.qam_source([batch_size, 1, 1, self.rg.num_data_symbols])
x_rg = self.rg_mapper(x)
##################################
# Channel
##################################
no = tf.pow(10.0, -snr_db/10.0)
topology = gen_single_sector_topology(batch_size, 1, 'umi', min_ut_velocity=SPEED, max_ut_velocity=SPEED)
CHANNEL_MODEL.set_topology(*topology)
y_rg, h_freq = self.channel((x_rg, no))
###################################
# Channel estimation
###################################
h_hat,_ = self.channel_estimator((y_rg,no))
###################################
# MSE
###################################
mse = tf.reduce_mean(tf.square(tf.abs(h_freq-h_hat)))
return mse
The next cell defines a function for evaluating the mean square error (MSE) of a model over a range of SNRs (snr_dbs).
The batch_size and num_it parameters control the number of samples used to compute the MSE for each SNR value.
[13]:
def evaluate_mse(model, snr_dbs, batch_size, num_it):
# Casting model inputs to TensorFlow types to avoid
# re-building of the graph
snr_dbs = tf.cast(snr_dbs, tf.float32)
batch_size = tf.cast(batch_size, tf.int32)
mses = []
for snr_db in snr_dbs:
mse_ = 0.0
for _ in range(num_it):
mse_ += model(batch_size, snr_db).numpy()
# Averaging over the number of iterations
mse_ /= float(num_it)
mses.append(mse_)
return mses
The next cell defines the evaluation parameters.
[14]:
# Range of SNR (in dB)
SNR_DBs = np.linspace(-10.0, 20.0, 20)
# Number of iterations and batch size.
# These parameters control the number of samples used to compute each SNR value.
# The higher the number of samples is, the more accurate the MSE estimation is, at
# the cost of longer compute time.
BATCH_SIZE = 512
NUM_IT = 10
# Interpolation/filtering order for the LMMSE interpolator.
# All valid configurations are listed.
# Some are commented to speed-up simulations.
# Uncomment configurations to evaluate them!
ORDERS = ['s-t-f', # Space - time - frequency
#'s-f-t', # Space - frequency - time
#'t-s-f', # Time - space - frequency
't-f-s', # Time - frequency - space
#'f-t-s', # Frequency - time - space
#'f-s-t', # Frequency - space- time
#'f-t', # Frequency - time (no spatial smoothing)
't-f' # Time - frequency (no spatial smoothing)
]
The next cell evaluates the nearest-neighbor, linear, and LMMSE interpolator. For the LMMSE interpolator, we loop through the configuration listed in ORDERS.
[15]:
MSES = {}
# Nearest-neighbor interpolation
e2e = MIMOOFDMLink("nn")
MSES['nn'] = evaluate_mse(e2e, SNR_DBs, BATCH_SIZE, NUM_IT)
# Linear interpolation
e2e = MIMOOFDMLink("lin")
MSES['lin'] = evaluate_mse(e2e, SNR_DBs, BATCH_SIZE, NUM_IT)
# LMMSE
for order in ORDERS:
e2e = MIMOOFDMLink("lmmse", order)
MSES[f"lmmse: {order}"] = evaluate_mse(e2e, SNR_DBs, BATCH_SIZE, NUM_IT)
Finally, we plot the MSE.
[16]:
plt.figure(figsize=(8,6))
for est_label in MSES:
plt.semilogy(SNR_DBs, MSES[est_label], label=est_label)
plt.xlabel(r"SNR (dB)")
plt.ylabel("MSE")
plt.legend()
plt.grid(True)
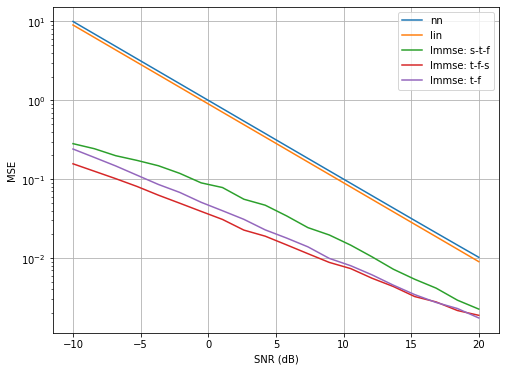
Unsurprisingly, the LMMSE interpolator leads to more accurate estimates compared to the two other methods, as it leverages knowledge of the the channel statistics. Moreover, the order in which the LMMSE interpolation steps are performed strongly impacts the accuracy of the estimator. This is because the LMMSE interpolation operates in one dimension at a time which is not equivalent to full-blown LMMSE estimation across all dimensions at one.
Also note that the order that leads to the best accuracy depends on the channel statistics. As a rule of thumb, it might be good to start with the dimension that is most strongly correlated (i.e., time in our example).
Comparison of MIMO detectors
An OFDM MIMO receiver consists of two stages: OFDM channel estimation and MIMO detection.
While the previous section focused on OFDM channel estimation, this section focuses now on MIMO detection.
The following MIMO detection algorithms, all available out-of-the-box in Sionna, are considered:
Both perfect and imperfect channel state information is considered in the simulations. LS estimation combined with LMMSE interpolation is used, with time-frequency-space smoothing (in this order, i.e., order='t-f-s').
End-to-end model
A Keras model is created in the next cell, which uses the detection method specified at initialization.
It computes either the coded bit error rate (BER) or the uncoded symbol error rate (SER), for a specified batch size, \(E_b/N_0\) (in dB), and QAM modulation with a specified modulation order. When computing the BER, a 5G LDPC code is used with the specified coderate.
The following MIMO detection methods are considered (set through the det_param parameter):
"lmmse": No parameter needed"k-best": List sizek, defaults to 64"ep": Number of iterationsl, defaults to 10"mmse-pic": Number of self-iterationsnum_it, defaults to 4
The det_param parameter corresponds to either k, l, or num_it, for K-Best, EP, or MMSE-PIC, respectively. If set to None, a default value is used according to the selected detector.
The perf_csi parameter controls whether perfect CSI is assumed or not. If set to False, then LS combined with LMMSE interpolation is used to estimate the channel.
You can easily add your own MIMO detector and channel estimator to this model for a fair and realistic benchmark.
[17]:
class MIMOOFDMLink(Model):
def __init__(self, output, det_method, perf_csi, num_tx, num_bits_per_symbol, det_param=None, coderate=0.5, **kwargs):
super().__init__(kwargs)
assert det_method in ('lmmse', 'k-best', 'ep', 'mmse-pic'), "Unknown detection method"
self._output = output
self.num_tx = num_tx
self.num_bits_per_symbol = num_bits_per_symbol
self.coderate = coderate
self.det_method = det_method
self.perf_csi = perf_csi
# Configure the resource grid
rg = ResourceGrid(num_ofdm_symbols=NUM_OFDM_SYMBOLS,
fft_size=FFT_SIZE,
subcarrier_spacing=SUBCARRIER_SPACING,
num_tx=num_tx,
pilot_pattern="kronecker",
pilot_ofdm_symbol_indices=[2,11])
self.rg = rg
# Stream management
sm = StreamManagement(np.ones([1,num_tx], int), 1)
# Codeword length and number of information bits per codeword
n = int(rg.num_data_symbols*num_bits_per_symbol)
k = int(coderate*n)
self.n = n
self.k = k
# If output is symbol, then no FEC is used and hard decision are output
hard_out = (output == "symbol")
coded = (output == "bit")
self.hard_out = hard_out
self.coded = coded
##################################
# Transmitter
##################################
self.binary_source = BinarySource()
self.mapper = Mapper(constellation_type="qam", num_bits_per_symbol=num_bits_per_symbol, return_indices=True)
self.rg_mapper = ResourceGridMapper(rg)
if coded:
self.encoder = LDPC5GEncoder(k, n, num_bits_per_symbol=num_bits_per_symbol)
##################################
# Channel
##################################
self.channel = OFDMChannel(CHANNEL_MODEL, rg, return_channel=True)
###################################
# Receiver
###################################
# Channel estimation
if not self.perf_csi:
freq_cov_mat = tf.constant(FREQ_COV_MAT, tf.complex64)
time_cov_mat = tf.constant(TIME_COV_MAT, tf.complex64)
space_cov_mat = tf.constant(SPACE_COV_MAT, tf.complex64)
lmmse_int_time_first = LMMSEInterpolator(rg.pilot_pattern, time_cov_mat, freq_cov_mat, space_cov_mat, order='t-f-s')
self.channel_estimator = LSChannelEstimator(rg, interpolator=lmmse_int_time_first)
# Detection
if det_method == "lmmse":
self.detector = LinearDetector("lmmse", output, "app", rg, sm, constellation_type="qam", num_bits_per_symbol=num_bits_per_symbol, hard_out=hard_out)
elif det_method == 'k-best':
if det_param is None:
k = 64
else:
k = det_param
self.detector = KBestDetector(output, num_tx, k, rg, sm, constellation_type="qam", num_bits_per_symbol=num_bits_per_symbol, hard_out=hard_out)
elif det_method == "ep":
if det_param is None:
l = 10
else:
l = det_param
self.detector = EPDetector(output, rg, sm, num_bits_per_symbol, l=l, hard_out=hard_out)
elif det_method == 'mmse-pic':
if det_param is None:
l = 4
else:
l = det_param
self.detector = MMSEPICDetector(output, rg, sm, 'app', num_iter=l, constellation_type="qam", num_bits_per_symbol=num_bits_per_symbol, hard_out=hard_out)
if coded:
self.decoder = LDPC5GDecoder(self.encoder, hard_out=False)
@tf.function
def call(self, batch_size, ebno_db):
##################################
# Transmitter
##################################
if self.coded:
b = self.binary_source([batch_size, self.num_tx, 1, self.k])
c = self.encoder(b)
else:
c = self.binary_source([batch_size, self.num_tx, 1, self.n])
bits_shape = tf.shape(c)
x,x_ind = self.mapper(c)
x_rg = self.rg_mapper(x)
##################################
# Channel
##################################
no = ebnodb2no(ebno_db, self.num_bits_per_symbol, self.coderate, resource_grid=self.rg)
topology = gen_single_sector_topology(batch_size, self.num_tx, 'umi', min_ut_velocity=SPEED, max_ut_velocity=SPEED)
CHANNEL_MODEL.set_topology(*topology)
y_rg, h_freq = self.channel((x_rg, no))
###################################
# Receiver
###################################
# Channel estimation
if self.perf_csi:
h_hat = h_freq
err_var = 0.0
else:
h_hat,err_var = self.channel_estimator((y_rg,no))
# Detection
if self.det_method == "mmse-pic":
if self._output == "bit":
prior_shape = bits_shape
elif self._output == "symbol":
prior_shape = tf.concat([tf.shape(x), [self.num_bits_per_symbol]], axis=0)
prior = tf.zeros(prior_shape)
det_out = self.detector((y_rg,h_hat,prior,err_var,no))
else:
det_out = self.detector((y_rg,h_hat,err_var,no))
# (Decoding) and output
if self._output == "bit":
llr = tf.reshape(det_out, bits_shape)
b_hat = self.decoder(llr)
return b, b_hat
elif self._output == "symbol":
x_hat = tf.reshape(det_out, tf.shape(x_ind))
return x_ind, x_hat
The following function is used to evaluate all of the considered detectors for a given setup: It instantiates the end-to-end systems, runs the simulations, and returns the BER or SER.
[18]:
def run_sim(num_tx, num_bits_per_symbol, output, ebno_dbs, perf_csi, det_param=None):
lmmse = MIMOOFDMLink(output, "lmmse", perf_csi, num_tx, num_bits_per_symbol, det_param)
k_best = MIMOOFDMLink(output, "k-best", perf_csi, num_tx, num_bits_per_symbol, det_param)
ep = MIMOOFDMLink(output, "ep", perf_csi, num_tx, num_bits_per_symbol, det_param)
mmse_pic = MIMOOFDMLink(output, "mmse-pic", perf_csi, num_tx, num_bits_per_symbol, det_param)
if output == "symbol":
soft_estimates = False
ylabel = "Uncoded SER"
else:
soft_estimates = True
ylabel = "Coded BER"
er_lmmse,_ = sim_ber(lmmse,
ebno_dbs,
batch_size=64,
max_mc_iter=200,
num_target_block_errors=200,
soft_estimates=soft_estimates);
er_ep,_ = sim_ber(ep,
ebno_dbs,
batch_size=64,
max_mc_iter=200,
num_target_block_errors=200,
soft_estimates=soft_estimates);
er_kbest,_ = sim_ber(k_best,
ebno_dbs,
batch_size=64,
max_mc_iter=200,
num_target_block_errors=200,
soft_estimates=soft_estimates);
er_mmse_pic,_ = sim_ber(mmse_pic,
ebno_dbs,
batch_size=64,
max_mc_iter=200,
num_target_block_errors=200,
soft_estimates=soft_estimates);
return er_lmmse, er_ep, er_kbest, er_mmse_pic
The next cell defines the simulation parameters.
[19]:
# Range of SNR (dB)
EBN0_DBs = np.linspace(-10., 20.0, 10)
# Number of transmitters
NUM_TX = 4
# Modulation order (number of bits per symbol)
NUM_BITS_PER_SYMBOL = 4 # 16-QAM
We start by evaluating the uncoded SER. The next cell runs the simulations with perfect CSI and channel estimation. Results are stored in the SER dictionary.
[20]:
SER = {} # Store the results
# Perfect CSI
ser_lmmse, ser_ep, ser_kbest, ser_mmse_pic = run_sim(NUM_TX, NUM_BITS_PER_SYMBOL, "symbol", EBN0_DBs, True)
SER['Perf. CSI / LMMSE'] = ser_lmmse
SER['Perf. CSI / EP'] = ser_ep
SER['Perf. CSI / K-Best'] = ser_kbest
SER['Perf. CSI / MMSE-PIC'] = ser_mmse_pic
# Imperfect CSI
ser_lmmse, ser_ep, ser_kbest, ser_mmse_pic = run_sim(NUM_TX, NUM_BITS_PER_SYMBOL, "symbol", EBN0_DBs, False)
SER['Ch. Est. / LMMSE'] = ser_lmmse
SER['Ch. Est. / EP'] = ser_ep
SER['Ch. Est. / K-Best'] = ser_kbest
SER['Ch. Est. / MMSE-PIC'] = ser_mmse_pic
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status
---------------------------------------------------------------------------------------------------------------------------------------
-10.0 | 6.1633e-01 | 1.0000e+00 | 90881 | 147456 | 256 | 256 | 5.5 |reached target block errors
-6.667 | 5.1253e-01 | 1.0000e+00 | 75576 | 147456 | 256 | 256 | 0.1 |reached target block errors
-3.333 | 4.0691e-01 | 9.9609e-01 | 60002 | 147456 | 255 | 256 | 0.1 |reached target block errors
0.0 | 2.5879e-01 | 9.6875e-01 | 38160 | 147456 | 248 | 256 | 0.1 |reached target block errors
3.333 | 1.3966e-01 | 9.2578e-01 | 20593 | 147456 | 237 | 256 | 0.1 |reached target block errors
6.667 | 6.3636e-02 | 7.3242e-01 | 18767 | 294912 | 375 | 512 | 0.2 |reached target block errors
10.0 | 2.1942e-02 | 5.1172e-01 | 6471 | 294912 | 262 | 512 | 0.2 |reached target block errors
13.333 | 9.0287e-03 | 2.7734e-01 | 3994 | 442368 | 213 | 768 | 0.3 |reached target block errors
16.667 | 2.0142e-03 | 1.2054e-01 | 2079 | 1032192 | 216 | 1792 | 0.6 |reached target block errors
20.0 | 4.8549e-04 | 4.7105e-02 | 1217 | 2506752 | 205 | 4352 | 1.4 |reached target block errors
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status
---------------------------------------------------------------------------------------------------------------------------------------
-10.0 | 6.1664e-01 | 1.0000e+00 | 90927 | 147456 | 256 | 256 | 5.8 |reached target block errors
-6.667 | 4.8715e-01 | 1.0000e+00 | 71833 | 147456 | 256 | 256 | 0.1 |reached target block errors
-3.333 | 3.2039e-01 | 9.8828e-01 | 47244 | 147456 | 253 | 256 | 0.1 |reached target block errors
0.0 | 1.6007e-01 | 9.7656e-01 | 23604 | 147456 | 250 | 256 | 0.1 |reached target block errors
3.333 | 4.0738e-02 | 8.0859e-01 | 6007 | 147456 | 207 | 256 | 0.1 |reached target block errors
6.667 | 1.0342e-02 | 4.4336e-01 | 3050 | 294912 | 227 | 512 | 0.2 |reached target block errors
10.0 | 1.9165e-03 | 1.6172e-01 | 1413 | 737280 | 207 | 1280 | 0.5 |reached target block errors
13.333 | 2.7252e-04 | 2.9225e-02 | 1085 | 3981312 | 202 | 6912 | 2.7 |reached target block errors
16.667 | 5.8245e-05 | 4.4866e-03 | 1503 | 25804800 | 201 | 44800 | 17.4 |reached target block errors
20.0 | 4.2725e-06 | 6.4453e-04 | 126 | 29491200 | 33 | 51200 | 19.7 |reached max iter
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status
---------------------------------------------------------------------------------------------------------------------------------------
-10.0 | 6.5043e-01 | 1.0000e+00 | 95910 | 147456 | 256 | 256 | 5.6 |reached target block errors
-6.667 | 4.8913e-01 | 1.0000e+00 | 72125 | 147456 | 256 | 256 | 0.5 |reached target block errors
-3.333 | 3.1826e-01 | 1.0000e+00 | 46929 | 147456 | 256 | 256 | 0.6 |reached target block errors
0.0 | 1.2128e-01 | 9.6094e-01 | 17883 | 147456 | 246 | 256 | 0.6 |reached target block errors
3.333 | 3.9100e-02 | 7.5000e-01 | 11531 | 294912 | 384 | 512 | 1.1 |reached target block errors
6.667 | 7.3310e-03 | 2.8906e-01 | 3243 | 442368 | 222 | 768 | 1.6 |reached target block errors
10.0 | 1.0640e-03 | 8.0859e-02 | 1569 | 1474560 | 207 | 2560 | 5.6 |reached target block errors
13.333 | 1.9466e-04 | 1.4757e-02 | 1550 | 7962624 | 204 | 13824 | 30.0 |reached target block errors
16.667 | 4.4522e-05 | 2.3437e-03 | 1313 | 29491200 | 120 | 51200 | 110.7 |reached max iter
20.0 | 9.4265e-06 | 5.6641e-04 | 278 | 29491200 | 29 | 51200 | 111.2 |reached max iter
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status
---------------------------------------------------------------------------------------------------------------------------------------
-10.0 | 6.1027e-01 | 1.0000e+00 | 89988 | 147456 | 256 | 256 | 5.7 |reached target block errors
-6.667 | 4.8936e-01 | 1.0000e+00 | 72159 | 147456 | 256 | 256 | 0.1 |reached target block errors
-3.333 | 2.9184e-01 | 9.9609e-01 | 43033 | 147456 | 255 | 256 | 0.1 |reached target block errors
0.0 | 1.7076e-01 | 9.6875e-01 | 25179 | 147456 | 248 | 256 | 0.1 |reached target block errors
3.333 | 6.4514e-02 | 8.9844e-01 | 9513 | 147456 | 230 | 256 | 0.1 |reached target block errors
6.667 | 1.3234e-02 | 6.1914e-01 | 3903 | 294912 | 317 | 512 | 0.2 |reached target block errors
10.0 | 3.1687e-03 | 2.5684e-01 | 1869 | 589824 | 263 | 1024 | 0.4 |reached target block errors
13.333 | 5.5892e-04 | 6.6732e-02 | 989 | 1769472 | 205 | 3072 | 1.3 |reached target block errors
16.667 | 7.5696e-05 | 1.1489e-02 | 759 | 10027008 | 200 | 17408 | 7.2 |reached target block errors
20.0 | 8.2737e-06 | 1.4062e-03 | 244 | 29491200 | 72 | 51200 | 20.9 |reached max iter
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status
---------------------------------------------------------------------------------------------------------------------------------------
-10.0 | 6.7265e-01 | 1.0000e+00 | 99187 | 147456 | 256 | 256 | 4.7 |reached target block errors
-6.667 | 5.5809e-01 | 1.0000e+00 | 82294 | 147456 | 256 | 256 | 0.3 |reached target block errors
-3.333 | 4.2839e-01 | 1.0000e+00 | 63169 | 147456 | 256 | 256 | 0.3 |reached target block errors
0.0 | 3.1073e-01 | 1.0000e+00 | 45819 | 147456 | 256 | 256 | 0.2 |reached target block errors
3.333 | 1.7369e-01 | 9.5703e-01 | 25611 | 147456 | 245 | 256 | 0.2 |reached target block errors
6.667 | 8.6216e-02 | 8.3594e-01 | 12713 | 147456 | 214 | 256 | 0.3 |reached target block errors
10.0 | 5.5674e-02 | 6.7969e-01 | 16419 | 294912 | 348 | 512 | 0.5 |reached target block errors
13.333 | 1.4971e-02 | 4.5898e-01 | 4415 | 294912 | 235 | 512 | 0.5 |reached target block errors
16.667 | 8.6772e-03 | 2.3535e-01 | 5118 | 589824 | 241 | 1024 | 1.0 |reached target block errors
20.0 | 4.2171e-03 | 1.3281e-01 | 3731 | 884736 | 204 | 1536 | 1.6 |reached target block errors
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status
---------------------------------------------------------------------------------------------------------------------------------------
-10.0 | 6.6232e-01 | 1.0000e+00 | 97663 | 147456 | 256 | 256 | 5.5 |reached target block errors
-6.667 | 5.3370e-01 | 1.0000e+00 | 78698 | 147456 | 256 | 256 | 0.3 |reached target block errors
-3.333 | 3.9173e-01 | 1.0000e+00 | 57763 | 147456 | 256 | 256 | 0.3 |reached target block errors
0.0 | 2.2822e-01 | 9.8438e-01 | 33653 | 147456 | 252 | 256 | 0.3 |reached target block errors
3.333 | 8.1868e-02 | 9.1406e-01 | 12072 | 147456 | 234 | 256 | 0.3 |reached target block errors
6.667 | 2.5923e-02 | 6.8359e-01 | 7645 | 294912 | 350 | 512 | 0.6 |reached target block errors
10.0 | 1.1207e-02 | 4.3164e-01 | 3305 | 294912 | 221 | 512 | 0.6 |reached target block errors
13.333 | 1.9967e-03 | 1.3616e-01 | 2061 | 1032192 | 244 | 1792 | 1.9 |reached target block errors
16.667 | 1.0882e-03 | 6.2800e-02 | 2086 | 1916928 | 209 | 3328 | 3.5 |reached target block errors
20.0 | 1.1692e-03 | 5.6771e-02 | 2586 | 2211840 | 218 | 3840 | 4.1 |reached target block errors
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status
---------------------------------------------------------------------------------------------------------------------------------------
-10.0 | 6.8175e-01 | 1.0000e+00 | 100528 | 147456 | 256 | 256 | 7.2 |reached target block errors
-6.667 | 5.4227e-01 | 1.0000e+00 | 79961 | 147456 | 256 | 256 | 0.8 |reached target block errors
-3.333 | 3.4616e-01 | 1.0000e+00 | 51044 | 147456 | 256 | 256 | 0.7 |reached target block errors
0.0 | 1.9120e-01 | 9.8438e-01 | 28194 | 147456 | 252 | 256 | 0.7 |reached target block errors
3.333 | 6.7600e-02 | 8.7109e-01 | 9968 | 147456 | 223 | 256 | 0.7 |reached target block errors
6.667 | 2.2244e-02 | 6.3281e-01 | 6560 | 294912 | 324 | 512 | 1.5 |reached target block errors
10.0 | 6.9128e-03 | 2.9688e-01 | 3058 | 442368 | 228 | 768 | 2.2 |reached target block errors
13.333 | 2.8677e-03 | 1.1384e-01 | 2960 | 1032192 | 204 | 1792 | 5.1 |reached target block errors
16.667 | 1.1091e-03 | 6.1298e-02 | 2126 | 1916928 | 204 | 3328 | 9.6 |reached target block errors
20.0 | 5.6476e-04 | 4.3403e-02 | 1499 | 2654208 | 200 | 4608 | 13.2 |reached target block errors
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status
---------------------------------------------------------------------------------------------------------------------------------------
-10.0 | 6.5792e-01 | 1.0000e+00 | 97014 | 147456 | 256 | 256 | 5.3 |reached target block errors
-6.667 | 5.3354e-01 | 1.0000e+00 | 78674 | 147456 | 256 | 256 | 0.3 |reached target block errors
-3.333 | 3.7783e-01 | 1.0000e+00 | 55714 | 147456 | 256 | 256 | 0.3 |reached target block errors
0.0 | 2.3106e-01 | 9.8438e-01 | 34071 | 147456 | 252 | 256 | 0.3 |reached target block errors
3.333 | 9.3486e-02 | 9.0625e-01 | 13785 | 147456 | 232 | 256 | 0.3 |reached target block errors
6.667 | 2.5380e-02 | 7.4414e-01 | 7485 | 294912 | 381 | 512 | 0.6 |reached target block errors
10.0 | 7.6090e-03 | 4.1211e-01 | 2244 | 294912 | 211 | 512 | 0.6 |reached target block errors
13.333 | 2.4804e-03 | 2.1289e-01 | 1463 | 589824 | 218 | 1024 | 1.1 |reached target block errors
16.667 | 8.9970e-04 | 9.8524e-02 | 1194 | 1327104 | 227 | 2304 | 2.5 |reached target block errors
20.0 | 2.8517e-03 | 5.7199e-02 | 5887 | 2064384 | 205 | 3584 | 4.0 |reached target block errors
Next, we evaluate the coded BER. The cell below runs the simulations with perfect CSI and channel estimation. Results are stored in the BER dictionary.
[21]:
BER = {} # Store the results
# Perfect CSI
ber_lmmse, ber_ep, ber_kbest, ber_mmse_pic = run_sim(NUM_TX, NUM_BITS_PER_SYMBOL, "bit", EBN0_DBs, True)
BER['Perf. CSI / LMMSE'] = ber_lmmse
BER['Perf. CSI / EP'] = ber_ep
BER['Perf. CSI / K-Best'] = ber_kbest
BER['Perf. CSI / MMSE-PIC'] = ber_mmse_pic
# Imperfect CSI
ber_lmmse, ber_ep, ber_kbest, ber_mmse_pic = run_sim(NUM_TX, NUM_BITS_PER_SYMBOL, "bit", EBN0_DBs, False)
BER['Ch. Est. / LMMSE'] = ber_lmmse
BER['Ch. Est. / EP'] = ber_ep
BER['Ch. Est. / K-Best'] = ber_kbest
BER['Ch. Est. / MMSE-PIC'] = ber_mmse_pic
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status
---------------------------------------------------------------------------------------------------------------------------------------
-10.0 | 1.8752e-01 | 8.4766e-01 | 55302 | 294912 | 217 | 256 | 8.2 |reached target block errors
-6.667 | 1.0936e-01 | 5.8008e-01 | 64501 | 589824 | 297 | 512 | 0.2 |reached target block errors
-3.333 | 5.8125e-02 | 3.3594e-01 | 51425 | 884736 | 258 | 768 | 0.4 |reached target block errors
0.0 | 2.0881e-02 | 1.3802e-01 | 36948 | 1769472 | 212 | 1536 | 0.7 |reached target block errors
3.333 | 7.0182e-03 | 5.0049e-02 | 33116 | 4718592 | 205 | 4096 | 1.9 |reached target block errors
6.667 | 1.7441e-03 | 1.1837e-02 | 33948 | 19464192 | 200 | 16896 | 7.8 |reached target block errors
10.0 | 3.2945e-04 | 2.5781e-03 | 19432 | 58982400 | 132 | 51200 | 23.6 |reached max iter
13.333 | 4.9608e-05 | 4.2969e-04 | 2926 | 58982400 | 22 | 51200 | 23.5 |reached max iter
16.667 | 0.0000e+00 | 0.0000e+00 | 0 | 58982400 | 0 | 51200 | 23.6 |reached max iter
Simulation stopped as no error occurred @ EbNo = 16.7 dB.
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status
---------------------------------------------------------------------------------------------------------------------------------------
-10.0 | 1.7784e-01 | 8.1641e-01 | 52448 | 294912 | 209 | 256 | 6.1 |reached target block errors
-6.667 | 1.0072e-01 | 5.5078e-01 | 59409 | 589824 | 282 | 512 | 0.3 |reached target block errors
-3.333 | 3.7651e-02 | 2.4316e-01 | 44415 | 1179648 | 249 | 1024 | 0.6 |reached target block errors
0.0 | 7.0220e-03 | 4.9072e-02 | 33134 | 4718592 | 201 | 4096 | 2.2 |reached target block errors
3.333 | 8.8641e-04 | 6.8873e-03 | 29801 | 33619968 | 201 | 29184 | 15.5 |reached target block errors
6.667 | 1.0232e-04 | 8.7891e-04 | 6035 | 58982400 | 45 | 51200 | 27.1 |reached max iter
10.0 | 1.1512e-05 | 1.5625e-04 | 679 | 58982400 | 8 | 51200 | 27.1 |reached max iter
13.333 | 0.0000e+00 | 0.0000e+00 | 0 | 58982400 | 0 | 51200 | 27.1 |reached max iter
Simulation stopped as no error occurred @ EbNo = 13.3 dB.
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status
---------------------------------------------------------------------------------------------------------------------------------------
-10.0 | 2.0344e-01 | 9.1797e-01 | 59997 | 294912 | 235 | 256 | 6.4 |reached target block errors
-6.667 | 1.2116e-01 | 6.8945e-01 | 71466 | 589824 | 353 | 512 | 1.3 |reached target block errors
-3.333 | 3.3782e-02 | 2.2070e-01 | 39851 | 1179648 | 226 | 1024 | 2.6 |reached target block errors
0.0 | 5.5129e-03 | 3.7574e-02 | 34142 | 6193152 | 202 | 5376 | 13.8 |reached target block errors
3.333 | 6.2818e-04 | 4.8169e-03 | 30197 | 48070656 | 201 | 41728 | 107.0 |reached target block errors
6.667 | 9.2451e-05 | 6.4453e-04 | 5453 | 58982400 | 33 | 51200 | 131.4 |reached max iter
10.0 | 6.6969e-06 | 9.7656e-05 | 395 | 58982400 | 5 | 51200 | 131.4 |reached max iter
13.333 | 0.0000e+00 | 0.0000e+00 | 0 | 58982400 | 0 | 51200 | 131.4 |reached max iter
Simulation stopped as no error occurred @ EbNo = 13.3 dB.
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status
---------------------------------------------------------------------------------------------------------------------------------------
-10.0 | 1.8316e-01 | 8.5938e-01 | 54015 | 294912 | 220 | 256 | 5.1 |reached target block errors
-6.667 | 1.2096e-01 | 6.4062e-01 | 71346 | 589824 | 328 | 512 | 0.3 |reached target block errors
-3.333 | 4.9321e-02 | 3.0599e-01 | 43636 | 884736 | 235 | 768 | 0.4 |reached target block errors
0.0 | 1.2342e-02 | 9.0278e-02 | 32758 | 2654208 | 208 | 2304 | 1.3 |reached target block errors
3.333 | 1.4455e-03 | 1.4560e-02 | 23447 | 16220160 | 205 | 14080 | 7.6 |reached target block errors
6.667 | 1.3017e-04 | 1.6992e-03 | 7678 | 58982400 | 87 | 51200 | 27.5 |reached max iter
10.0 | 1.8531e-05 | 1.9531e-04 | 1093 | 58982400 | 10 | 51200 | 27.4 |reached max iter
13.333 | 0.0000e+00 | 0.0000e+00 | 0 | 58982400 | 0 | 51200 | 27.3 |reached max iter
Simulation stopped as no error occurred @ EbNo = 13.3 dB.
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status
---------------------------------------------------------------------------------------------------------------------------------------
-10.0 | 2.1603e-01 | 9.1016e-01 | 63711 | 294912 | 233 | 256 | 7.0 |reached target block errors
-6.667 | 1.3184e-01 | 6.8164e-01 | 77763 | 589824 | 349 | 512 | 0.6 |reached target block errors
-3.333 | 7.8196e-02 | 4.3945e-01 | 46122 | 589824 | 225 | 512 | 0.6 |reached target block errors
0.0 | 3.5376e-02 | 2.2754e-01 | 41731 | 1179648 | 233 | 1024 | 1.2 |reached target block errors
3.333 | 1.2590e-02 | 8.0859e-02 | 37128 | 2949120 | 207 | 2560 | 2.9 |reached target block errors
6.667 | 5.3650e-03 | 3.2878e-02 | 37973 | 7077888 | 202 | 6144 | 7.0 |reached target block errors
10.0 | 1.3640e-03 | 8.8220e-03 | 35801 | 26247168 | 201 | 22784 | 26.2 |reached target block errors
13.333 | 6.3398e-04 | 4.2230e-03 | 34589 | 54558720 | 200 | 47360 | 54.3 |reached target block errors
16.667 | 2.8853e-04 | 2.1289e-03 | 17018 | 58982400 | 109 | 51200 | 58.6 |reached max iter
20.0 | 2.3634e-04 | 1.6016e-03 | 13940 | 58982400 | 82 | 51200 | 58.4 |reached max iter
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status
---------------------------------------------------------------------------------------------------------------------------------------
-10.0 | 2.0562e-01 | 8.7891e-01 | 60639 | 294912 | 225 | 256 | 6.6 |reached target block errors
-6.667 | 1.3133e-01 | 6.6602e-01 | 77459 | 589824 | 341 | 512 | 0.6 |reached target block errors
-3.333 | 6.3354e-02 | 3.7109e-01 | 56052 | 884736 | 285 | 768 | 0.9 |reached target block errors
0.0 | 2.2274e-02 | 1.3997e-01 | 39414 | 1769472 | 215 | 1536 | 1.9 |reached target block errors
3.333 | 4.8379e-03 | 3.1250e-02 | 35669 | 7372800 | 200 | 6400 | 7.8 |reached target block errors
6.667 | 1.0846e-03 | 8.5343e-03 | 29426 | 27131904 | 201 | 23552 | 28.7 |reached target block errors
10.0 | 5.2161e-04 | 3.8867e-03 | 30766 | 58982400 | 199 | 51200 | 62.4 |reached max iter
13.333 | 2.8222e-04 | 2.4219e-03 | 16646 | 58982400 | 124 | 51200 | 62.3 |reached max iter
16.667 | 1.4404e-04 | 1.4453e-03 | 8496 | 58982400 | 74 | 51200 | 61.1 |reached max iter
20.0 | 1.6247e-04 | 1.3281e-03 | 9583 | 58982400 | 68 | 51200 | 58.5 |reached max iter
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status
---------------------------------------------------------------------------------------------------------------------------------------
-10.0 | 2.3040e-01 | 9.4531e-01 | 67948 | 294912 | 242 | 256 | 7.2 |reached target block errors
-6.667 | 1.4620e-01 | 7.3633e-01 | 86235 | 589824 | 377 | 512 | 1.6 |reached target block errors
-3.333 | 6.7522e-02 | 3.9844e-01 | 59739 | 884736 | 306 | 768 | 2.4 |reached target block errors
0.0 | 1.6000e-02 | 1.0107e-01 | 37748 | 2359296 | 207 | 2048 | 6.4 |reached target block errors
3.333 | 3.4144e-03 | 2.0117e-02 | 40278 | 11796480 | 206 | 10240 | 31.8 |reached target block errors
6.667 | 1.0244e-03 | 6.2314e-03 | 38065 | 37158912 | 201 | 32256 | 100.2 |reached target block errors
10.0 | 4.0466e-04 | 3.0469e-03 | 23868 | 58982400 | 156 | 51200 | 158.7 |reached max iter
13.333 | 1.8073e-04 | 1.7383e-03 | 10660 | 58982400 | 89 | 51200 | 158.8 |reached max iter
16.667 | 2.2430e-04 | 1.5625e-03 | 13230 | 58982400 | 80 | 51200 | 158.7 |reached max iter
20.0 | 1.1420e-04 | 9.5703e-04 | 6736 | 58982400 | 49 | 51200 | 158.7 |reached max iter
EbNo [dB] | BER | BLER | bit errors | num bits | block errors | num blocks | runtime [s] | status
---------------------------------------------------------------------------------------------------------------------------------------
-10.0 | 2.2212e-01 | 9.1406e-01 | 65507 | 294912 | 234 | 256 | 5.6 |reached target block errors
-6.667 | 1.4437e-01 | 7.2070e-01 | 85150 | 589824 | 369 | 512 | 0.6 |reached target block errors
-3.333 | 7.1927e-02 | 4.0820e-01 | 42424 | 589824 | 209 | 512 | 0.6 |reached target block errors
0.0 | 2.7839e-02 | 1.7813e-01 | 41050 | 1474560 | 228 | 1280 | 1.5 |reached target block errors
3.333 | 6.0441e-03 | 5.2604e-02 | 26737 | 4423680 | 202 | 3840 | 4.4 |reached target block errors
6.667 | 1.4097e-03 | 1.3374e-02 | 24529 | 17399808 | 202 | 15104 | 17.5 |reached target block errors
10.0 | 5.1038e-04 | 5.4633e-03 | 21524 | 42172416 | 200 | 36608 | 42.3 |reached target block errors
13.333 | 3.9658e-04 | 2.8320e-03 | 23391 | 58982400 | 145 | 51200 | 59.2 |reached max iter
16.667 | 2.6315e-04 | 2.2461e-03 | 15521 | 58982400 | 115 | 51200 | 59.2 |reached max iter
20.0 | 2.0064e-04 | 1.8945e-03 | 11834 | 58982400 | 97 | 51200 | 59.2 |reached max iter
Finally, we plot the results.
[22]:
fig, ax = plt.subplots(1,2, figsize=(16,7))
fig.suptitle(f"{NUM_TX}x{NUM_RX_ANT} UMi | {2**NUM_BITS_PER_SYMBOL}-QAM")
## SER
ax[0].set_title("Symbol error rate")
# Perfect CSI
ax[0].semilogy(EBN0_DBs, SER['Perf. CSI / LMMSE'], 'x-', label='Perf. CSI / LMMSE', c='C0')
ax[0].semilogy(EBN0_DBs, SER['Perf. CSI / EP'], 'o--', label='Perf. CSI / EP', c='C0')
ax[0].semilogy(EBN0_DBs, SER['Perf. CSI / K-Best'], 's-.', label='Perf. CSI / K-Best', c='C0')
ax[0].semilogy(EBN0_DBs, SER['Perf. CSI / MMSE-PIC'], 'd:', label='Perf. CSI / MMSE-PIC', c='C0')
# Imperfect CSI
ax[0].semilogy(EBN0_DBs, SER['Ch. Est. / LMMSE'], 'x-', label='Ch. Est. / LMMSE', c='C1')
ax[0].semilogy(EBN0_DBs, SER['Ch. Est. / EP'], 'o--', label='Ch. Est. / EP', c='C1')
ax[0].semilogy(EBN0_DBs, SER['Ch. Est. / K-Best'], 's-.', label='Ch. Est. / K-Best', c='C1')
ax[0].semilogy(EBN0_DBs, SER['Ch. Est. / MMSE-PIC'], 'd:', label='Ch. Est. / MMSE-PIC', c='C1')
ax[0].set_xlabel(r"$E_b/N0$")
ax[0].set_ylabel("SER")
ax[0].set_ylim((1e-4, 1.0))
ax[0].legend()
ax[0].grid(True)
## SER
ax[1].set_title("Bit error rate")
# Perfect CSI
ax[1].semilogy(EBN0_DBs, BER['Perf. CSI / LMMSE'], 'x-', label='Perf. CSI / LMMSE', c='C0')
ax[1].semilogy(EBN0_DBs, BER['Perf. CSI / EP'], 'o--', label='Perf. CSI / EP', c='C0')
ax[1].semilogy(EBN0_DBs, BER['Perf. CSI / K-Best'], 's-.', label='Perf. CSI / K-Best', c='C0')
ax[1].semilogy(EBN0_DBs, BER['Perf. CSI / MMSE-PIC'], 'd:', label='Perf. CSI / MMSE-PIC', c='C0')
# Imperfect CSI
ax[1].semilogy(EBN0_DBs, BER['Ch. Est. / LMMSE'], 'x-', label='Ch. Est. / LMMSE', c='C1')
ax[1].semilogy(EBN0_DBs, BER['Ch. Est. / EP'], 'o--', label='Ch. Est. / EP', c='C1')
ax[1].semilogy(EBN0_DBs, BER['Ch. Est. / K-Best'], 's-.', label='Ch. Est. / K-Best', c='C1')
ax[1].semilogy(EBN0_DBs, BER['Ch. Est. / MMSE-PIC'], 'd:', label='Ch. Est. / MMSE-PIC', c='C1')
ax[1].set_xlabel(r"$E_b/N0$")
ax[1].set_ylabel("BER")
ax[1].set_ylim((1e-4, 1.0))
ax[1].legend()
ax[1].grid(True)
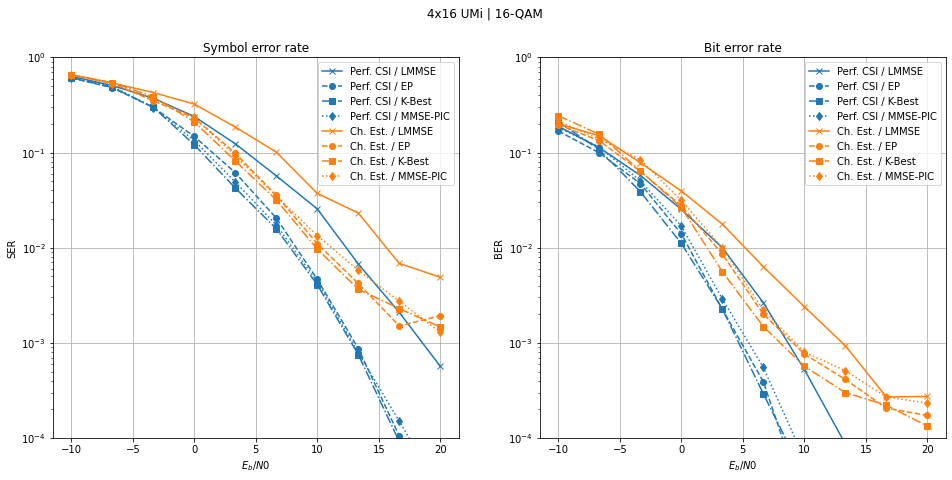
For this setup, the non-linear detection algorithms K-Best, EP, and MMSE-PIC, outperform the linear MMSE detection method. It is remarkable that K-Best and EP with imperfect CSI achieve lower BER than LMMSE detection with perfect CSI.
However, one should keep in mind that:
EP is prone to numerical imprecision and could therefore achieve better BER/SER with double precision (
dtype=tf.complex128). The number of iterationslas well as the update smoothing parameterbetaimpact performance.For K-Best, there is not a unique way to compute soft information and better performance could be achieved with improved methods for computing soft information from a list of candidates (see list2llr). Increasing the list size
kresults in improved accuracy at the cost of higher complexity.MMSE-PIC can be easily combined with a decoder to implement iterative detection and decoding, as it takes as input soft prior information on the bits/symbols.