Discrete
This module provides layers and functions that implement channel models with discrete input/output alphabets.
All channel models support binary inputs \(x \in \{0, 1\}\) and bipolar inputs \(x \in \{-1, 1\}\), respectively. In the later case, it is assumed that each 0 is mapped to -1.
The channels can either return discrete values or log-likelihood ratios (LLRs). These LLRs describe the channel transition probabilities \(L(y|X=1)=L(X=1|y)+L_a(X=1)\) where \(L_a(X=1)=\operatorname{log} \frac{P(X=1)}{P(X=0)}\) depends only on the a priori probability of \(X=1\). These LLRs equal the a posteriori probability if \(P(X=1)=P(X=0)=0.5\).
Further, the channel reliability parameter \(p_b\) can be either a scalar value or a tensor of any shape that can be broadcasted to the input. This allows for the efficient implementation of channels with non-uniform error probabilities.
The channel models are based on the Gumble-softmax trick [GumbleSoftmax] to ensure differentiability of the channel w.r.t. to the channel reliability parameter. Please see [LearningShaping] for further details.
Setting-up:
>>> bsc = BinarySymmetricChannel(return_llrs=False, bipolar_input=False)
Running:
>>> x = tf.zeros((128,)) # x is the channel input
>>> pb = 0.1 # pb is the bit flipping probability
>>> y = bsc((x, pb))
BinaryMemorylessChannel
- class sionna.channel.BinaryMemorylessChannel(return_llrs=False, bipolar_input=False, llr_max=100., dtype=tf.float32, **kwargs)[source]
Discrete binary memory less channel with (possibly) asymmetric bit flipping probabilities.
Inputs bits are flipped with probability \(p_\text{b,0}\) and \(p_\text{b,1}\), respectively.
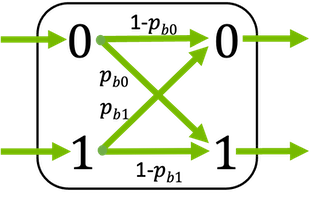
This layer supports binary inputs (\(x \in \{0, 1\}\)) and bipolar inputs (\(x \in \{-1, 1\}\)).
If activated, the channel directly returns log-likelihood ratios (LLRs) defined as
\[\begin{split}\ell = \begin{cases} \operatorname{log} \frac{p_{b,1}}{1-p_{b,0}}, \qquad \text{if} \, y=0 \\ \operatorname{log} \frac{1-p_{b,1}}{p_{b,0}}, \qquad \text{if} \, y=1 \\ \end{cases}\end{split}\]The error probability \(p_\text{b}\) can be either scalar or a tensor (broadcastable to the shape of the input). This allows different erasure probabilities per bit position. In any case, its last dimension must be of length 2 and is interpreted as \(p_\text{b,0}\) and \(p_\text{b,1}\).
This class inherits from the Keras Layer class and can be used as layer in a Keras model.
- Parameters:
return_llrs (bool) – Defaults to False. If True, the layer returns log-likelihood ratios instead of binary values based on
pb.bipolar_input (bool, False) – Defaults to False. If True, the expected input is given as \(\{-1,1\}\) instead of \(\{0,1\}\).
llr_max (tf.float) – Defaults to 100. Defines the clipping value of the LLRs.
dtype (tf.DType) – Defines the datatype for internal calculations and the output dtype. Defaults to tf.float32.
- Input:
(x, pb) – Tuple:
x ([…,n], tf.float32) – Input sequence to the channel consisting of binary values \(\{0,1\} ` or :math:\){-1,1}`, respectively.
pb ([…,2], tf.float32) – Error probability. Can be a tuple of two scalars or of any shape that can be broadcasted to the shape of
x. It has an additional last dimension which is interpreted as \(p_\text{b,0}\) and \(p_\text{b,1}\).
- Output:
[…,n], tf.float32 – Output sequence of same length as the input
x. Ifreturn_llrsis False, the output is ternary where a -1 and 0 indicate an erasure for the binary and bipolar input, respectively.
- property llr_max
Maximum value used for LLR calculations.
- property temperature
Temperature for Gumble-softmax trick.
BinarySymmetricChannel
- class sionna.channel.BinarySymmetricChannel(return_llrs=False, bipolar_input=False, llr_max=100., dtype=tf.float32, **kwargs)[source]
Discrete binary symmetric channel which randomly flips bits with probability \(p_\text{b}\).
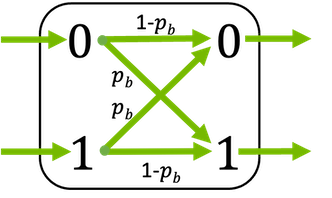
This layer supports binary inputs (\(x \in \{0, 1\}\)) and bipolar inputs (\(x \in \{-1, 1\}\)).
If activated, the channel directly returns log-likelihood ratios (LLRs) defined as
\[\begin{split}\ell = \begin{cases} \operatorname{log} \frac{p_{b}}{1-p_{b}}, \qquad \text{if}\, y=0 \\ \operatorname{log} \frac{1-p_{b}}{p_{b}}, \qquad \text{if}\, y=1 \\ \end{cases}\end{split}\]where \(y\) denotes the binary output of the channel.
The bit flipping probability \(p_\text{b}\) can be either a scalar or a tensor (broadcastable to the shape of the input). This allows different bit flipping probabilities per bit position.
This class inherits from the Keras Layer class and can be used as layer in a Keras model.
- Parameters:
return_llrs (bool) – Defaults to False. If True, the layer returns log-likelihood ratios instead of binary values based on
pb.bipolar_input (bool, False) – Defaults to False. If True, the expected input is given as {-1,1} instead of {0,1}.
llr_max (tf.float) – Defaults to 100. Defines the clipping value of the LLRs.
dtype (tf.DType) – Defines the datatype for internal calculations and the output dtype. Defaults to tf.float32.
- Input:
(x, pb) – Tuple:
x ([…,n], tf.float32) – Input sequence to the channel.
pb (tf.float32) – Bit flipping probability. Can be a scalar or of any shape that can be broadcasted to the shape of
x.
- Output:
[…,n], tf.float32 – Output sequence of same length as the input
x. Ifreturn_llrsis False, the output is binary and otherwise soft-values are returned.
BinaryErasureChannel
- class sionna.channel.BinaryErasureChannel(return_llrs=False, bipolar_input=False, llr_max=100., dtype=tf.float32, **kwargs)[source]
Binary erasure channel (BEC) where a bit is either correctly received or erased.
In the binary erasure channel, bits are always correctly received or erased with erasure probability \(p_\text{b}\).
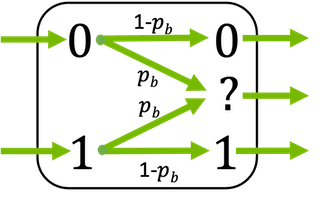
This layer supports binary inputs (\(x \in \{0, 1\}\)) and bipolar inputs (\(x \in \{-1, 1\}\)).
If activated, the channel directly returns log-likelihood ratios (LLRs) defined as
\[\begin{split}\ell = \begin{cases} -\infty, \qquad \text{if} \, y=0 \\ 0, \qquad \quad \,\, \text{if} \, y=? \\ \infty, \qquad \quad \text{if} \, y=1 \\ \end{cases}\end{split}\]The erasure probability \(p_\text{b}\) can be either a scalar or a tensor (broadcastable to the shape of the input). This allows different erasure probabilities per bit position.
Please note that the output of the BEC is ternary. Hereby, -1 indicates an erasure for the binary configuration and 0 for the bipolar mode, respectively.
This class inherits from the Keras Layer class and can be used as layer in a Keras model.
- Parameters:
return_llrs (bool) – Defaults to False. If True, the layer returns log-likelihood ratios instead of binary values based on
pb.bipolar_input (bool, False) – Defaults to False. If True, the expected input is given as {-1,1} instead of {0,1}.
llr_max (tf.float) – Defaults to 100. Defines the clipping value of the LLRs.
dtype (tf.DType) – Defines the datatype for internal calculations and the output dtype. Defaults to tf.float32.
- Input:
(x, pb) – Tuple:
x ([…,n], tf.float32) – Input sequence to the channel.
pb (tf.float32) – Erasure probability. Can be a scalar or of any shape that can be broadcasted to the shape of
x.
- Output:
[…,n], tf.float32 – Output sequence of same length as the input
x. Ifreturn_llrsis False, the output is ternary where each -1 and each 0 indicate an erasure for the binary and bipolar input, respectively.
BinaryZChannel
- class sionna.channel.BinaryZChannel(return_llrs=False, bipolar_input=False, llr_max=100., dtype=tf.float32, **kwargs)[source]
Layer that implements the binary Z-channel.
In the Z-channel, transmission errors only occur for the transmission of second input element (i.e., if a 1 is transmitted) with error probability probability \(p_\text{b}\) but the first element is always correctly received.
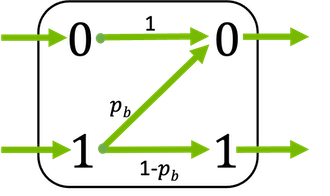
This layer supports binary inputs (\(x \in \{0, 1\}\)) and bipolar inputs (\(x \in \{-1, 1\}\)).
If activated, the channel directly returns log-likelihood ratios (LLRs) defined as
\[\begin{split}\ell = \begin{cases} \operatorname{log} \left( p_b \right), \qquad \text{if} \, y=0 \\ \infty, \qquad \qquad \text{if} \, y=1 \\ \end{cases}\end{split}\]assuming equal probable inputs \(P(X=0) = P(X=1) = 0.5\).
The error probability \(p_\text{b}\) can be either a scalar or a tensor (broadcastable to the shape of the input). This allows different error probabilities per bit position.
This class inherits from the Keras Layer class and can be used as layer in a Keras model.
- Parameters:
return_llrs (bool) – Defaults to False. If True, the layer returns log-likelihood ratios instead of binary values based on
pb.bipolar_input (bool, False) – Defaults to False. If True, the expected input is given as {-1,1} instead of {0,1}.
llr_max (tf.float) – Defaults to 100. Defines the clipping value of the LLRs.
dtype (tf.DType) – Defines the datatype for internal calculations and the output dtype. Defaults to tf.float32.
- Input:
(x, pb) – Tuple:
x ([…,n], tf.float32) – Input sequence to the channel.
pb (tf.float32) – Error probability. Can be a scalar or of any shape that can be broadcasted to the shape of
x.
- Output:
[…,n], tf.float32 – Output sequence of same length as the input
x. Ifreturn_llrsis False, the output is binary and otherwise soft-values are returned.
- References:
- [GumbleSoftmax]
E. Jang, G. Shixiang, and B. Poole. “Categorical reparameterization with gumbel-softmax,” arXiv preprint arXiv:1611.01144 (2016).
[LearningShaping]M. Stark, F. Ait Aoudia, and J. Hoydis. “Joint learning of geometric and probabilistic constellation shaping,” 2019 IEEE Globecom Workshops (GC Wkshps). IEEE, 2019.