Wireless
This module provides layers and functions that implement wireless channel models.
Models currently available include AWGN, flat-fading with (optional) SpatialCorrelation, RayleighBlockFading, as well as models from the 3rd Generation Partnership Project (3GPP) [TR38901]: TDL, CDL, UMi, UMa, and RMa. It is also possible to use externally generated CIRs.
Apart from flat-fading, all of these models generate channel impulse responses (CIRs) that can then be used to implement a channel transfer function in the time domain or assuming an OFDM waveform.
This is achieved using the different functions, classes, and Keras layers which operate as shown in the figures below.
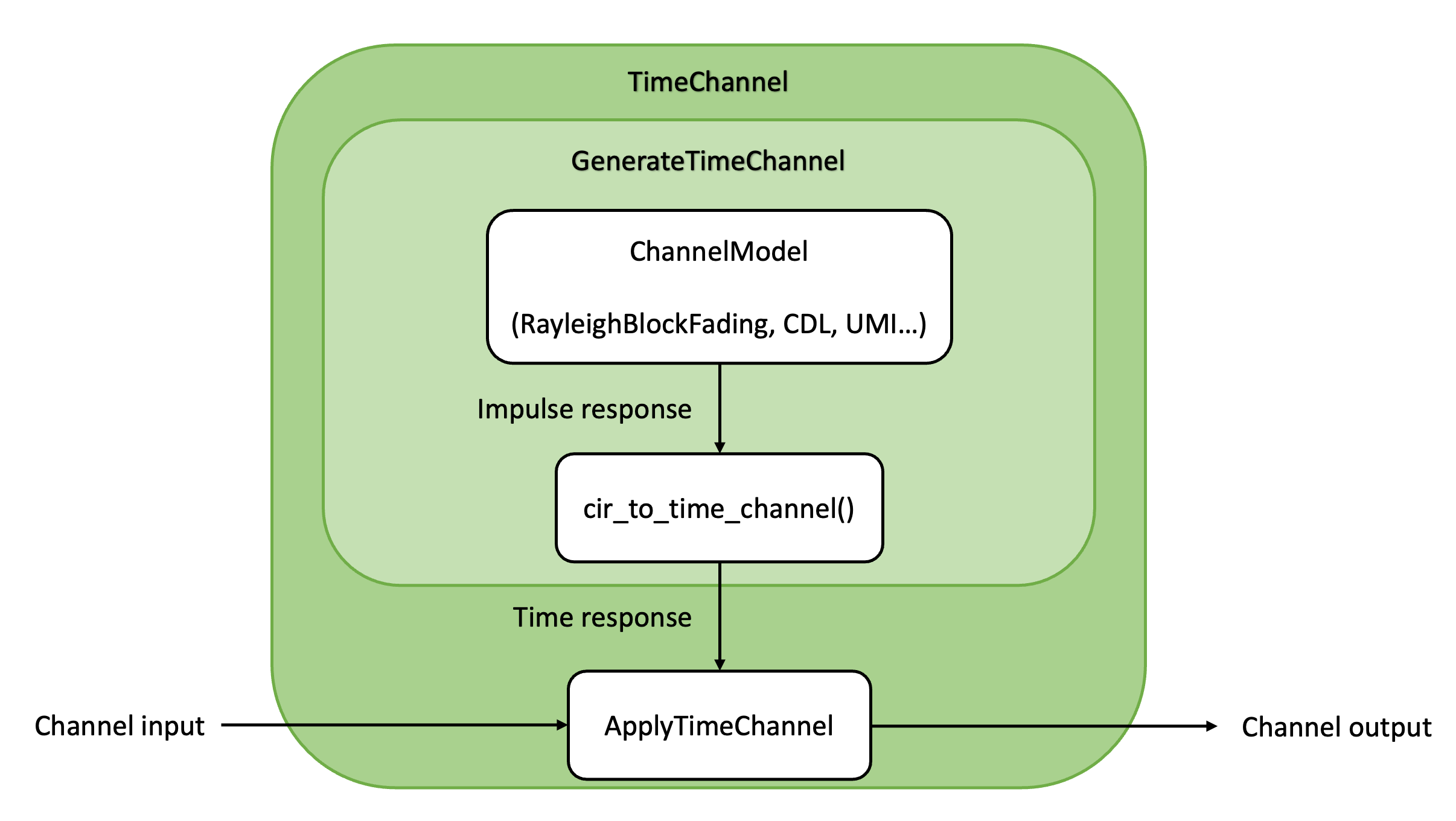
Fig. 10 Channel module architecture for time domain simulations.
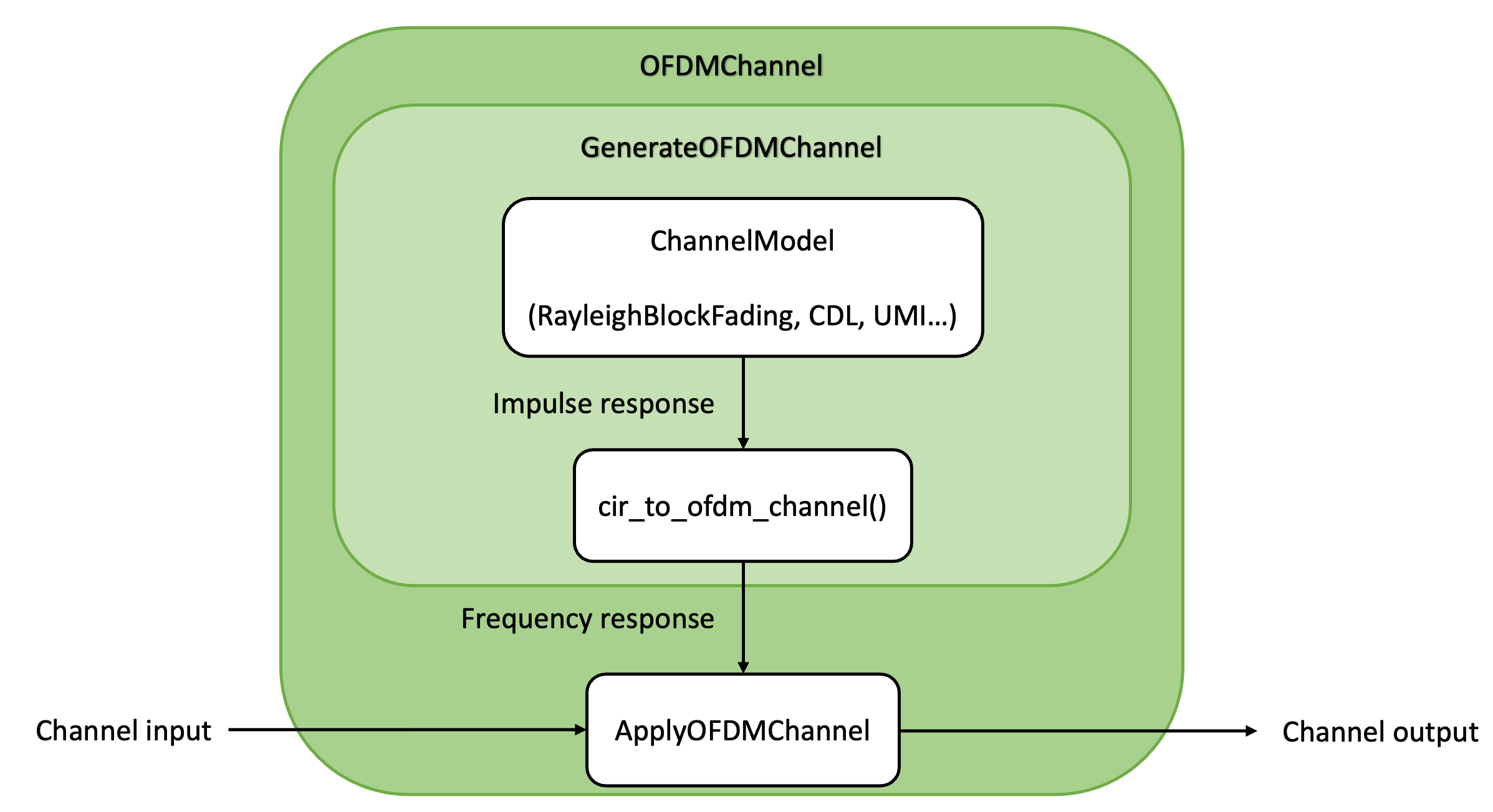
Fig. 11 Channel module architecture for simulations assuming OFDM waveform.
A channel model generate CIRs from which channel responses in the time domain
or in the frequency domain are computed using the
cir_to_time_channel() or
cir_to_ofdm_channel() functions, respectively.
If one does not need access to the raw CIRs, the
GenerateTimeChannel and
GenerateOFDMChannel classes can be used to conveniently
sample CIRs and generate channel responses in the desired domain.
Once the channel responses in the time or frequency domain are computed, they
can be applied to the channel input using the
ApplyTimeChannel or
ApplyOFDMChannel Keras layers.
The following code snippets show how to setup and run a Rayleigh block fading
model assuming an OFDM waveform, and without accessing the CIRs or
channel responses.
This is the easiest way to setup a channel model.
Setting-up other models is done in a similar way, except for
AWGN (see the AWGN
class documentation).
rayleigh = RayleighBlockFading(num_rx = 1,
num_rx_ant = 32,
num_tx = 4,
num_tx_ant = 2)
channel = OFDMChannel(channel_model = rayleigh,
resource_grid = rg)
where rg is an instance of ResourceGrid.
Running the channel model is done as follows:
# x is the channel input
# no is the noise variance
y = channel([x, no])
To use the time domain representation of the channel, one can use
TimeChannel instead of
OFDMChannel.
If access to the channel responses is needed, one can separate their generation from their application to the channel input by setting up the channel model as follows:
rayleigh = RayleighBlockFading(num_rx = 1,
num_rx_ant = 32,
num_tx = 4,
num_tx_ant = 2)
generate_channel = GenerateOFDMChannel(channel_model = rayleigh,
resource_grid = rg)
apply_channel = ApplyOFDMChannel()
where rg is an instance of ResourceGrid.
Running the channel model is done as follows:
# Generate a batch of channel responses
h = generate_channel(batch_size)
# Apply the channel
# x is the channel input
# no is the noise variance
y = apply_channel([x, h, no])
Generating and applying the channel in the time domain can be achieved by using
GenerateTimeChannel and
ApplyTimeChannel instead of
GenerateOFDMChannel and
ApplyOFDMChannel, respectively.
To access the CIRs, setting up the channel can be done as follows:
rayleigh = RayleighBlockFading(num_rx = 1,
num_rx_ant = 32,
num_tx = 4,
num_tx_ant = 2)
apply_channel = ApplyOFDMChannel()
and running the channel model as follows:
cir = rayleigh(batch_size)
h = cir_to_ofdm_channel(frequencies, *cir)
y = apply_channel([x, h, no])
where frequencies are the subcarrier frequencies in the baseband, which can
be computed using the subcarrier_frequencies() utility
function.
Applying the channel in the time domain can be done by using
cir_to_time_channel() and
ApplyTimeChannel instead of
cir_to_ofdm_channel() and
ApplyOFDMChannel, respectively.
For the purpose of the present document, the following symbols apply:
\(N_T (u)\) |
Number of transmitters (transmitter index) |
\(N_R (v)\) |
Number of receivers (receiver index) |
\(N_{TA} (k)\) |
Number of antennas per transmitter (transmit antenna index) |
\(N_{RA} (l)\) |
Number of antennas per receiver (receive antenna index) |
\(N_S (s)\) |
Number of OFDM symbols (OFDM symbol index) |
\(N_F (n)\) |
Number of subcarriers (subcarrier index) |
\(N_B (b)\) |
Number of time samples forming the channel input (baseband symbol index) |
\(L_{\text{min}}\) |
Smallest time-lag for the discrete complex baseband channel |
\(L_{\text{max}}\) |
Largest time-lag for the discrete complex baseband channel |
\(M (m)\) |
Number of paths (clusters) forming a power delay profile (path index) |
\(\tau_m(t)\) |
\(m^{th}\) path (cluster) delay at time step \(t\) |
\(a_m(t)\) |
\(m^{th}\) path (cluster) complex coefficient at time step \(t\) |
\(\Delta_f\) |
Subcarrier spacing |
\(W\) |
Bandwidth |
\(N_0\) |
Noise variance |
All transmitters are equipped with \(N_{TA}\) antennas and all receivers with \(N_{RA}\) antennas.
A channel model, such as RayleighBlockFading or
UMi, is used to generate for each link between
antenna \(k\) of transmitter \(u\) and antenna \(l\) of receiver
\(v\) a power delay profile
\((a_{u, k, v, l, m}(t), \tau_{u, v, m}), 0 \leq m \leq M-1\).
The delays are assumed not to depend on time \(t\), and transmit and receive
antennas \(k\) and \(l\).
Such a power delay profile corresponds to the channel impulse response
where \(\delta(\cdot)\) is the Dirac delta measure. For example, in the case of Rayleigh block fading, the power delay profiles are time-invariant and such that for every link \((u, k, v, l)\)
3GPP channel models use the procedure depicted in [TR38901] to generate power delay profiles. With these models, the power delay profiles are time-variant in the event of mobility.
AWGN
- class sionna.channel.AWGN(dtype=tf.complex64, **kwargs)[source]
Add complex AWGN to the inputs with a certain variance.
This class inherits from the Keras Layer class and can be used as layer in a Keras model.
This layer adds complex AWGN noise with variance
noto the input. The noise has varianceno/2per real dimension. It can be either a scalar or a tensor which can be broadcast to the shape of the input.Example
Setting-up:
>>> awgn_channel = AWGN()
Running:
>>> # x is the channel input >>> # no is the noise variance >>> y = awgn_channel((x, no))
- Parameters:
dtype (Complex tf.DType) – Defines the datatype for internal calculations and the output dtype. Defaults to tf.complex64.
- Input:
(x, no) – Tuple:
x (Tensor, tf.complex) – Channel input
no (Scalar or Tensor, tf.float) – Scalar or tensor whose shape can be broadcast to the shape of
x. The noise powernois per complex dimension. Ifnois a scalar, noise of the same variance will be added to the input. Ifnois a tensor, it must have a shape that can be broadcast to the shape ofx. This allows, e.g., adding noise of different variance to each example in a batch. Ifnohas a lower rank thanx, thennowill be broadcast to the shape ofxby adding dummy dimensions after the last axis.
- Output:
y (Tensor with same shape as
x, tf.complex) – Channel output
Flat-fading channel
FlatFadingChannel
- class sionna.channel.FlatFadingChannel(num_tx_ant, num_rx_ant, spatial_corr=None, add_awgn=True, return_channel=False, dtype=tf.complex64, **kwargs)[source]
Applies random channel matrices to a vector input and adds AWGN.
This class combines
GenerateFlatFadingChannelandApplyFlatFadingChanneland computes the output of a flat-fading channel with AWGN.For a given batch of input vectors \(\mathbf{x}\in\mathbb{C}^{K}\), the output is
\[\mathbf{y} = \mathbf{H}\mathbf{x} + \mathbf{n}\]where \(\mathbf{H}\in\mathbb{C}^{M\times K}\) are randomly generated flat-fading channel matrices and \(\mathbf{n}\in\mathbb{C}^{M}\sim\mathcal{CN}(0, N_o\mathbf{I})\) is an AWGN vector that is optionally added.
A
SpatialCorrelationcan be configured and the channel realizations optionally returned. This is useful to simulate receiver algorithms with perfect channel knowledge.- Parameters:
num_tx_ant (int) – Number of transmit antennas.
num_rx_ant (int) – Number of receive antennas.
spatial_corr (SpatialCorrelation, None) – An instance of
SpatialCorrelationor None. Defaults to None.add_awgn (bool) – Indicates if AWGN noise should be added to the output. Defaults to True.
return_channel (bool) – Indicates if the channel realizations should be returned. Defaults to False.
dtype (tf.complex64, tf.complex128) – The dtype of the output. Defaults to tf.complex64.
- Input:
(x, no) – Tuple or Tensor:
x ([batch_size, num_tx_ant], tf.complex) – Tensor of transmit vectors.
no (Scalar of Tensor, tf.float) – The noise power
nois per complex dimension. Only required ifadd_awgn==True. Will be broadcast to the dimensions of the channel output if needed. For more details, seeAWGN.
- Output:
(y, h) – Tuple or Tensor:
y ([batch_size, num_rx_ant],
dtype) – Channel output.h ([batch_size, num_rx_ant, num_tx_ant],
dtype) – Channel realizations. Will only be returned ifreturn_channel==True.
- property apply
Calls the internal
ApplyFlatFadingChannel.
- property generate
Calls the internal
GenerateFlatFadingChannel.
- property spatial_corr
The
SpatialCorrelationto be used.
GenerateFlatFadingChannel
- class sionna.channel.GenerateFlatFadingChannel(num_tx_ant, num_rx_ant, spatial_corr=None, dtype=tf.complex64, **kwargs)[source]
Generates tensors of flat-fading channel realizations.
This class generates batches of random flat-fading channel matrices. A spatial correlation can be applied.
- Parameters:
num_tx_ant (int) – Number of transmit antennas.
num_rx_ant (int) – Number of receive antennas.
spatial_corr (SpatialCorrelation, None) – An instance of
SpatialCorrelationor None. Defaults to None.dtype (tf.complex64, tf.complex128) – The dtype of the output. Defaults to tf.complex64.
- Input:
batch_size (int) – The batch size, i.e., the number of channel matrices to generate.
- Output:
h ([batch_size, num_rx_ant, num_tx_ant],
dtype) – Batch of random flat fading channel matrices.
- property spatial_corr
The
SpatialCorrelationto be used.
ApplyFlatFadingChannel
- class sionna.channel.ApplyFlatFadingChannel(add_awgn=True, dtype=tf.complex64, **kwargs)[source]
Applies given channel matrices to a vector input and adds AWGN.
This class applies a given tensor of flat-fading channel matrices to an input tensor. AWGN noise can be optionally added. Mathematically, for channel matrices \(\mathbf{H}\in\mathbb{C}^{M\times K}\) and input \(\mathbf{x}\in\mathbb{C}^{K}\), the output is
\[\mathbf{y} = \mathbf{H}\mathbf{x} + \mathbf{n}\]where \(\mathbf{n}\in\mathbb{C}^{M}\sim\mathcal{CN}(0, N_o\mathbf{I})\) is an AWGN vector that is optionally added.
- Parameters:
add_awgn (bool) – Indicates if AWGN noise should be added to the output. Defaults to True.
dtype (tf.complex64, tf.complex128) – The dtype of the output. Defaults to tf.complex64.
- Input:
(x, h, no) – Tuple:
x ([batch_size, num_tx_ant], tf.complex) – Tensor of transmit vectors.
h ([batch_size, num_rx_ant, num_tx_ant], tf.complex) – Tensor of channel realizations. Will be broadcast to the dimensions of
xif needed.no (Scalar or Tensor, tf.float) – The noise power
nois per complex dimension. Only required ifadd_awgn==True. Will be broadcast to the shape ofy. For more details, seeAWGN.
- Output:
y ([batch_size, num_rx_ant],
dtype) – Channel output.
SpatialCorrelation
- class sionna.channel.SpatialCorrelation[source]
Abstract class that defines an interface for spatial correlation functions.
The
FlatFadingChannelmodel can be configured with a spatial correlation model.- Input:
h (tf.complex) – Tensor of arbitrary shape containing spatially uncorrelated channel coefficients
- Output:
h_corr (tf.complex) – Tensor of the same shape and dtype as
hcontaining the spatially correlated channel coefficients.
KroneckerModel
- class sionna.channel.KroneckerModel(r_tx=None, r_rx=None)[source]
Kronecker model for spatial correlation.
Given a batch of matrices \(\mathbf{H}\in\mathbb{C}^{M\times K}\), \(\mathbf{R}_\text{tx}\in\mathbb{C}^{K\times K}\), and \(\mathbf{R}_\text{rx}\in\mathbb{C}^{M\times M}\), this function will generate the following output:
\[\mathbf{H}_\text{corr} = \mathbf{R}^{\frac12}_\text{rx} \mathbf{H} \mathbf{R}^{\frac12}_\text{tx}\]Note that \(\mathbf{R}_\text{tx}\in\mathbb{C}^{K\times K}\) and \(\mathbf{R}_\text{rx}\in\mathbb{C}^{M\times M}\) must be positive semi-definite, such as the ones generated by
exp_corr_mat().- Parameters:
r_tx ([..., K, K], tf.complex) – Tensor containing the transmit correlation matrices. If the rank of
r_txis smaller than that of the inputh, it will be broadcast.r_rx ([..., M, M], tf.complex) – Tensor containing the receive correlation matrices. If the rank of
r_rxis smaller than that of the inputh, it will be broadcast.
- Input:
h ([…, M, K], tf.complex) – Tensor containing spatially uncorrelated channel coeffficients.
- Output:
h_corr ([…, M, K], tf.complex) – Tensor containing the spatially correlated channel coefficients.
- property r_rx
Tensor containing the receive correlation matrices.
Note
If you want to set this property in Graph mode with XLA, i.e., within a function that is decorated with
@tf.function(jit_compile=True), you must setsionna.Config.xla_compat=true. Seexla_compat.
- property r_tx
Tensor containing the transmit correlation matrices.
Note
If you want to set this property in Graph mode with XLA, i.e., within a function that is decorated with
@tf.function(jit_compile=True), you must setsionna.Config.xla_compat=true. Seexla_compat.
PerColumnModel
- class sionna.channel.PerColumnModel(r_rx)[source]
Per-column model for spatial correlation.
Given a batch of matrices \(\mathbf{H}\in\mathbb{C}^{M\times K}\) and correlation matrices \(\mathbf{R}_k\in\mathbb{C}^{M\times M}, k=1,\dots,K\), this function will generate the output \(\mathbf{H}_\text{corr}\in\mathbb{C}^{M\times K}\), with columns
\[\mathbf{h}^\text{corr}_k = \mathbf{R}^{\frac12}_k \mathbf{h}_k,\quad k=1, \dots, K\]where \(\mathbf{h}_k\) is the kth column of \(\mathbf{H}\). Note that all \(\mathbf{R}_k\in\mathbb{C}^{M\times M}\) must be positive semi-definite, such as the ones generated by
one_ring_corr_mat().This model is typically used to simulate a MIMO channel between multiple single-antenna users and a base station with multiple antennas. The resulting SIMO channel for each user has a different spatial correlation.
- Parameters:
r_rx ([..., M, M], tf.complex) – Tensor containing the receive correlation matrices. If the rank of
r_rxis smaller than that of the inputh, it will be broadcast. For a typically use of this model,r_rxhas shape […, K, M, M], i.e., a different correlation matrix for each column ofh.- Input:
h ([…, M, K], tf.complex) – Tensor containing spatially uncorrelated channel coeffficients.
- Output:
h_corr ([…, M, K], tf.complex) – Tensor containing the spatially correlated channel coefficients.
- property r_rx
Tensor containing the receive correlation matrices.
Note
If you want to set this property in Graph mode with XLA, i.e., within a function that is decorated with
@tf.function(jit_compile=True), you must setsionna.Config.xla_compat=true. Seexla_compat.
Channel model interface
- class sionna.channel.ChannelModel[source]
Abstract class that defines an interface for channel models.
Any channel model which generates channel impulse responses must implement this interface. All the channel models available in Sionna, such as
RayleighBlockFadingorTDL, implement this interface.Remark: Some channel models only require a subset of the input parameters.
- Input:
batch_size (int) – Batch size
num_time_steps (int) – Number of time steps
sampling_frequency (float) – Sampling frequency [Hz]
- Output:
a ([batch size, num_rx, num_rx_ant, num_tx, num_tx_ant, num_paths, num_time_steps], tf.complex) – Path coefficients
tau ([batch size, num_rx, num_tx, num_paths], tf.float) – Path delays [s]
Time domain channel
The model of the channel in the time domain assumes pulse shaping and receive filtering are performed using a conventional sinc filter (see, e.g., [Tse]). Using sinc for transmit and receive filtering, the discrete-time domain received signal at time step \(b\) is
where \(x_{u, k, b}\) is the baseband symbol transmitted by transmitter \(u\) on antenna \(k\) and at time step \(b\), \(w_{v, l, b} \sim \mathcal{CN}\left(0,N_0\right)\) the additive white Gaussian noise, and \(\bar{h}_{u, k, v, l, b, \ell}\) the channel filter tap at time step \(b\) and for time-lag \(\ell\), which is given by
Note
The two parameters \(L_{\text{min}}\) and \(L_{\text{max}}\) control the smallest
and largest time-lag for the discrete-time channel model, respectively.
They are set when instantiating TimeChannel,
GenerateTimeChannel, and when calling the utility
function cir_to_time_channel().
Because the sinc filter is neither time-limited nor causal, the discrete-time
channel model is not causal. Therefore, ideally, one would set
\(L_{\text{min}} = -\infty\) and \(L_{\text{max}} = +\infty\).
In practice, however, these two parameters need to be set to reasonable
finite values. Values for these two parameters can be computed using the
time_lag_discrete_time_channel() utility function from
a given bandwidth and maximum delay spread.
This function returns \(-6\) for \(L_{\text{min}}\). \(L_{\text{max}}\) is computed
from the specified bandwidth and maximum delay spread, which default value is
\(3 \mu s\). These values for \(L_{\text{min}}\) and the maximum delay spread
were found to be valid for all the models available in Sionna when an RMS delay
spread of 100ns is assumed.
TimeChannel
- class sionna.channel.TimeChannel(channel_model, bandwidth, num_time_samples, maximum_delay_spread=3e-6, l_min=None, l_max=None, normalize_channel=False, add_awgn=True, return_channel=False, dtype=tf.complex64, **kwargs)[source]
Generate channel responses and apply them to channel inputs in the time domain.
This class inherits from the Keras Layer class and can be used as layer in a Keras model.
The channel output consists of
num_time_samples+l_max-l_mintime samples, as it is the result of filtering the channel input of lengthnum_time_sampleswith the time-variant channel filter of lengthl_max-l_min+ 1. In the case of a single-input single-output link and given a sequence of channel inputs \(x_0,\cdots,x_{N_B}\), where \(N_B\) isnum_time_samples, this layer outputs\[y_b = \sum_{\ell = L_{\text{min}}}^{L_{\text{max}}} x_{b-\ell} \bar{h}_{b,\ell} + w_b\]where \(L_{\text{min}}\) corresponds
l_min, \(L_{\text{max}}\) tol_max, \(w_b\) to the additive noise, and \(\bar{h}_{b,\ell}\) to the \(\ell^{th}\) tap of the \(b^{th}\) channel sample. This layer outputs \(y_b\) for \(b\) ranging from \(L_{\text{min}}\) to \(N_B + L_{\text{max}} - 1\), and \(x_{b}\) is set to 0 for \(b < 0\) or \(b \geq N_B\). The channel taps \(\bar{h}_{b,\ell}\) are computed assuming a sinc filter is used for pulse shaping and receive filtering. Therefore, given a channel impulse response \((a_{m}(t), \tau_{m}), 0 \leq m \leq M-1\), generated by thechannel_model, the channel taps are computed as follows:\[\bar{h}_{b, \ell} = \sum_{m=0}^{M-1} a_{m}\left(\frac{b}{W}\right) \text{sinc}\left( \ell - W\tau_{m} \right)\]for \(\ell\) ranging from
l_mintol_max, and where \(W\) is thebandwidth.For multiple-input multiple-output (MIMO) links, the channel output is computed for each antenna of each receiver and by summing over all the antennas of all transmitters.
- Parameters:
channel_model (
ChannelModelobject) – An instance of aChannelModel, such asRayleighBlockFadingorUMi.bandwidth (float) – Bandwidth (\(W\)) [Hz]
num_time_samples (int) – Number of time samples forming the channel input (\(N_B\))
maximum_delay_spread (float) – Maximum delay spread [s]. Used to compute the default value of
l_maxifl_maxis set to None. If a value is given forl_max, this parameter is not used. It defaults to 3us, which was found to be large enough to include most significant paths with all channel models included in Sionna assuming a nominal delay spread of 100ns.l_min (int) – Smallest time-lag for the discrete complex baseband channel (\(L_{\text{min}}\)). If set to None, defaults to the value given by
time_lag_discrete_time_channel().l_max (int) – Largest time-lag for the discrete complex baseband channel (\(L_{\text{max}}\)). If set to None, it is computed from
bandwidthandmaximum_delay_spreadusingtime_lag_discrete_time_channel(). If it is not set to None, then the parametermaximum_delay_spreadis not used.add_awgn (bool) – If set to False, no white Gaussian noise is added. Defaults to True.
normalize_channel (bool) – If set to True, the channel is normalized over the block size to ensure unit average energy per time step. Defaults to False.
return_channel (bool) – If set to True, the channel response is returned in addition to the channel output. Defaults to False.
dtype (tf.DType) – Complex datatype to use for internal processing and output. Defaults to tf.complex64.
- Input:
(x, no) or x – Tuple or Tensor:
x ([batch size, num_tx, num_tx_ant, num_time_samples], tf.complex) – Channel inputs
no (Scalar or Tensor, tf.float) – Scalar or tensor whose shape can be broadcast to the shape of the channel outputs: [batch size, num_rx, num_rx_ant, num_time_samples]. Only required if
add_awgnis set to True. The noise powernois per complex dimension. Ifnois a scalar, noise of the same variance will be added to the outputs. Ifnois a tensor, it must have a shape that can be broadcast to the shape of the channel outputs. This allows, e.g., adding noise of different variance to each example in a batch. Ifnohas a lower rank than the channel outputs, thennowill be broadcast to the shape of the channel outputs by adding dummy dimensions after the last axis.
- Output:
y ([batch size, num_rx, num_rx_ant, num_time_samples + l_max - l_min], tf.complex) – Channel outputs The channel output consists of
num_time_samples+l_max-l_mintime samples, as it is the result of filtering the channel input of lengthnum_time_sampleswith the time-variant channel filter of lengthl_max-l_min+ 1.h_time ([batch size, num_rx, num_rx_ant, num_tx, num_tx_ant, num_time_samples + l_max - l_min, l_max - l_min + 1], tf.complex) – (Optional) Channel responses. Returned only if
return_channelis set to True. For each batch example,num_time_samples+l_max-l_mintime steps of the channel realizations are generated to filter the channel input.
GenerateTimeChannel
- class sionna.channel.GenerateTimeChannel(channel_model, bandwidth, num_time_samples, l_min, l_max, normalize_channel=False)[source]
Generate channel responses in the time domain.
For each batch example,
num_time_samples+l_max-l_mintime steps of a channel realization are generated by this layer. These can be used to filter a channel input of lengthnum_time_samplesusing theApplyTimeChannellayer.The channel taps \(\bar{h}_{b,\ell}\) (
h_time) returned by this layer are computed assuming a sinc filter is used for pulse shaping and receive filtering. Therefore, given a channel impulse response \((a_{m}(t), \tau_{m}), 0 \leq m \leq M-1\), generated by thechannel_model, the channel taps are computed as follows:\[\bar{h}_{b, \ell} = \sum_{m=0}^{M-1} a_{m}\left(\frac{b}{W}\right) \text{sinc}\left( \ell - W\tau_{m} \right)\]for \(\ell\) ranging from
l_mintol_max, and where \(W\) is thebandwidth.- Parameters:
channel_model (
ChannelModelobject) – An instance of aChannelModel, such asRayleighBlockFadingorUMi.bandwidth (float) – Bandwidth (\(W\)) [Hz]
num_time_samples (int) – Number of time samples forming the channel input (\(N_B\))
l_min (int) – Smallest time-lag for the discrete complex baseband channel (\(L_{\text{min}}\))
l_max (int) – Largest time-lag for the discrete complex baseband channel (\(L_{\text{max}}\))
normalize_channel (bool) – If set to True, the channel is normalized over the block size to ensure unit average energy per time step. Defaults to False.
- Input:
batch_size (int) – Batch size. Defaults to None for channel models that do not require this paranmeter.
- Output:
h_time ([batch size, num_rx, num_rx_ant, num_tx, num_tx_ant, num_time_samples + l_max - l_min, l_max - l_min + 1], tf.complex) – Channel responses. For each batch example,
num_time_samples+l_max-l_mintime steps of a channel realization are generated by this layer. These can be used to filter a channel input of lengthnum_time_samplesusing theApplyTimeChannellayer.
ApplyTimeChannel
- class sionna.channel.ApplyTimeChannel(num_time_samples, l_tot, add_awgn=True, dtype=tf.complex64, **kwargs)[source]
Apply time domain channel responses
h_timeto channel inputsx, by filtering the channel inputs with time-variant channel responses.This class inherits from the Keras Layer class and can be used as layer in a Keras model.
For each batch example,
num_time_samples+l_tot- 1 time steps of a channel realization are required to filter the channel inputs.The channel output consists of
num_time_samples+l_tot- 1 time samples, as it is the result of filtering the channel input of lengthnum_time_sampleswith the time-variant channel filter of lengthl_tot. In the case of a single-input single-output link and given a sequence of channel inputs \(x_0,\cdots,x_{N_B}\), where \(N_B\) isnum_time_samples, this layer outputs\[y_b = \sum_{\ell = 0}^{L_{\text{tot}}} x_{b-\ell} \bar{h}_{b,\ell} + w_b\]where \(L_{\text{tot}}\) corresponds
l_tot, \(w_b\) to the additive noise, and \(\bar{h}_{b,\ell}\) to the \(\ell^{th}\) tap of the \(b^{th}\) channel sample. This layer outputs \(y_b\) for \(b\) ranging from 0 to \(N_B + L_{\text{tot}} - 1\), and \(x_{b}\) is set to 0 for \(b \geq N_B\).For multiple-input multiple-output (MIMO) links, the channel output is computed for each antenna of each receiver and by summing over all the antennas of all transmitters.
- Parameters:
num_time_samples (int) – Number of time samples forming the channel input (\(N_B\))
l_tot (int) – Length of the channel filter (\(L_{\text{tot}} = L_{\text{max}} - L_{\text{min}} + 1\))
add_awgn (bool) – If set to False, no white Gaussian noise is added. Defaults to True.
dtype (tf.DType) – Complex datatype to use for internal processing and output. Defaults to tf.complex64.
- Input:
(x, h_time, no) or (x, h_time) – Tuple:
x ([batch size, num_tx, num_tx_ant, num_time_samples], tf.complex) – Channel inputs
h_time ([batch size, num_rx, num_rx_ant, num_tx, num_tx_ant, num_time_samples + l_tot - 1, l_tot], tf.complex) – Channel responses. For each batch example,
num_time_samples+l_tot- 1 time steps of a channel realization are required to filter the channel inputs.no (Scalar or Tensor, tf.float) – Scalar or tensor whose shape can be broadcast to the shape of the channel outputs: [batch size, num_rx, num_rx_ant, num_time_samples + l_tot - 1]. Only required if
add_awgnis set to True. The noise powernois per complex dimension. Ifnois a scalar, noise of the same variance will be added to the outputs. Ifnois a tensor, it must have a shape that can be broadcast to the shape of the channel outputs. This allows, e.g., adding noise of different variance to each example in a batch. Ifnohas a lower rank than the channel outputs, thennowill be broadcast to the shape of the channel outputs by adding dummy dimensions after the last axis.
- Output:
y ([batch size, num_rx, num_rx_ant, num_time_samples + l_tot - 1], tf.complex) – Channel outputs. The channel output consists of
num_time_samples+l_tot- 1 time samples, as it is the result of filtering the channel input of lengthnum_time_sampleswith the time-variant channel filter of lengthl_tot.
cir_to_time_channel
- sionna.channel.cir_to_time_channel(bandwidth, a, tau, l_min, l_max, normalize=False)[source]
Compute the channel taps forming the discrete complex-baseband representation of the channel from the channel impulse response (
a,tau).This function assumes that a sinc filter is used for pulse shaping and receive filtering. Therefore, given a channel impulse response \((a_{m}(t), \tau_{m}), 0 \leq m \leq M-1\), the channel taps are computed as follows:
\[\bar{h}_{b, \ell} = \sum_{m=0}^{M-1} a_{m}\left(\frac{b}{W}\right) \text{sinc}\left( \ell - W\tau_{m} \right)\]for \(\ell\) ranging from
l_mintol_max, and where \(W\) is thebandwidth.- Input:
bandwidth (float) – Bandwidth [Hz]
a ([batch size, num_rx, num_rx_ant, num_tx, num_tx_ant, num_paths, num_time_steps], tf.complex) – Path coefficients
tau ([batch size, num_rx, num_tx, num_paths] or [batch size, num_rx, num_rx_ant, num_tx, num_tx_ant, num_paths], tf.float) – Path delays [s]
l_min (int) – Smallest time-lag for the discrete complex baseband channel (\(L_{\text{min}}\))
l_max (int) – Largest time-lag for the discrete complex baseband channel (\(L_{\text{max}}\))
normalize (bool) – If set to True, the channel is normalized over the block size to ensure unit average energy per time step. Defaults to False.
- Output:
hm ([batch size, num_rx, num_rx_ant, num_tx, num_tx_ant, num_time_steps, l_max - l_min + 1], tf.complex) – Channel taps coefficients
time_to_ofdm_channel
- sionna.channel.time_to_ofdm_channel(h_t, rg, l_min)[source]
Compute the channel frequency response from the discrete complex-baseband channel impulse response.
Given a discrete complex-baseband channel impulse response \(\bar{h}_{b,\ell}\), for \(\ell\) ranging from \(L_\text{min}\le 0\) to \(L_\text{max}\), the discrete channel frequency response is computed as
\[\hat{h}_{b,n} = \sum_{k=0}^{L_\text{max}} \bar{h}_{b,k} e^{-j \frac{2\pi kn}{N}} + \sum_{k=L_\text{min}}^{-1} \bar{h}_{b,k} e^{-j \frac{2\pi n(N+k)}{N}}, \quad n=0,\dots,N-1\]where \(N\) is the FFT size and \(b\) is the time step.
This function only produces one channel frequency response per OFDM symbol, i.e., only values of \(b\) corresponding to the start of an OFDM symbol (after cyclic prefix removal) are considered.
- Input:
h_t ([…num_time_steps,l_max-l_min+1], tf.complex) – Tensor of discrete complex-baseband channel impulse responses
resource_grid (
ResourceGrid) – Resource gridl_min (int) – Smallest time-lag for the discrete complex baseband channel impulse response (\(L_{\text{min}}\))
- Output:
h_f ([…,num_ofdm_symbols,fft_size], tf.complex) – Tensor of discrete complex-baseband channel frequency responses
Note
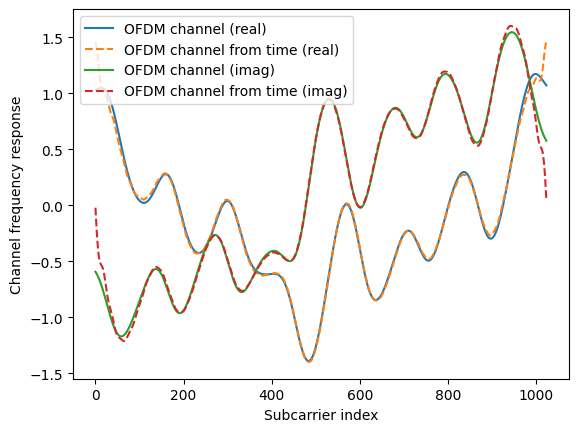
Note that the result of this function is generally different from the output of
cir_to_ofdm_channel()because the discrete complex-baseband channel impulse response is truncated (seecir_to_time_channel()). This effect can be observed in the example below.Examples
# Setup resource grid and channel model sm = StreamManagement(np.array([[1]]), 1) rg = ResourceGrid(num_ofdm_symbols=1, fft_size=1024, subcarrier_spacing=15e3) tdl = TDL("A", 100e-9, 3.5e9) # Generate CIR cir = tdl(batch_size=1, num_time_steps=1, sampling_frequency=rg.bandwidth) # Generate OFDM channel from CIR frequencies = subcarrier_frequencies(rg.fft_size, rg.subcarrier_spacing) h_freq = tf.squeeze(cir_to_ofdm_channel(frequencies, *cir, normalize=True)) # Generate time channel from CIR l_min, l_max = time_lag_discrete_time_channel(rg.bandwidth) h_time = cir_to_time_channel(rg.bandwidth, *cir, l_min=l_min, l_max=l_max, normalize=True) # Generate OFDM channel from time channel h_freq_hat = tf.squeeze(time_to_ofdm_channel(h_time, rg, l_min)) # Visualize results plt.figure() plt.plot(np.real(h_freq), "-") plt.plot(np.real(h_freq_hat), "--") plt.plot(np.imag(h_freq), "-") plt.plot(np.imag(h_freq_hat), "--") plt.xlabel("Subcarrier index") plt.ylabel(r"Channel frequency response") plt.legend(["OFDM Channel (real)", "OFDM Channel from time (real)", "OFDM Channel (imag)", "OFDM Channel from time (imag)"])
Channel with OFDM waveform
To implement the channel response assuming an OFDM waveform, it is assumed that the power delay profiles are invariant over the duration of an OFDM symbol. Moreover, it is assumed that the duration of the cyclic prefix (CP) equals at least the maximum delay spread. These assumptions are common in the literature, as they enable modeling of the channel transfer function in the frequency domain as a single-tap channel.
For every link \((u, k, v, l)\) and resource element \((s,n)\), the frequency channel response is obtained by computing the Fourier transform of the channel response at the subcarrier frequencies, i.e.,
where \(s\) is used as time step to indicate that the channel response can change from one OFDM symbol to the next in the event of mobility, even if it is assumed static over the duration of an OFDM symbol.
For every receive antenna \(l\) of every receiver \(v\), the received signal \(y_{v, l, s, n}`\) for resource element \((s, n)\) is computed by
where \(x_{u, k, s, n}\) is the baseband symbol transmitted by transmitter \(u`\) on antenna \(k\) and resource element \((s, n)\), and \(w_{v, l, s, n} \sim \mathcal{CN}\left(0,N_0\right)\) the additive white Gaussian noise.
Note
This model does not account for intersymbol interference (ISI) nor
intercarrier interference (ICI). To model the ICI due to channel aging over
the duration of an OFDM symbol or the ISI due to a delay spread exceeding the
CP duration, one would need to simulate the channel in the time domain.
This can be achieved by using the OFDMModulator and
OFDMDemodulator layers, and the
time domain channel model.
By doing so, one performs inverse discrete Fourier transform (IDFT) on
the transmitter side and discrete Fourier transform (DFT) on the receiver side
on top of a single-carrier sinc-shaped waveform.
This is equivalent to
simulating the channel in the frequency domain if no
ISI nor ICI is assumed, but allows the simulation of these effects in the
event of a non-stationary channel or long delay spreads.
Note that simulating the channel in the time domain is typically significantly
more computationally demanding that simulating the channel in the frequency
domain.
OFDMChannel
- class sionna.channel.OFDMChannel(channel_model, resource_grid, add_awgn=True, normalize_channel=False, return_channel=False, dtype=tf.complex64, **kwargs)[source]
Generate channel frequency responses and apply them to channel inputs assuming an OFDM waveform with no ICI nor ISI.
This class inherits from the Keras Layer class and can be used as layer in a Keras model.
For each OFDM symbol \(s\) and subcarrier \(n\), the channel output is computed as follows:
\[y_{s,n} = \widehat{h}_{s, n} x_{s,n} + w_{s,n}\]where \(y_{s,n}\) is the channel output computed by this layer, \(\widehat{h}_{s, n}\) the frequency channel response, \(x_{s,n}\) the channel input
x, and \(w_{s,n}\) the additive noise.For multiple-input multiple-output (MIMO) links, the channel output is computed for each antenna of each receiver and by summing over all the antennas of all transmitters.
The channel frequency response for the \(s^{th}\) OFDM symbol and \(n^{th}\) subcarrier is computed from a given channel impulse response \((a_{m}(t), \tau_{m}), 0 \leq m \leq M-1\) generated by the
channel_modelas follows:\[\widehat{h}_{s, n} = \sum_{m=0}^{M-1} a_{m}(s) e^{-j2\pi n \Delta_f \tau_{m}}\]where \(\Delta_f\) is the subcarrier spacing, and \(s\) is used as time step to indicate that the channel impulse response can change from one OFDM symbol to the next in the event of mobility, even if it is assumed static over the duration of an OFDM symbol.
- Parameters:
channel_model (
ChannelModelobject) – An instance of aChannelModelobject, such asRayleighBlockFadingorUMi.resource_grid (
ResourceGrid) – Resource gridadd_awgn (bool) – If set to False, no white Gaussian noise is added. Defaults to True.
normalize_channel (bool) – If set to True, the channel is normalized over the resource grid to ensure unit average energy per resource element. Defaults to False.
return_channel (bool) – If set to True, the channel response is returned in addition to the channel output. Defaults to False.
dtype (tf.DType) – Complex datatype to use for internal processing and output. Defaults to tf.complex64.
- Input:
(x, no) or x – Tuple or Tensor:
x ([batch size, num_tx, num_tx_ant, num_ofdm_symbols, fft_size], tf.complex) – Channel inputs
no (Scalar or Tensor, tf.float) – Scalar or tensor whose shape can be broadcast to the shape of the channel outputs: [batch size, num_rx, num_rx_ant, num_ofdm_symbols, fft_size]. Only required if
add_awgnis set to True. The noise powernois per complex dimension. Ifnois a scalar, noise of the same variance will be added to the outputs. Ifnois a tensor, it must have a shape that can be broadcast to the shape of the channel outputs. This allows, e.g., adding noise of different variance to each example in a batch. Ifnohas a lower rank than the channel outputs, thennowill be broadcast to the shape of the channel outputs by adding dummy dimensions after the last axis.
- Output:
y ([batch size, num_rx, num_rx_ant, num_ofdm_symbols, fft_size], tf.complex) – Channel outputs
h_freq ([batch size, num_rx, num_rx_ant, num_tx, num_tx_ant, num_ofdm_symbols, fft_size], tf.complex) – (Optional) Channel frequency responses. Returned only if
return_channelis set to True.
GenerateOFDMChannel
- class sionna.channel.GenerateOFDMChannel(channel_model, resource_grid, normalize_channel=False)[source]
Generate channel frequency responses. The channel impulse response is constant over the duration of an OFDM symbol.
Given a channel impulse response \((a_{m}(t), \tau_{m}), 0 \leq m \leq M-1\), generated by the
channel_model, the channel frequency response for the \(s^{th}\) OFDM symbol and \(n^{th}\) subcarrier is computed as follows:\[\widehat{h}_{s, n} = \sum_{m=0}^{M-1} a_{m}(s) e^{-j2\pi n \Delta_f \tau_{m}}\]where \(\Delta_f\) is the subcarrier spacing, and \(s\) is used as time step to indicate that the channel impulse response can change from one OFDM symbol to the next in the event of mobility, even if it is assumed static over the duration of an OFDM symbol.
- Parameters:
channel_model (
ChannelModelobject) – An instance of aChannelModelobject, such asRayleighBlockFadingorUMi.resource_grid (
ResourceGrid) – Resource gridnormalize_channel (bool) – If set to True, the channel is normalized over the resource grid to ensure unit average energy per resource element. Defaults to False.
dtype (tf.DType) – Complex datatype to use for internal processing and output. Defaults to tf.complex64.
- Input:
batch_size (int) – Batch size. Defaults to None for channel models that do not require this paranmeter.
- Output:
h_freq ([batch size, num_rx, num_rx_ant, num_tx, num_tx_ant, num_ofdm_symbols, num_subcarriers], tf.complex) – Channel frequency responses
ApplyOFDMChannel
- class sionna.channel.ApplyOFDMChannel(add_awgn=True, dtype=tf.complex64, **kwargs)[source]
Apply single-tap channel frequency responses to channel inputs.
This class inherits from the Keras Layer class and can be used as layer in a Keras model.
For each OFDM symbol \(s\) and subcarrier \(n\), the single-tap channel is applied as follows:
\[y_{s,n} = \widehat{h}_{s, n} x_{s,n} + w_{s,n}\]where \(y_{s,n}\) is the channel output computed by this layer, \(\widehat{h}_{s, n}\) the frequency channel response (
h_freq), \(x_{s,n}\) the channel inputx, and \(w_{s,n}\) the additive noise.For multiple-input multiple-output (MIMO) links, the channel output is computed for each antenna of each receiver and by summing over all the antennas of all transmitters.
- Parameters:
add_awgn (bool) – If set to False, no white Gaussian noise is added. Defaults to True.
dtype (tf.DType) – Complex datatype to use for internal processing and output. Defaults to tf.complex64.
- Input:
(x, h_freq, no) or (x, h_freq) – Tuple:
x ([batch size, num_tx, num_tx_ant, num_ofdm_symbols, fft_size], tf.complex) – Channel inputs
h_freq ([batch size, num_rx, num_rx_ant, num_tx, num_tx_ant, num_ofdm_symbols, fft_size], tf.complex) – Channel frequency responses
no (Scalar or Tensor, tf.float) – Scalar or tensor whose shape can be broadcast to the shape of the channel outputs: [batch size, num_rx, num_rx_ant, num_ofdm_symbols, fft_size]. Only required if
add_awgnis set to True. The noise powernois per complex dimension. Ifnois a scalar, noise of the same variance will be added to the outputs. Ifnois a tensor, it must have a shape that can be broadcast to the shape of the channel outputs. This allows, e.g., adding noise of different variance to each example in a batch. Ifnohas a lower rank than the channel outputs, thennowill be broadcast to the shape of the channel outputs by adding dummy dimensions after the last axis.
- Output:
y ([batch size, num_rx, num_rx_ant, num_ofdm_symbols, fft_size], tf.complex) – Channel outputs
cir_to_ofdm_channel
- sionna.channel.cir_to_ofdm_channel(frequencies, a, tau, normalize=False)[source]
Compute the frequency response of the channel at
frequencies.Given a channel impulse response \((a_{m}, \tau_{m}), 0 \leq m \leq M-1\) (inputs
aandtau), the channel frequency response for the frequency \(f\) is computed as follows:\[\widehat{h}(f) = \sum_{m=0}^{M-1} a_{m} e^{-j2\pi f \tau_{m}}\]- Input:
frequencies ([fft_size], tf.float) – Frequencies at which to compute the channel response
a ([batch size, num_rx, num_rx_ant, num_tx, num_tx_ant, num_paths, num_time_steps], tf.complex) – Path coefficients
tau ([batch size, num_rx, num_tx, num_paths] or [batch size, num_rx, num_rx_ant, num_tx, num_tx_ant, num_paths], tf.float) – Path delays
normalize (bool) – If set to True, the channel is normalized over the resource grid to ensure unit average energy per resource element. Defaults to False.
- Output:
h_f ([batch size, num_rx, num_rx_ant, num_tx, num_tx_ant, num_time_steps, fft_size], tf.complex) – Channel frequency responses at
frequencies
Rayleigh block fading
- class sionna.channel.RayleighBlockFading(num_rx, num_rx_ant, num_tx, num_tx_ant, dtype=tf.complex64)[source]
Generate channel impulse responses corresponding to a Rayleigh block fading channel model.
The channel impulse responses generated are formed of a single path with zero delay and a normally distributed fading coefficient. All time steps of a batch example share the same channel coefficient (block fading).
This class can be used in conjunction with the classes that simulate the channel response in time or frequency domain, i.e.,
OFDMChannel,TimeChannel,GenerateOFDMChannel,ApplyOFDMChannel,GenerateTimeChannel,ApplyTimeChannel.- Parameters:
num_rx (int) – Number of receivers (\(N_R\))
num_rx_ant (int) – Number of antennas per receiver (\(N_{RA}\))
num_tx (int) – Number of transmitters (\(N_T\))
num_tx_ant (int) – Number of antennas per transmitter (\(N_{TA}\))
dtype (tf.DType) – Complex datatype to use for internal processing and output. Defaults to tf.complex64.
- Input:
batch_size (int) – Batch size
num_time_steps (int) – Number of time steps
- Output:
a ([batch size, num_rx, num_rx_ant, num_tx, num_tx_ant, num_paths = 1, num_time_steps], tf.complex) – Path coefficients
tau ([batch size, num_rx, num_tx, num_paths = 1], tf.float) – Path delays [s]
3GPP 38.901 channel models
The submodule tr38901 implements 3GPP channel models from [TR38901].
The CDL, UMi, UMa, and RMa
models require setting-up antenna models for the transmitters and
receivers. This is achieved using the
PanelArray class.
The UMi, UMa, and RMa models require setting-up a network topology, specifying, e.g., the user terminals (UTs) and base stations (BSs) locations, the UTs velocities, etc. Utility functions are available to help laying out complex topologies or to quickly setup simple but widely used topologies.
PanelArray
- class sionna.channel.tr38901.PanelArray(num_rows_per_panel, num_cols_per_panel, polarization, polarization_type, antenna_pattern, carrier_frequency, num_rows=1, num_cols=1, panel_vertical_spacing=None, panel_horizontal_spacing=None, element_vertical_spacing=None, element_horizontal_spacing=None, dtype=tf.complex64)[source]
Antenna panel array following the [TR38901] specification.
This class is used to create models of the panel arrays used by the transmitters and receivers and that need to be specified when using the CDL, UMi, UMa, and RMa models.
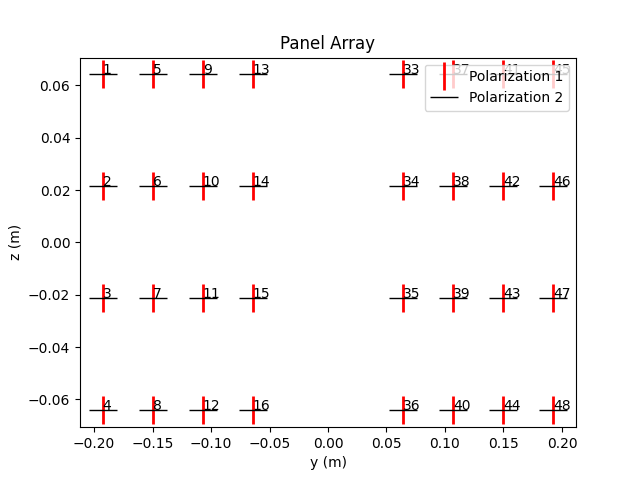
Example
>>> array = PanelArray(num_rows_per_panel = 4, ... num_cols_per_panel = 4, ... polarization = 'dual', ... polarization_type = 'VH', ... antenna_pattern = '38.901', ... carrier_frequency = 3.5e9, ... num_cols = 2, ... panel_horizontal_spacing = 3.) >>> array.show()
- Parameters:
num_rows_per_panel (int) – Number of rows of elements per panel
num_cols_per_panel (int) – Number of columns of elements per panel
polarization (str) – Polarization, either “single” or “dual”
polarization_type (str) – Type of polarization. For single polarization, must be “V” or “H”. For dual polarization, must be “VH” or “cross”.
antenna_pattern (str) – Element radiation pattern, either “omni” or “38.901”
carrier_frequency (float) – Carrier frequency [Hz]
num_rows (int) – Number of rows of panels. Defaults to 1.
num_cols (int) – Number of columns of panels. Defaults to 1.
panel_vertical_spacing (None or float) – Vertical spacing of panels [multiples of wavelength]. Must be greater than the panel width. If set to None (default value), it is set to the panel width + 0.5.
panel_horizontal_spacing (None or float) – Horizontal spacing of panels [in multiples of wavelength]. Must be greater than the panel height. If set to None (default value), it is set to the panel height + 0.5.
element_vertical_spacing (None or float) – Element vertical spacing [multiple of wavelength]. Defaults to 0.5 if set to None.
element_horizontal_spacing (None or float) – Element horizontal spacing [multiple of wavelength]. Defaults to 0.5 if set to None.
dtype (Complex tf.DType) – Defines the datatype for internal calculations and the output dtype. Defaults to tf.complex64.
- property ant_ind_pol1
Indices of antenna elements with the first polarization direction
- property ant_ind_pol2
Indices of antenna elements with the second polarization direction. Only defined with dual polarization.
- property ant_pol1
Field of an antenna element with the first polarization direction
- property ant_pol2
Field of an antenna element with the second polarization direction. Only defined with dual polarization.
- property ant_pos
Positions of the antennas
- property ant_pos_pol1
Positions of the antenna elements with the first polarization direction
- property ant_pos_pol2
Positions of antenna elements with the second polarization direction. Only defined with dual polarization.
- property element_horizontal_spacing
Horizontal spacing between the antenna elements within a panel [multiple of wavelength]
- property element_vertical_spacing
Vertical spacing between the antenna elements within a panel [multiple of wavelength]
- property num_ant
Total number of antenna elements
- property num_cols
Number of columns of panels
- property num_cols_per_panel
Number of columns of elements per panel
- property num_panels
Number of panels
- property num_panels_ant
Number of antenna elements per panel
- property num_rows
Number of rows of panels
- property num_rows_per_panel
Number of rows of elements per panel
- property panel_horizontal_spacing
Horizontal spacing between the panels [multiple of wavelength]
- property panel_vertical_spacing
Vertical spacing between the panels [multiple of wavelength]
- property polarization
Polarization (“single” or “dual”)
- property polarization_type
Polarization type. “V” or “H” for single polarization. “VH” or “cross” for dual polarization.
Antenna
- class sionna.channel.tr38901.Antenna(polarization, polarization_type, antenna_pattern, carrier_frequency, dtype=tf.complex64)[source]
Single antenna following the [TR38901] specification.
This class is a special case of
PanelArray, and can be used in lieu of it.- Parameters:
polarization (str) – Polarization, either “single” or “dual”
polarization_type (str) – Type of polarization. For single polarization, must be “V” or “H”. For dual polarization, must be “VH” or “cross”.
antenna_pattern (str) – Element radiation pattern, either “omni” or “38.901”
carrier_frequency (float) – Carrier frequency [Hz]
dtype (Complex tf.DType) – Defines the datatype for internal calculations and the output dtype. Defaults to tf.complex64.
AntennaArray
- class sionna.channel.tr38901.AntennaArray(num_rows, num_cols, polarization, polarization_type, antenna_pattern, carrier_frequency, vertical_spacing, horizontal_spacing, dtype=tf.complex64)[source]
Antenna array following the [TR38901] specification.
This class is a special case of
PanelArray, and can used in lieu of it.- Parameters:
num_rows (int) – Number of rows of elements
num_cols (int) – Number of columns of elements
polarization (str) – Polarization, either “single” or “dual”
polarization_type (str) – Type of polarization. For single polarization, must be “V” or “H”. For dual polarization, must be “VH” or “cross”.
antenna_pattern (str) – Element radiation pattern, either “omni” or “38.901”
carrier_frequency (float) – Carrier frequency [Hz]
vertical_spacing (None or float) – Element vertical spacing [multiple of wavelength]. Defaults to 0.5 if set to None.
horizontal_spacing (None or float) – Element horizontal spacing [multiple of wavelength]. Defaults to 0.5 if set to None.
dtype (Complex tf.DType) – Defines the datatype for internal calculations and the output dtype. Defaults to tf.complex64.
Tapped delay line (TDL)
- class sionna.channel.tr38901.TDL(model, delay_spread, carrier_frequency, num_sinusoids=20, los_angle_of_arrival=PI / 4., min_speed=0., max_speed=None, num_rx_ant=1, num_tx_ant=1, spatial_corr_mat=None, rx_corr_mat=None, tx_corr_mat=None, dtype=tf.complex64)[source]
Tapped delay line (TDL) channel model from the 3GPP [TR38901] specification.
The power delay profiles (PDPs) are normalized to have a total energy of one.
Channel coefficients are generated using a sum-of-sinusoids model [SoS]. Channel aging is simulated in the event of mobility.
If a minimum speed and a maximum speed are specified such that the maximum speed is greater than the minimum speed, then speeds are randomly and uniformly sampled from the specified interval for each link and each batch example.
The TDL model only works for systems with a single transmitter and a single receiver. The transmitter and receiver can be equipped with multiple antennas. Spatial correlation is simulated through filtering by specified correlation matrices.
The
spatial_corr_matparameter can be used to specify an arbitrary spatial correlation matrix. In particular, it can be used to model correlated cross-polarized transmit and receive antennas as follows (see, e.g., Annex G.2.3.2.1 [TS38141-1]):\[\mathbf{R} = \mathbf{R}_{\text{rx}} \otimes \mathbf{\Gamma} \otimes \mathbf{R}_{\text{tx}}\]where \(\mathbf{R}\) is the spatial correlation matrix
spatial_corr_mat, \(\mathbf{R}_{\text{rx}}\) the spatial correlation matrix at the receiver with same polarization, \(\mathbf{R}_{\text{tx}}\) the spatial correlation matrix at the transmitter with same polarization, and \(\mathbf{\Gamma}\) the polarization correlation matrix. \(\mathbf{\Gamma}\) is 1x1 for single-polarized antennas, 2x2 when only the transmit or receive antennas are cross-polarized, and 4x4 when transmit and receive antennas are cross-polarized.It is also possible not to specify
spatial_corr_mat, but instead the correlation matrices at the receiver and transmitter, using therx_corr_matandtx_corr_matparameters, respectively. This can be useful when single polarized antennas are simulated, and it is also more computationally efficient. This is equivalent to settingspatial_corr_matto :\[\mathbf{R} = \mathbf{R}_{\text{rx}} \otimes \mathbf{R}_{\text{tx}}\]where \(\mathbf{R}_{\text{rx}}\) is the correlation matrix at the receiver
rx_corr_matand \(\mathbf{R}_{\text{tx}}\) the correlation matrix at the transmittertx_corr_mat.Example
The following code snippet shows how to setup a TDL channel model assuming an OFDM waveform:
>>> tdl = TDL(model = "A", ... delay_spread = 300e-9, ... carrier_frequency = 3.5e9, ... min_speed = 0.0, ... max_speed = 3.0) >>> >>> channel = OFDMChannel(channel_model = tdl, ... resource_grid = rg)
where
rgis an instance ofResourceGrid.Notes
The following tables from [TR38901] provide typical values for the delay spread.
Model
Delay spread [ns]
Very short delay spread
\(10\)
Short short delay spread
\(10\)
Nominal delay spread
\(100\)
Long delay spread
\(300\)
Very long delay spread
\(1000\)
Delay spread [ns]
Frequency [GHz]
2
6
15
28
39
60
70
Indoor office
Short delay profile
20
16
16
16
16
16
16
Normal delay profile
39
30
24
20
18
16
16
Long delay profile
59
53
47
43
41
38
37
UMi Street-canyon
Short delay profile
65
45
37
32
30
27
26
Normal delay profile
129
93
76
66
61
55
53
Long delay profile
634
316
307
301
297
293
291
UMa
Short delay profile
93
93
85
80
78
75
74
Normal delay profile
363
363
302
266
249
228
221
Long delay profile
1148
1148
955
841
786
720
698
RMa / RMa O2I
Short delay profile
32
32
N/A
N/A
N/A
N/A
N/A
Normal delay profile
37
37
N/A
N/A
N/A
N/A
N/A
Long delay profile
153
153
N/A
N/A
N/A
N/A
N/A
UMi / UMa O2I
Normal delay profile
242
Long delay profile
616
- Parameters:
model (str) – TDL model to use. Must be one of “A”, “B”, “C”, “D”, “E”, “A30”, “B100”, or “C300”.
delay_spread (float) – RMS delay spread [s]. For the “A30”, “B100”, and “C300” models, the delay spread must be set to 30ns, 100ns, and 300ns, respectively.
carrier_frequency (float) – Carrier frequency [Hz]
num_sinusoids (int) – Number of sinusoids for the sum-of-sinusoids model. Defaults to 20.
los_angle_of_arrival (float) – Angle-of-arrival for LoS path [radian]. Only used with LoS models. Defaults to \(\pi/4\).
min_speed (float) – Minimum speed [m/s]. Defaults to 0.
max_speed (None or float) – Maximum speed [m/s]. If set to None, then
max_speedtakes the same value asmin_speed. Defaults to None.num_rx_ant (int) – Number of receive antennas. Defaults to 1.
num_tx_ant (int) – Number of transmit antennas. Defaults to 1.
spatial_corr_mat ([num_rx_ant*num_tx_ant,num_rx_ant*num_tx_ant], tf.complex or None) – Spatial correlation matrix. If not set to None, then
rx_corr_matandtx_corr_matare ignored and this matrix is used for spatial correlation. If set to None andrx_corr_matandtx_corr_matare also set to None, then no correlation is applied. Defaults to None.rx_corr_mat ([num_rx_ant,num_rx_ant], tf.complex or None) – Spatial correlation matrix for the receiver. If set to None and
spatial_corr_matis also set to None, then no receive correlation is applied. Defaults to None.tx_corr_mat ([num_tx_ant,num_tx_ant], tf.complex or None) – Spatial correlation matrix for the transmitter. If set to None and
spatial_corr_matis also set to None, then no transmit correlation is applied. Defaults to None.dtype (Complex tf.DType) – Defines the datatype for internal calculations and the output dtype. Defaults to tf.complex64.
- Input:
batch_size (int) – Batch size
num_time_steps (int) – Number of time steps
sampling_frequency (float) – Sampling frequency [Hz]
- Output:
a ([batch size, num_rx = 1, num_rx_ant = 1, num_tx = 1, num_tx_ant = 1, num_paths, num_time_steps], tf.complex) – Path coefficients
tau ([batch size, num_rx = 1, num_tx = 1, num_paths], tf.float) – Path delays [s]
- property delay_spread
RMS delay spread [s]
- property delays
Path delays [s]
- property k_factor
K-factor in linear scale. Only available with LoS models.
- property los
True if this is a LoS model. False otherwise.
- property mean_power_los
LoS component power in linear scale. Only available with LoS models.
- property mean_powers
Path powers in linear scale
- property num_clusters
Number of paths (\(M\))
Clustered delay line (CDL)
- class sionna.channel.tr38901.CDL(model, delay_spread, carrier_frequency, ut_array, bs_array, direction, min_speed=0., max_speed=None, dtype=tf.complex64)[source]
Clustered delay line (CDL) channel model from the 3GPP [TR38901] specification.
The power delay profiles (PDPs) are normalized to have a total energy of one.
If a minimum speed and a maximum speed are specified such that the maximum speed is greater than the minimum speed, then UTs speeds are randomly and uniformly sampled from the specified interval for each link and each batch example.
The CDL model only works for systems with a single transmitter and a single receiver. The transmitter and receiver can be equipped with multiple antennas.
Example
The following code snippet shows how to setup a CDL channel model assuming an OFDM waveform:
>>> # Panel array configuration for the transmitter and receiver >>> bs_array = PanelArray(num_rows_per_panel = 4, ... num_cols_per_panel = 4, ... polarization = 'dual', ... polarization_type = 'cross', ... antenna_pattern = '38.901', ... carrier_frequency = 3.5e9) >>> ut_array = PanelArray(num_rows_per_panel = 1, ... num_cols_per_panel = 1, ... polarization = 'single', ... polarization_type = 'V', ... antenna_pattern = 'omni', ... carrier_frequency = 3.5e9) >>> # CDL channel model >>> cdl = CDL(model = "A", >>> delay_spread = 300e-9, ... carrier_frequency = 3.5e9, ... ut_array = ut_array, ... bs_array = bs_array, ... direction = 'uplink') >>> channel = OFDMChannel(channel_model = cdl, ... resource_grid = rg)
where
rgis an instance ofResourceGrid.Notes
The following tables from [TR38901] provide typical values for the delay spread.
Model
Delay spread [ns]
Very short delay spread
\(10\)
Short short delay spread
\(10\)
Nominal delay spread
\(100\)
Long delay spread
\(300\)
Very long delay spread
\(1000\)
Delay spread [ns]
Frequency [GHz]
2
6
15
28
39
60
70
Indoor office
Short delay profile
20
16
16
16
16
16
16
Normal delay profile
39
30
24
20
18
16
16
Long delay profile
59
53
47
43
41
38
37
UMi Street-canyon
Short delay profile
65
45
37
32
30
27
26
Normal delay profile
129
93
76
66
61
55
53
Long delay profile
634
316
307
301
297
293
291
UMa
Short delay profile
93
93
85
80
78
75
74
Normal delay profile
363
363
302
266
249
228
221
Long delay profile
1148
1148
955
841
786
720
698
RMa / RMa O2I
Short delay profile
32
32
N/A
N/A
N/A
N/A
N/A
Normal delay profile
37
37
N/A
N/A
N/A
N/A
N/A
Long delay profile
153
153
N/A
N/A
N/A
N/A
N/A
UMi / UMa O2I
Normal delay profile
242
Long delay profile
616
- Parameters:
model (str) – CDL model to use. Must be one of “A”, “B”, “C”, “D” or “E”.
delay_spread (float) – RMS delay spread [s].
carrier_frequency (float) – Carrier frequency [Hz].
ut_array (PanelArray) – Panel array used by the UTs. All UTs share the same antenna array configuration.
bs_array (PanelArray) – Panel array used by the Bs. All BSs share the same antenna array configuration.
direction (str) – Link direction. Must be either “uplink” or “downlink”.
ut_orientation (None or Tensor of shape [3], tf.float) – Orientation of the UT. If set to None, [\(\pi\), 0, 0] is used. Defaults to None.
bs_orientation (None or Tensor of shape [3], tf.float) – Orientation of the BS. If set to None, [0, 0, 0] is used. Defaults to None.
min_speed (float) – Minimum speed [m/s]. Defaults to 0.
max_speed (None or float) – Maximum speed [m/s]. If set to None, then
max_speedtakes the same value asmin_speed. Defaults to None.dtype (Complex tf.DType) – Defines the datatype for internal calculations and the output dtype. Defaults to tf.complex64.
- Input:
batch_size (int) – Batch size
num_time_steps (int) – Number of time steps
sampling_frequency (float) – Sampling frequency [Hz]
- Output:
a ([batch size, num_rx = 1, num_rx_ant, num_tx = 1, num_tx_ant, num_paths, num_time_steps], tf.complex) – Path coefficients
tau ([batch size, num_rx = 1, num_tx = 1, num_paths], tf.float) – Path delays [s]
- property delay_spread
RMS delay spread [s]
- property delays
Path delays [s]
- property k_factor
K-factor in linear scale. Only available with LoS models.
- property los
True is this is a LoS model. False otherwise.
- property num_clusters
Number of paths (\(M\))
- property powers
Path powers in linear scale
Urban microcell (UMi)
- class sionna.channel.tr38901.UMi(carrier_frequency, o2i_model, ut_array, bs_array, direction, enable_pathloss=True, enable_shadow_fading=True, always_generate_lsp=False, dtype=tf.complex64)[source]
Urban microcell (UMi) channel model from 3GPP [TR38901] specification.
Setting up a UMi model requires configuring the network topology, i.e., the UTs and BSs locations, UTs velocities, etc. This is achieved using the
set_topology()method. Setting a different topology for each batch example is possible. The batch size used when setting up the network topology is used for the link simulations.The following code snippet shows how to setup a UMi channel model operating in the frequency domain:
>>> # UT and BS panel arrays >>> bs_array = PanelArray(num_rows_per_panel = 4, ... num_cols_per_panel = 4, ... polarization = 'dual', ... polarization_type = 'cross', ... antenna_pattern = '38.901', ... carrier_frequency = 3.5e9) >>> ut_array = PanelArray(num_rows_per_panel = 1, ... num_cols_per_panel = 1, ... polarization = 'single', ... polarization_type = 'V', ... antenna_pattern = 'omni', ... carrier_frequency = 3.5e9) >>> # Instantiating UMi channel model >>> channel_model = UMi(carrier_frequency = 3.5e9, ... o2i_model = 'low', ... ut_array = ut_array, ... bs_array = bs_array, ... direction = 'uplink') >>> # Setting up network topology >>> # ut_loc: UTs locations >>> # bs_loc: BSs locations >>> # ut_orientations: UTs array orientations >>> # bs_orientations: BSs array orientations >>> # in_state: Indoor/outdoor states of UTs >>> channel_model.set_topology(ut_loc, ... bs_loc, ... ut_orientations, ... bs_orientations, ... ut_velocities, ... in_state) >>> # Instanting the frequency domain channel >>> channel = OFDMChannel(channel_model = channel_model, ... resource_grid = rg)
where
rgis an instance ofResourceGrid.- Parameters:
carrier_frequency (float) – Carrier frequency in Hertz
o2i_model (str) – Outdoor-to-indoor loss model for UTs located indoor. Set this parameter to “low” to use the low-loss model, or to “high” to use the high-loss model. See section 7.4.3 of [TR38901] for details.
rx_array (PanelArray) – Panel array used by the receivers. All receivers share the same antenna array configuration.
tx_array (PanelArray) – Panel array used by the transmitters. All transmitters share the same antenna array configuration.
direction (str) – Link direction. Either “uplink” or “downlink”.
enable_pathloss (bool) – If True, apply pathloss. Otherwise doesn’t. Defaults to True.
enable_shadow_fading (bool) – If True, apply shadow fading. Otherwise doesn’t. Defaults to True.
always_generate_lsp (bool) – If True, new large scale parameters (LSPs) are generated for every new generation of channel impulse responses. Otherwise, always reuse the same LSPs, except if the topology is changed. Defaults to False.
dtype (Complex tf.DType) – Defines the datatype for internal calculations and the output dtype. Defaults to tf.complex64.
- Input:
num_time_steps (int) – Number of time steps
sampling_frequency (float) – Sampling frequency [Hz]
- Output:
a ([batch size, num_rx, num_rx_ant, num_tx, num_tx_ant, num_paths, num_time_steps], tf.complex) – Path coefficients
tau ([batch size, num_rx, num_tx, num_paths], tf.float) – Path delays [s]
- set_topology(ut_loc=None, bs_loc=None, ut_orientations=None, bs_orientations=None, ut_velocities=None, in_state=None, los=None)
Set the network topology.
It is possible to set up a different network topology for each batch example. The batch size used when setting up the network topology is used for the link simulations.
When calling this function, not specifying a parameter leads to the reuse of the previously given value. Not specifying a value that was not set at a former call rises an error.
- Input:
ut_loc ([batch size,num_ut, 3], tf.float) – Locations of the UTs
bs_loc ([batch size,num_bs, 3], tf.float) – Locations of BSs
ut_orientations ([batch size,num_ut, 3], tf.float) – Orientations of the UTs arrays [radian]
bs_orientations ([batch size,num_bs, 3], tf.float) – Orientations of the BSs arrays [radian]
ut_velocities ([batch size,num_ut, 3], tf.float) – Velocity vectors of UTs
in_state ([batch size,num_ut], tf.bool) – Indoor/outdoor state of UTs. True means indoor and False means outdoor.
los (tf.bool or None) – If not None (default value), all UTs located outdoor are forced to be in LoS if
losis set to True, or in NLoS if it is set to False. If set to None, the LoS/NLoS states of UTs is set following 3GPP specification [TR38901].
Note
If you want to use this function in Graph mode with XLA, i.e., within a function that is decorated with
@tf.function(jit_compile=True), you must setsionna.Config.xla_compat=true. Seexla_compat.
- show_topology(bs_index=0, batch_index=0)
Shows the network topology of the batch example with index
batch_index.The
bs_indexparameter specifies with respect to which BS the LoS/NLoS state of UTs is indicated.- Input:
bs_index (int) – BS index with respect to which the LoS/NLoS state of UTs is indicated. Defaults to 0.
batch_index (int) – Batch example for which the topology is shown. Defaults to 0.
Urban macrocell (UMa)
- class sionna.channel.tr38901.UMa(carrier_frequency, o2i_model, ut_array, bs_array, direction, enable_pathloss=True, enable_shadow_fading=True, always_generate_lsp=False, dtype=tf.complex64)[source]
Urban macrocell (UMa) channel model from 3GPP [TR38901] specification.
Setting up a UMa model requires configuring the network topology, i.e., the UTs and BSs locations, UTs velocities, etc. This is achieved using the
set_topology()method. Setting a different topology for each batch example is possible. The batch size used when setting up the network topology is used for the link simulations.The following code snippet shows how to setup an UMa channel model assuming an OFDM waveform:
>>> # UT and BS panel arrays >>> bs_array = PanelArray(num_rows_per_panel = 4, ... num_cols_per_panel = 4, ... polarization = 'dual', ... polarization_type = 'cross', ... antenna_pattern = '38.901', ... carrier_frequency = 3.5e9) >>> ut_array = PanelArray(num_rows_per_panel = 1, ... num_cols_per_panel = 1, ... polarization = 'single', ... polarization_type = 'V', ... antenna_pattern = 'omni', ... carrier_frequency = 3.5e9) >>> # Instantiating UMa channel model >>> channel_model = UMa(carrier_frequency = 3.5e9, ... o2i_model = 'low', ... ut_array = ut_array, ... bs_array = bs_array, ... direction = 'uplink') >>> # Setting up network topology >>> # ut_loc: UTs locations >>> # bs_loc: BSs locations >>> # ut_orientations: UTs array orientations >>> # bs_orientations: BSs array orientations >>> # in_state: Indoor/outdoor states of UTs >>> channel_model.set_topology(ut_loc, ... bs_loc, ... ut_orientations, ... bs_orientations, ... ut_velocities, ... in_state) >>> # Instanting the OFDM channel >>> channel = OFDMChannel(channel_model = channel_model, ... resource_grid = rg)
where
rgis an instance ofResourceGrid.- Parameters:
carrier_frequency (float) – Carrier frequency in Hertz
o2i_model (str) – Outdoor-to-indoor loss model for UTs located indoor. Set this parameter to “low” to use the low-loss model, or to “high” to use the high-loss model. See section 7.4.3 of [TR38901] for details.
rx_array (PanelArray) – Panel array used by the receivers. All receivers share the same antenna array configuration.
tx_array (PanelArray) – Panel array used by the transmitters. All transmitters share the same antenna array configuration.
direction (str) – Link direction. Either “uplink” or “downlink”.
enable_pathloss (bool) – If True, apply pathloss. Otherwise doesn’t. Defaults to True.
enable_shadow_fading (bool) – If True, apply shadow fading. Otherwise doesn’t. Defaults to True.
always_generate_lsp (bool) – If True, new large scale parameters (LSPs) are generated for every new generation of channel impulse responses. Otherwise, always reuse the same LSPs, except if the topology is changed. Defaults to False.
dtype (Complex tf.DType) – Defines the datatype for internal calculations and the output dtype. Defaults to tf.complex64.
- Input:
num_time_steps (int) – Number of time steps
sampling_frequency (float) – Sampling frequency [Hz]
- Output:
a ([batch size, num_rx, num_rx_ant, num_tx, num_tx_ant, num_paths, num_time_steps], tf.complex) – Path coefficients
tau ([batch size, num_rx, num_tx, num_paths], tf.float) – Path delays [s]
- set_topology(ut_loc=None, bs_loc=None, ut_orientations=None, bs_orientations=None, ut_velocities=None, in_state=None, los=None)
Set the network topology.
It is possible to set up a different network topology for each batch example. The batch size used when setting up the network topology is used for the link simulations.
When calling this function, not specifying a parameter leads to the reuse of the previously given value. Not specifying a value that was not set at a former call rises an error.
- Input:
ut_loc ([batch size,num_ut, 3], tf.float) – Locations of the UTs
bs_loc ([batch size,num_bs, 3], tf.float) – Locations of BSs
ut_orientations ([batch size,num_ut, 3], tf.float) – Orientations of the UTs arrays [radian]
bs_orientations ([batch size,num_bs, 3], tf.float) – Orientations of the BSs arrays [radian]
ut_velocities ([batch size,num_ut, 3], tf.float) – Velocity vectors of UTs
in_state ([batch size,num_ut], tf.bool) – Indoor/outdoor state of UTs. True means indoor and False means outdoor.
los (tf.bool or None) – If not None (default value), all UTs located outdoor are forced to be in LoS if
losis set to True, or in NLoS if it is set to False. If set to None, the LoS/NLoS states of UTs is set following 3GPP specification [TR38901].
Note
If you want to use this function in Graph mode with XLA, i.e., within a function that is decorated with
@tf.function(jit_compile=True), you must setsionna.Config.xla_compat=true. Seexla_compat.
- show_topology(bs_index=0, batch_index=0)
Shows the network topology of the batch example with index
batch_index.The
bs_indexparameter specifies with respect to which BS the LoS/NLoS state of UTs is indicated.- Input:
bs_index (int) – BS index with respect to which the LoS/NLoS state of UTs is indicated. Defaults to 0.
batch_index (int) – Batch example for which the topology is shown. Defaults to 0.
Rural macrocell (RMa)
- class sionna.channel.tr38901.RMa(carrier_frequency, ut_array, bs_array, direction, enable_pathloss=True, enable_shadow_fading=True, always_generate_lsp=False, dtype=tf.complex64)[source]
Rural macrocell (RMa) channel model from 3GPP [TR38901] specification.
Setting up a RMa model requires configuring the network topology, i.e., the UTs and BSs locations, UTs velocities, etc. This is achieved using the
set_topology()method. Setting a different topology for each batch example is possible. The batch size used when setting up the network topology is used for the link simulations.The following code snippet shows how to setup an RMa channel model assuming an OFDM waveform:
>>> # UT and BS panel arrays >>> bs_array = PanelArray(num_rows_per_panel = 4, ... num_cols_per_panel = 4, ... polarization = 'dual', ... polarization_type = 'cross', ... antenna_pattern = '38.901', ... carrier_frequency = 3.5e9) >>> ut_array = PanelArray(num_rows_per_panel = 1, ... num_cols_per_panel = 1, ... polarization = 'single', ... polarization_type = 'V', ... antenna_pattern = 'omni', ... carrier_frequency = 3.5e9) >>> # Instantiating RMa channel model >>> channel_model = RMa(carrier_frequency = 3.5e9, ... ut_array = ut_array, ... bs_array = bs_array, ... direction = 'uplink') >>> # Setting up network topology >>> # ut_loc: UTs locations >>> # bs_loc: BSs locations >>> # ut_orientations: UTs array orientations >>> # bs_orientations: BSs array orientations >>> # in_state: Indoor/outdoor states of UTs >>> channel_model.set_topology(ut_loc, ... bs_loc, ... ut_orientations, ... bs_orientations, ... ut_velocities, ... in_state) >>> # Instanting the OFDM channel >>> channel = OFDMChannel(channel_model = channel_model, ... resource_grid = rg)
where
rgis an instance ofResourceGrid.- Parameters:
carrier_frequency (float) – Carrier frequency [Hz]
rx_array (PanelArray) – Panel array used by the receivers. All receivers share the same antenna array configuration.
tx_array (PanelArray) – Panel array used by the transmitters. All transmitters share the same antenna array configuration.
direction (str) – Link direction. Either “uplink” or “downlink”.
enable_pathloss (bool) – If True, apply pathloss. Otherwise doesn’t. Defaults to True.
enable_shadow_fading (bool) – If True, apply shadow fading. Otherwise doesn’t. Defaults to True.
average_street_width (float) – Average street width [m]. Defaults to 5m.
average_street_width – Average building height [m]. Defaults to 20m.
always_generate_lsp (bool) – If True, new large scale parameters (LSPs) are generated for every new generation of channel impulse responses. Otherwise, always reuse the same LSPs, except if the topology is changed. Defaults to False.
dtype (Complex tf.DType) – Defines the datatype for internal calculations and the output dtype. Defaults to tf.complex64.
- Input:
num_time_steps (int) – Number of time steps
sampling_frequency (float) – Sampling frequency [Hz]
- Output:
a ([batch size, num_rx, num_rx_ant, num_tx, num_tx_ant, num_paths, num_time_steps], tf.complex) – Path coefficients
tau ([batch size, num_rx, num_tx, num_paths], tf.float) – Path delays [s]
- set_topology(ut_loc=None, bs_loc=None, ut_orientations=None, bs_orientations=None, ut_velocities=None, in_state=None, los=None)
Set the network topology.
It is possible to set up a different network topology for each batch example. The batch size used when setting up the network topology is used for the link simulations.
When calling this function, not specifying a parameter leads to the reuse of the previously given value. Not specifying a value that was not set at a former call rises an error.
- Input:
ut_loc ([batch size,num_ut, 3], tf.float) – Locations of the UTs
bs_loc ([batch size,num_bs, 3], tf.float) – Locations of BSs
ut_orientations ([batch size,num_ut, 3], tf.float) – Orientations of the UTs arrays [radian]
bs_orientations ([batch size,num_bs, 3], tf.float) – Orientations of the BSs arrays [radian]
ut_velocities ([batch size,num_ut, 3], tf.float) – Velocity vectors of UTs
in_state ([batch size,num_ut], tf.bool) – Indoor/outdoor state of UTs. True means indoor and False means outdoor.
los (tf.bool or None) – If not None (default value), all UTs located outdoor are forced to be in LoS if
losis set to True, or in NLoS if it is set to False. If set to None, the LoS/NLoS states of UTs is set following 3GPP specification [TR38901].
Note
If you want to use this function in Graph mode with XLA, i.e., within a function that is decorated with
@tf.function(jit_compile=True), you must setsionna.Config.xla_compat=true. Seexla_compat.
- show_topology(bs_index=0, batch_index=0)
Shows the network topology of the batch example with index
batch_index.The
bs_indexparameter specifies with respect to which BS the LoS/NLoS state of UTs is indicated.- Input:
bs_index (int) – BS index with respect to which the LoS/NLoS state of UTs is indicated. Defaults to 0.
batch_index (int) – Batch example for which the topology is shown. Defaults to 0.
External datasets
- class sionna.channel.CIRDataset(cir_generator, batch_size, num_rx, num_rx_ant, num_tx, num_tx_ant, num_paths, num_time_steps, dtype=tf.complex64)[source]
Creates a channel model from a dataset that can be used with classes such as
TimeChannelandOFDMChannel. The dataset is defined by a generator.The batch size is configured when instantiating the dataset or through the
batch_sizeproperty. The number of time steps (num_time_steps) and sampling frequency (sampling_frequency) can only be set when instantiating the dataset. The specified values must be in accordance with the data.Example
The following code snippet shows how to use this class as a channel model.
>>> my_generator = MyGenerator(...) >>> channel_model = sionna.channel.CIRDataset(my_generator, ... batch_size, ... num_rx, ... num_rx_ant, ... num_tx, ... num_tx_ant, ... num_paths, ... num_time_steps+l_tot-1) >>> channel = sionna.channel.TimeChannel(channel_model, bandwidth, num_time_steps)
where
MyGeneratoris a generator>>> class MyGenerator: ... ... def __call__(self): ... ... ... yield a, tau
that returns complex-valued path coefficients
awith shape [num_rx, num_rx_ant, num_tx, num_tx_ant, num_paths, num_time_steps] and real-valued path delaystau(in second) [num_rx, num_tx, num_paths].- Parameters:
cir_generator – Generator that returns channel impulse responses
(a, tau)whereais the tensor of channel coefficients of shape [num_rx, num_rx_ant, num_tx, num_tx_ant, num_paths, num_time_steps] and dtypedtype, andtauthe tensor of path delays of shape [num_rx, num_tx, num_paths] and dtypedtype. real_dtype.batch_size (int) – Batch size
num_rx (int) – Number of receivers (\(N_R\))
num_rx_ant (int) – Number of antennas per receiver (\(N_{RA}\))
num_tx (int) – Number of transmitters (\(N_T\))
num_tx_ant (int) – Number of antennas per transmitter (\(N_{TA}\))
num_paths (int) – Number of paths (\(M\))
num_time_steps (int) – Number of time steps
dtype (tf.DType) – Complex datatype to use for internal processing and output. Defaults to tf.complex64.
- Output:
a ([batch size, num_rx, num_rx_ant, num_tx, num_tx_ant, num_paths, num_time_steps], tf.complex) – Path coefficients
tau ([batch size, num_rx, num_tx, num_paths], tf.float) – Path delays [s]
- property batch_size
Batch size
Utility functions
subcarrier_frequencies
- sionna.channel.subcarrier_frequencies(num_subcarriers, subcarrier_spacing, dtype=tf.complex64)[source]
Compute the baseband frequencies of
num_subcarriersubcarriers spaced bysubcarrier_spacing, i.e.,>>> # If num_subcarrier is even: >>> frequencies = [-num_subcarrier/2, ..., 0, ..., num_subcarrier/2-1] * subcarrier_spacing >>> >>> # If num_subcarrier is odd: >>> frequencies = [-(num_subcarrier-1)/2, ..., 0, ..., (num_subcarrier-1)/2] * subcarrier_spacing
- Input:
num_subcarriers (int) – Number of subcarriers
subcarrier_spacing (float) – Subcarrier spacing [Hz]
dtype (tf.DType) – Datatype to use for internal processing and output. If a complex datatype is provided, the corresponding precision of real components is used. Defaults to tf.complex64 (tf.float32).
- Output:
frequencies ([
num_subcarrier], tf.float) – Baseband frequencies of subcarriers
time_lag_discrete_time_channel
- sionna.channel.time_lag_discrete_time_channel(bandwidth, maximum_delay_spread=3e-06)[source]
Compute the smallest and largest time-lag for the descrete complex baseband channel, i.e., \(L_{\text{min}}\) and \(L_{\text{max}}\).
The smallest time-lag (\(L_{\text{min}}\)) returned is always -6, as this value was found small enough for all models included in Sionna.
The largest time-lag (\(L_{\text{max}}\)) is computed from the
bandwidthandmaximum_delay_spreadas follows:\[L_{\text{max}} = \lceil W \tau_{\text{max}} \rceil + 6\]where \(L_{\text{max}}\) is the largest time-lag, \(W\) the
bandwidth, and \(\tau_{\text{max}}\) themaximum_delay_spread.The default value for the
maximum_delay_spreadis 3us, which was found to be large enough to include most significant paths with all channel models included in Sionna assuming a nominal delay spread of 100ns.Note
The values of \(L_{\text{min}}\) and \(L_{\text{max}}\) computed by this function are only recommended values. \(L_{\text{min}}\) and \(L_{\text{max}}\) should be set according to the considered channel model. For OFDM systems, one also needs to be careful that the effective length of the complex baseband channel is not larger than the cyclic prefix length.
- Input:
bandwidth (float) – Bandwith (\(W\)) [Hz]
maximum_delay_spread (float) – Maximum delay spread [s]. Defaults to 3us.
- Output:
l_min (int) – Smallest time-lag (\(L_{\text{min}}\)) for the descrete complex baseband channel. Set to -6, , as this value was found small enough for all models included in Sionna.
l_max (int) – Largest time-lag (\(L_{\text{max}}\)) for the descrete complex baseband channel
deg_2_rad
rad_2_deg
wrap_angle_0_360
drop_uts_in_sector
- sionna.channel.drop_uts_in_sector(batch_size, num_ut, min_bs_ut_dist, isd, bs_height=0.0, ut_height=0.0, dtype=tf.complex64)[source]
Uniformly sample UT locations from a sector
The sector from which UTs are sampled is shown in the following figure. The BS is assumed to be located at the origin (0,0) of the coordinate system.
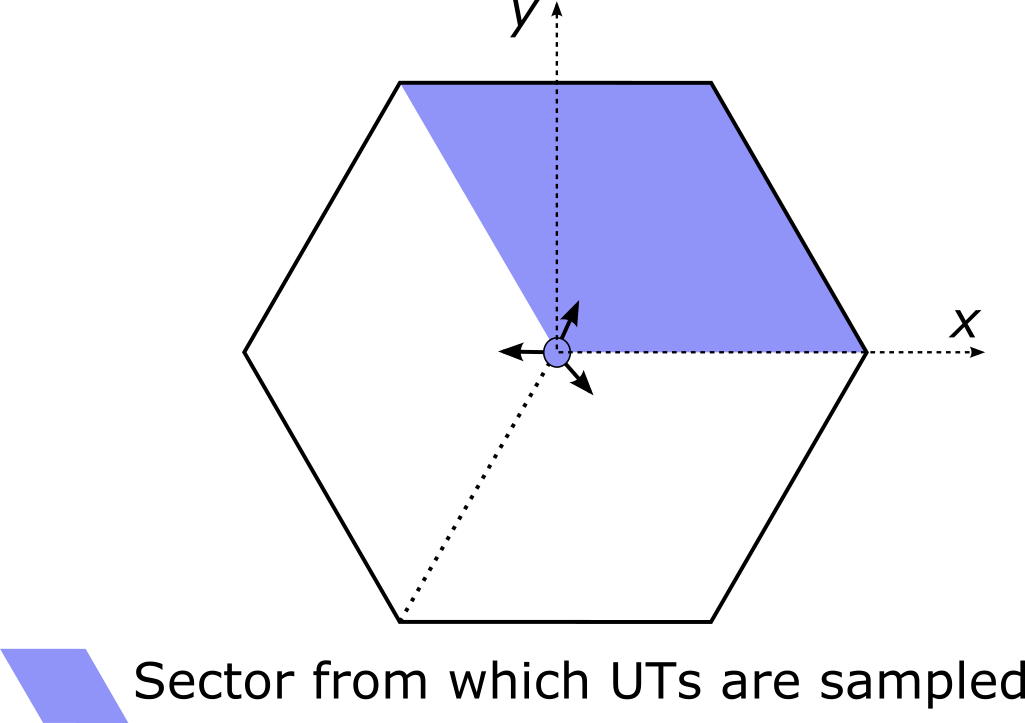
- Input:
batch_size (int) – Batch size
num_ut (int) – Number of UTs to sample per batch example
min_bs_ut_dist (tf.float) – Minimum BS-UT distance [m]
isd (tf.float) – Inter-site distance, i.e., the distance between two adjacent BSs [m]
bs_height (tf.float) – BS height, i.e., distance between the BS and the X-Y plane [m]. Defaults to 0.
ut_height (tf.float) – UT height, i.e., distance between the BS and the X-Y plane [m]. Defaults to 0.
dtype (tf.DType) – Datatype to use for internal processing and output. If a complex datatype is provided, the corresponding precision of real components is used. Defaults to tf.complex64 (tf.float32).
- Output:
ut_loc ([batch_size, num_ut, 2], tf.float) – UT locations in the X-Y plane
relocate_uts
- sionna.channel.relocate_uts(ut_loc, sector_id, cell_loc)[source]
Relocate the UTs by rotating them into the sector with index
sector_idand transposing them to the cell centered oncell_loc.sector_idgives the index of the sector to which the UTs are rotated to. The picture below shows how the three sectors of a cell are indexed.
Fig. 12 Indexing of sectors
If
sector_idis a scalar, then all UTs are relocated to the same sector indexed bysector_id. Ifsector_idis a tensor, it should be broadcastable with [batch_size,num_ut], and give the sector in which each UT or batch example is relocated to.When calling the function,
ut_locgives the locations of the UTs to relocate, which are all assumed to be in sector with index 0, and in the cell centered on the origin (0,0).- Input:
ut_loc ([batch_size, num_ut, 2], tf.float) – UTs locations in the X-Y plan
sector_id (Tensor broadcastable with [batch_size, num_ut], int) – Indexes of the sector to which to relocate the UTs
cell_loc (Tensor broadcastable with [batch_size, num_ut], tf.float) – Center of the cell to which to transpose the UTs
- Output:
ut_loc ([batch_size, num_ut, 2], tf.float) – Relocated UTs locations in the X-Y plan
set_3gpp_scenario_parameters
- sionna.channel.set_3gpp_scenario_parameters(scenario, min_bs_ut_dist=None, isd=None, bs_height=None, min_ut_height=None, max_ut_height=None, indoor_probability=None, min_ut_velocity=None, max_ut_velocity=None, dtype=tf.complex64)[source]
Set valid parameters for a specified 3GPP system level
scenario(RMa, UMi, or UMa).If a parameter is given, then it is returned. If it is set to None, then a parameter valid according to the chosen scenario is returned (see [TR38901]).
- Input:
scenario (str) – System level model scenario. Must be one of “rma”, “umi”, or “uma”.
min_bs_ut_dist (None or tf.float) – Minimum BS-UT distance [m]
isd (None or tf.float) – Inter-site distance [m]
bs_height (None or tf.float) – BS elevation [m]
min_ut_height (None or tf.float) – Minimum UT elevation [m]
max_ut_height (None or tf.float) – Maximum UT elevation [m]
indoor_probability (None or tf.float) – Probability of a UT to be indoor
min_ut_velocity (None or tf.float) – Minimum UT velocity [m/s]
max_ut_velocity (None or tf.float) – Maximim UT velocity [m/s]
dtype (tf.DType) – Datatype to use for internal processing and output. If a complex datatype is provided, the corresponding precision of real components is used. Defaults to tf.complex64 (tf.float32).
- Output:
min_bs_ut_dist (tf.float) – Minimum BS-UT distance [m]
isd (tf.float) – Inter-site distance [m]
bs_height (tf.float) – BS elevation [m]
min_ut_height (tf.float) – Minimum UT elevation [m]
max_ut_height (tf.float) – Maximum UT elevation [m]
indoor_probability (tf.float) – Probability of a UT to be indoor
min_ut_velocity (tf.float) – Minimum UT velocity [m/s]
max_ut_velocity (tf.float) – Maximim UT velocity [m/s]
gen_single_sector_topology
- sionna.channel.gen_single_sector_topology(batch_size, num_ut, scenario, min_bs_ut_dist=None, isd=None, bs_height=None, min_ut_height=None, max_ut_height=None, indoor_probability=None, min_ut_velocity=None, max_ut_velocity=None, dtype=tf.complex64)[source]
Generate a batch of topologies consisting of a single BS located at the origin and
num_utUTs randomly and uniformly dropped in a cell sector.The following picture shows the sector from which UTs are sampled.

UTs orientations are randomly and uniformly set, whereas the BS orientation is set such that the it is oriented towards the center of the sector.
The drop configuration can be controlled through the optional parameters. Parameters set to None are set to valid values according to the chosen
scenario(see [TR38901]).The returned batch of topologies can be used as-is with the
set_topology()method of the system level models, i.e.UMi,UMa, andRMa.Example
>>> # Create antenna arrays >>> bs_array = PanelArray(num_rows_per_panel = 4, ... num_cols_per_panel = 4, ... polarization = 'dual', ... polarization_type = 'VH', ... antenna_pattern = '38.901', ... carrier_frequency = 3.5e9) >>> >>> ut_array = PanelArray(num_rows_per_panel = 1, ... num_cols_per_panel = 1, ... polarization = 'single', ... polarization_type = 'V', ... antenna_pattern = 'omni', ... carrier_frequency = 3.5e9) >>> # Create channel model >>> channel_model = UMi(carrier_frequency = 3.5e9, ... o2i_model = 'low', ... ut_array = ut_array, ... bs_array = bs_array, ... direction = 'uplink') >>> # Generate the topology >>> topology = gen_single_sector_topology(batch_size = 100, ... num_ut = 4, ... scenario = 'umi') >>> # Set the topology >>> ut_loc, bs_loc, ut_orientations, bs_orientations, ut_velocities, in_state = topology >>> channel_model.set_topology(ut_loc, ... bs_loc, ... ut_orientations, ... bs_orientations, ... ut_velocities, ... in_state) >>> channel_model.show_topology()
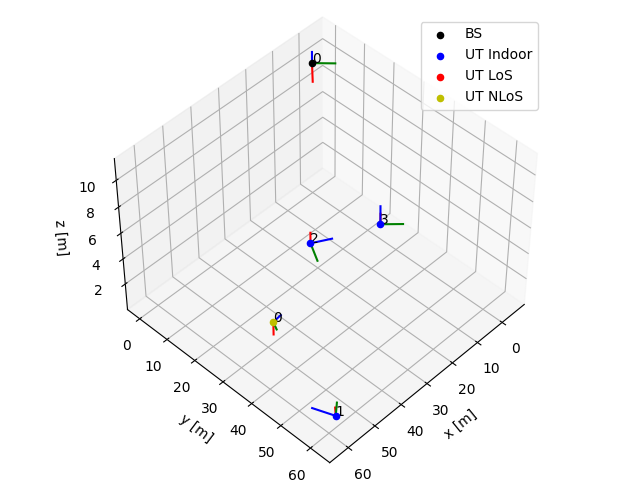
- Input:
batch_size (int) – Batch size
num_ut (int) – Number of UTs to sample per batch example
scenario (str) – System leven model scenario. Must be one of “rma”, “umi”, or “uma”.
min_bs_ut_dist (None or tf.float) – Minimum BS-UT distance [m]
isd (None or tf.float) – Inter-site distance [m]
bs_height (None or tf.float) – BS elevation [m]
min_ut_height (None or tf.float) – Minimum UT elevation [m]
max_ut_height (None or tf.float) – Maximum UT elevation [m]
indoor_probability (None or tf.float) – Probability of a UT to be indoor
min_ut_velocity (None or tf.float) – Minimum UT velocity [m/s]
max_ut_velocity (None or tf.float) – Maximim UT velocity [m/s]
dtype (tf.DType) – Datatype to use for internal processing and output. If a complex datatype is provided, the corresponding precision of real components is used. Defaults to tf.complex64 (tf.float32).
- Output:
ut_loc ([batch_size, num_ut, 3], tf.float) – UTs locations
bs_loc ([batch_size, 1, 3], tf.float) – BS location. Set to (0,0,0) for all batch examples.
ut_orientations ([batch_size, num_ut, 3], tf.float) – UTs orientations [radian]
bs_orientations ([batch_size, 1, 3], tf.float) – BS orientations [radian]. Oriented towards the center of the sector.
ut_velocities ([batch_size, num_ut, 3], tf.float) – UTs velocities [m/s]
in_state ([batch_size, num_ut], tf.float) – Indoor/outdoor state of UTs. True means indoor, False means outdoor.
gen_single_sector_topology_interferers
- sionna.channel.gen_single_sector_topology_interferers(batch_size, num_ut, num_interferer, scenario, min_bs_ut_dist=None, isd=None, bs_height=None, min_ut_height=None, max_ut_height=None, indoor_probability=None, min_ut_velocity=None, max_ut_velocity=None, dtype=tf.complex64)[source]
Generate a batch of topologies consisting of a single BS located at the origin,
num_utUTs randomly and uniformly dropped in a cell sector, andnum_interfererinterfering UTs randomly dropped in the adjacent cells.The following picture shows how UTs are sampled
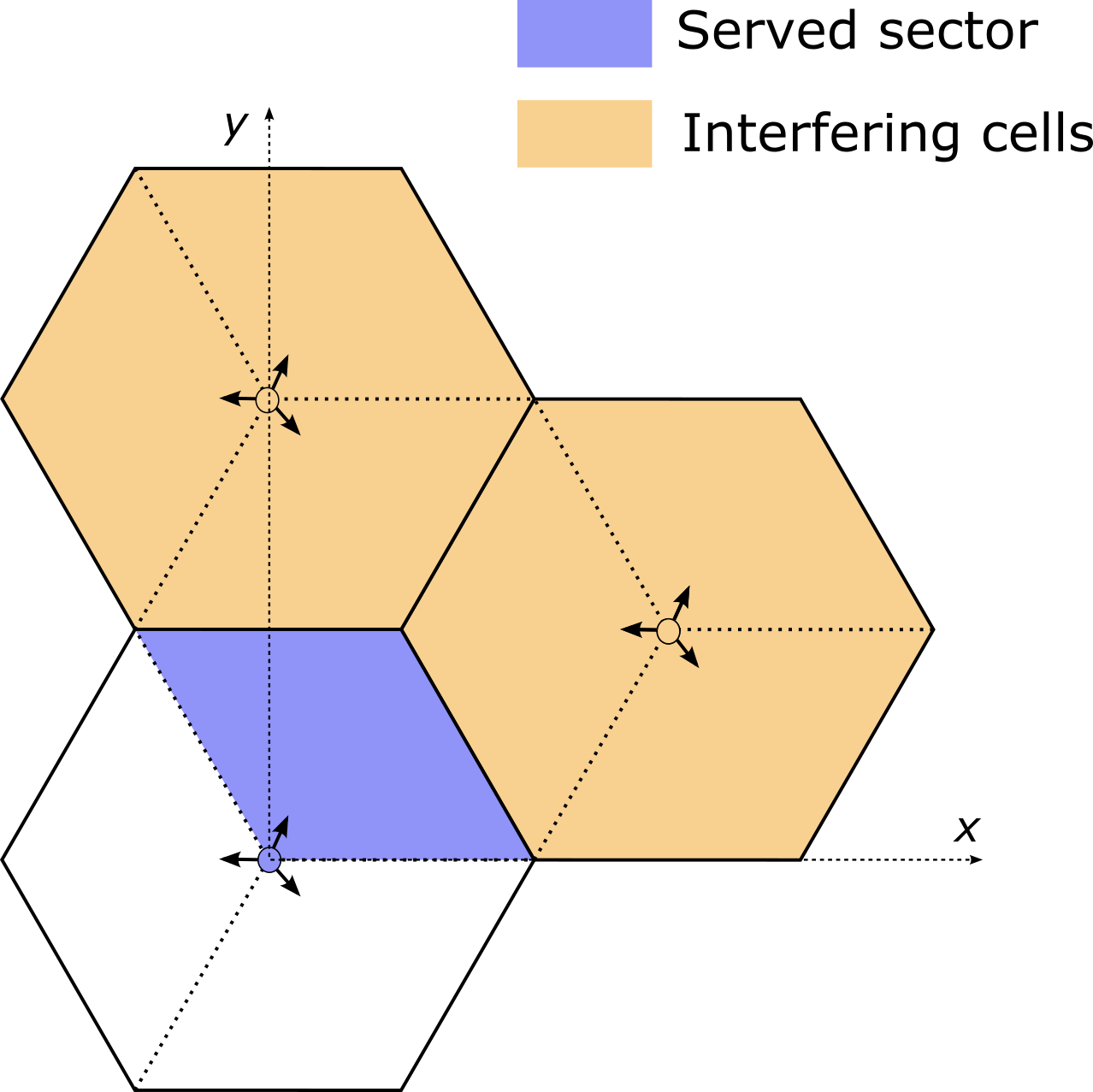
UTs orientations are randomly and uniformly set, whereas the BS orientation is set such that it is oriented towards the center of the sector it serves.
The drop configuration can be controlled through the optional parameters. Parameters set to None are set to valid values according to the chosen
scenario(see [TR38901]).The returned batch of topologies can be used as-is with the
set_topology()method of the system level models, i.e.UMi,UMa, andRMa.In the returned
ut_loc,ut_orientations,ut_velocities, andin_statetensors, the firstnum_utitems along the axis with index 1 correspond to the served UTs, whereas the remainingnum_interfereritems correspond to the interfering UTs.Example
>>> # Create antenna arrays >>> bs_array = PanelArray(num_rows_per_panel = 4, ... num_cols_per_panel = 4, ... polarization = 'dual', ... polarization_type = 'VH', ... antenna_pattern = '38.901', ... carrier_frequency = 3.5e9) >>> >>> ut_array = PanelArray(num_rows_per_panel = 1, ... num_cols_per_panel = 1, ... polarization = 'single', ... polarization_type = 'V', ... antenna_pattern = 'omni', ... carrier_frequency = 3.5e9) >>> # Create channel model >>> channel_model = UMi(carrier_frequency = 3.5e9, ... o2i_model = 'low', ... ut_array = ut_array, ... bs_array = bs_array, ... direction = 'uplink') >>> # Generate the topology >>> topology = gen_single_sector_topology_interferers(batch_size = 100, ... num_ut = 4, ... num_interferer = 4, ... scenario = 'umi') >>> # Set the topology >>> ut_loc, bs_loc, ut_orientations, bs_orientations, ut_velocities, in_state = topology >>> channel_model.set_topology(ut_loc, ... bs_loc, ... ut_orientations, ... bs_orientations, ... ut_velocities, ... in_state) >>> channel_model.show_topology()
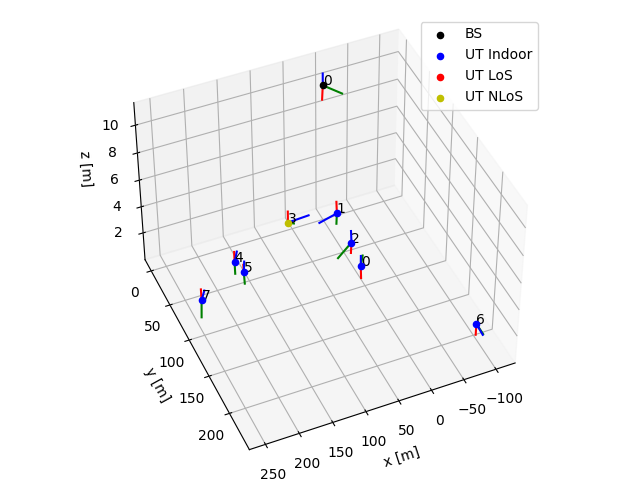
- Input:
batch_size (int) – Batch size
num_ut (int) – Number of UTs to sample per batch example
num_interferer (int) – Number of interfeering UTs per batch example
scenario (str) – System leven model scenario. Must be one of “rma”, “umi”, or “uma”.
min_bs_ut_dist (None or tf.float) – Minimum BS-UT distance [m]
isd (None or tf.float) – Inter-site distance [m]
bs_height (None or tf.float) – BS elevation [m]
min_ut_height (None or tf.float) – Minimum UT elevation [m]
max_ut_height (None or tf.float) – Maximum UT elevation [m]
indoor_probability (None or tf.float) – Probability of a UT to be indoor
min_ut_velocity (None or tf.float) – Minimum UT velocity [m/s]
max_ut_velocity (None or tf.float) – Maximim UT velocity [m/s]
dtype (tf.DType) – Datatype to use for internal processing and output. If a complex datatype is provided, the corresponding precision of real components is used. Defaults to tf.complex64 (tf.float32).
- Output:
ut_loc ([batch_size, num_ut, 3], tf.float) – UTs locations. The first
num_utitems along the axis with index 1 correspond to the served UTs, whereas the remainingnum_interfereritems correspond to the interfeering UTs.bs_loc ([batch_size, 1, 3], tf.float) – BS location. Set to (0,0,0) for all batch examples.
ut_orientations ([batch_size, num_ut, 3], tf.float) – UTs orientations [radian]. The first
num_utitems along the axis with index 1 correspond to the served UTs, whereas the remainingnum_interfereritems correspond to the interfeering UTs.bs_orientations ([batch_size, 1, 3], tf.float) – BS orientation [radian]. Oriented towards the center of the sector.
ut_velocities ([batch_size, num_ut, 3], tf.float) – UTs velocities [m/s]. The first
num_utitems along the axis with index 1 correspond to the served UTs, whereas the remainingnum_interfereritems correspond to the interfeering UTs.in_state ([batch_size, num_ut], tf.float) – Indoor/outdoor state of UTs. True means indoor, False means outdoor. The first
num_utitems along the axis with index 1 correspond to the served UTs, whereas the remainingnum_interfereritems correspond to the interfering UTs.
exp_corr_mat
- sionna.channel.exp_corr_mat(a, n, dtype=tf.complex64)[source]
Generate exponential correlation matrices.
This function computes for every element \(a\) of a complex-valued tensor \(\mathbf{a}\) the corresponding \(n\times n\) exponential correlation matrix \(\mathbf{R}(a,n)\), defined as (Eq. 1, [MAL2018]):
\[\begin{split}\mathbf{R}(a,n)_{i,j} = \begin{cases} 1 & \text{if } i=j\\ a^{i-j} & \text{if } i>j\\ (a^\star)^{j-i} & \text{if } j<i, j=1,\dots,n\\ \end{cases}\end{split}\]where \(|a|<1\) and \(\mathbf{R}\in\mathbb{C}^{n\times n}\).
- Input:
a ([n_0, …, n_k], tf.complex) – A tensor of arbitrary rank whose elements have an absolute value smaller than one.
n (int) – Number of dimensions of the output correlation matrices.
dtype (tf.complex64, tf.complex128) – The dtype of the output.
- Output:
R ([n_0, …, n_k, n, n], tf.complex) – A tensor of the same dtype as the input tensor \(\mathbf{a}\).
one_ring_corr_mat
- sionna.channel.one_ring_corr_mat(phi_deg, num_ant, d_h=0.5, sigma_phi_deg=15, dtype=tf.complex64)[source]
Generate covariance matrices from the one-ring model.
This function generates approximate covariance matrices for the so-called one-ring model (Eq. 2.24) [BHS2017]. A uniform linear array (ULA) with uniform antenna spacing is assumed. The elements of the covariance matrices are computed as:
\[\mathbf{R}_{\ell,m} = \exp\left( j2\pi d_\text{H} (\ell -m)\sin(\varphi) \right) \exp\left( -\frac{\sigma_\varphi^2}{2} \left( 2\pi d_\text{H}(\ell -m)\cos(\varphi) \right)^2 \right)\]for \(\ell,m = 1,\dots, M\), where \(M\) is the number of antennas, \(\varphi\) is the angle of arrival, \(d_\text{H}\) is the antenna spacing in multiples of the wavelength, and \(\sigma^2_\varphi\) is the angular standard deviation.
- Input:
phi_deg ([n_0, …, n_k], tf.float) – A tensor of arbitrary rank containing azimuth angles (deg) of arrival.
num_ant (int) – Number of antennas
d_h (float) – Antenna spacing in multiples of the wavelength. Defaults to 0.5.
sigma_phi_deg (float) – Angular standard deviation (deg). Defaults to 15 (deg). Values greater than 15 should not be used as the approximation becomes invalid.
dtype (tf.complex64, tf.complex128) – The dtype of the output.
- Output:
R ([n_0, …, n_k, num_ant, nun_ant], dtype) – Tensor containing the covariance matrices of the desired dtype.
- References:
- [TR38901] (1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17,18,19,20,21)
3GPP TR 38.901, “Study on channel model for frequencies from 0.5 to 100 GHz”, Release 16.1
[TS38141-1]3GPP TS 38.141-1 “Base Station (BS) conformance testing Part 1: Conducted conformance testing”, Release 17
[Tse]D. Tse and P. Viswanath, “Fundamentals of wireless communication“, Cambridge University Press, 2005.
[SoS]C. Xiao, Y. R. Zheng and N. C. Beaulieu, “Novel Sum-of-Sinusoids Simulation Models for Rayleigh and Rician Fading Channels,” in IEEE Transactions on Wireless Communications, vol. 5, no. 12, pp. 3667-3679, December 2006, doi: 10.1109/TWC.2006.256990.
[MAL2018]R. K. Mallik, “The exponential correlation matrix: Eigen-analysis and applications”, IEEE Trans. Wireless Commun., vol. 17, no. 7, pp. 4690-4705, Jul. 2018.
[BHS2017]E. Björnson, J. Hoydis, L. Sanguinetti (2017), “Massive MIMO Networks: Spectral, Energy, and Hardware Efficiency”, Foundations and Trends in Signal Processing: Vol. 11, No. 3-4, pp 154–655.