Discrete Channel Models
This module provides layers and functions that implement channel models with discrete input/output alphabets.
All channel models support binary inputs \(x \in \{0, 1\}\) and bipolar inputs \(x \in \{-1, 1\}\), respectively. In the later case, it is assumed that each 0 is mapped to -1.
The channels can either return discrete values or log-likelihood ratios (LLRs). These LLRs describe the channel transition probabilities \(L(y|X=1)=L(X=1|y)+L_a(X=1)\) where \(L_a(X=1)=\operatorname{log} \frac{P(X=1)}{P(X=0)}\) depends only on the a priori probability of \(X=1\). These LLRs equal the a posteriori probability if \(P(X=1)=P(X=0)=0.5\).
Further, the channel reliability parameter \(p_b\) can be either a scalar value or a tensor of any shape that can be broadcasted to the input. This allows for the efficient implementation of channels with non-uniform error probabilities.
The channel models are based on the Gumble-softmax trick [GumbleSoftmax] to ensure differentiability of the channel w.r.t. to the channel reliability parameter. Please see [LearningShaping] for further details.
Setting-up:
>>> bsc = BinarySymmetricChannel(return_llrs=False, bipolar_input=False)
Running:
>>> x = tf.zeros((128,)) # x is the channel input
>>> pb = 0.1 # pb is the bit flipping probability
>>> y = bsc((x, pb))
- class sionna.phy.channel.BinaryErasureChannel(return_llrs=False, bipolar_input=False, llr_max=100.0, precision=None, **kwargs)[source]
Binary erasure channel (BEC) where a bit is either correctly received or erased.
In the binary erasure channel, bits are always correctly received or erased with erasure probability \(p_\text{b}\).
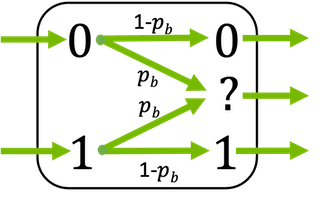
This block supports binary inputs (\(x \in \{0, 1\}\)) and bipolar inputs (\(x \in \{-1, 1\}\)).
If activated, the channel directly returns log-likelihood ratios (LLRs) defined as
\[\begin{split}\ell = \begin{cases} -\infty, \qquad \text{if} \, y=0 \\ 0, \qquad \quad \,\, \text{if} \, y=? \\ \infty, \qquad \quad \text{if} \, y=1 \\ \end{cases}\end{split}\]The erasure probability \(p_\text{b}\) can be either a scalar or a tensor (broadcastable to the shape of the input). This allows different erasure probabilities per bit position.
Please note that the output of the BEC is ternary. Hereby, -1 indicates an erasure for the binary configuration and 0 for the bipolar mode, respectively.
- Parameters:
return_llrs (bool, (default False)) – If True, the layer returns log-likelihood ratios instead of binary values based on
pb.bipolar_input (bool, (default False)) – If True, the expected input is given as \(\{-1,1\}\) instead of \(\{0,1\}\).
llr_max (tf.float, (default 100)) – Clipping value of the LLRs
precision (None (default) | “single” | “double”) – Precision used for internal calculations and outputs. If set to None,
precisionis used.
- Input:
x ([…,n], tf.float) – Input sequence to the channel
pb (tf.float) – Erasure probability. Can be a scalar or of any shape that can be broadcasted to the shape of
x.
- Output:
[…,n], tf.float – Output sequence of same length as the input
x. Ifreturn_llrsis False, the output is ternary where each -1 and each 0 indicate an erasure for the binary and bipolar input, respectively.
- class sionna.phy.channel.BinaryMemorylessChannel(return_llrs=False, bipolar_input=False, llr_max=100.0, precision=None, **kwargs)[source]
Discrete binary memory less channel with (possibly) asymmetric bit flipping probabilities
Inputs bits are flipped with probability \(p_\text{b,0}\) and \(p_\text{b,1}\), respectively.
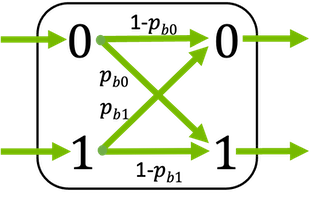
This block supports binary inputs (\(x \in \{0, 1\}\)) and bipolar inputs (\(x \in \{-1, 1\}\)).
If activated, the channel directly returns log-likelihood ratios (LLRs) defined as
\[\begin{split}\ell = \begin{cases} \operatorname{log} \frac{p_{b,1}}{1-p_{b,0}}, \qquad \text{if} \, y=0 \\ \operatorname{log} \frac{1-p_{b,1}}{p_{b,0}}, \qquad \text{if} \, y=1 \\ \end{cases}\end{split}\]The error probability \(p_\text{b}\) can be either scalar or a tensor (broadcastable to the shape of the input). This allows different erasure probabilities per bit position. In any case, its last dimension must be of length 2 and is interpreted as \(p_\text{b,0}\) and \(p_\text{b,1}\).
- Parameters:
return_llrs (bool, (default False)) – If True, the layer returns log-likelihood ratios instead of binary values based on
pb.bipolar_input (bool, (default False)) – If True, the expected input is given as \(\{-1,1\}\) instead of \(\{0,1\}\).
llr_max (tf.float, (default 100)) – Clipping value of the LLRs
precision (None (default) | “single” | “double”) – Precision used for internal calculations and outputs. If set to None,
precisionis used.
- Input:
x ([…,n], tf.float32) – Input sequence to the channel consisting of binary values \(\{0,1\} ` or :math:\){-1,1}`, respectively
pb ([…,2], tf.float32) – Error probability. Can be a tuple of two scalars or of any shape that can be broadcasted to the shape of
x. It has an additional last dimension which is interpreted as \(p_\text{b,0}\) and \(p_\text{b,1}\).
- Output:
[…,n], tf.float32 – Output sequence of same length as the input
x. Ifreturn_llrsis False, the output is ternary where a -1 and 0 indicate an erasure for the binary and bipolar input, respectively.
- property llr_max
Get/set maximum value used for LLR calculations
- Type:
tf.float
- property temperature
Get/set temperature for Gumble-softmax trick
- Type:
tf.float32
- class sionna.phy.channel.BinarySymmetricChannel(return_llrs=False, bipolar_input=False, llr_max=100.0, precision=None, **kwargs)[source]
Discrete binary symmetric channel which randomly flips bits with probability \(p_\text{b}\)
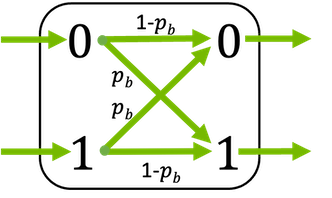
This layer supports binary inputs (\(x \in \{0, 1\}\)) and bipolar inputs (\(x \in \{-1, 1\}\)).
If activated, the channel directly returns log-likelihood ratios (LLRs) defined as
\[\begin{split}\ell = \begin{cases} \operatorname{log} \frac{p_{b}}{1-p_{b}}, \qquad \text{if}\, y=0 \\ \operatorname{log} \frac{1-p_{b}}{p_{b}}, \qquad \text{if}\, y=1 \\ \end{cases}\end{split}\]where \(y\) denotes the binary output of the channel.
The bit flipping probability \(p_\text{b}\) can be either a scalar or a tensor (broadcastable to the shape of the input). This allows different bit flipping probabilities per bit position.
- Parameters:
return_llrs (bool, (default False)) – If True, the layer returns log-likelihood ratios instead of binary values based on
pb.bipolar_input (bool, (default False)) – If True, the expected input is given as \(\{-1,1\}\) instead of \(\{0,1\}\).
llr_max (tf.float, (default 100)) – Clipping value of the LLRs
precision (None (default) | “single” | “double”) – Precision used for internal calculations and outputs. If set to None,
precisionis used.
- Input:
x ([…,n], tf.float32) – Input sequence to the channel
pb ([…,2], tf.float32) – Bit flipping probability. Can be a scalar or of any shape that can be broadcasted to the shape of
x.
- Output:
[…,n], tf.float32 – Output sequence of same length as the input
x. Ifreturn_llrsis False, the output is ternary where a -1 and 0 indicate an erasure for the binary and bipolar input, respectively.
- class sionna.phy.channel.BinaryZChannel(return_llrs=False, bipolar_input=False, llr_max=100.0, precision=None, **kwargs)[source]
Block that implements the binary Z-channel
In the Z-channel, transmission errors only occur for the transmission of second input element (i.e., if a 1 is transmitted) with error probability probability \(p_\text{b}\) but the first element is always correctly received.
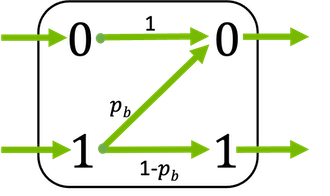
This block supports binary inputs (\(x \in \{0, 1\}\)) and bipolar inputs (\(x \in \{-1, 1\}\)).
If activated, the channel directly returns log-likelihood ratios (LLRs) defined as
\[\begin{split}\ell = \begin{cases} \operatorname{log} \left( p_b \right), \qquad \text{if} \, y=0 \\ \infty, \qquad \qquad \text{if} \, y=1 \\ \end{cases}\end{split}\]assuming equal probable inputs \(P(X=0) = P(X=1) = 0.5\).
The error probability \(p_\text{b}\) can be either a scalar or a tensor (broadcastable to the shape of the input). This allows different error probabilities per bit position.
- Parameters:
return_llrs (bool, (default False)) – If True, the layer returns log-likelihood ratios instead of binary values based on
pb.bipolar_input (bool, (default False)) – If True, the expected input is given as \(\{-1,1\}\) instead of \(\{0,1\}\).
llr_max (tf.float, (default 100)) – Clipping value of the LLRs
precision (None (default) | “single” | “double”) – Precision used for internal calculations and outputs. If set to None,
precisionis used.
- Input:
x ([…,n], tf.float32) – Input sequence to the channel
pb (tf.float32) – Error probability. Can be a scalar or of any shape that can be broadcasted to the shape of
x.
- Output:
[…,n], tf.float32 – Output sequence of same length as the input
x. Ifreturn_llrsis False, the output is binary and otherwise soft-values are returned.
- References:
- [GumbleSoftmax]
E. Jang, G. Shixiang, and B. Poole. “Categorical reparameterization with gumbel-softmax,” arXiv preprint arXiv:1611.01144 (2016).
[LearningShaping]M. Stark, F. Ait Aoudia, and J. Hoydis. “Joint learning of geometric and probabilistic constellation shaping,” 2019 IEEE Globecom Workshops (GC Wkshps). IEEE, 2019.