Polar Codes
The Polar code module supports 5G-compliant Polar codes and includes successive cancellation (SC), successive cancellation list (SCL), and belief propagation (BP) decoding.
The module supports rate-matching and CRC-aided decoding. Further, Reed-Muller (RM) code design is available and can be used in combination with the Polar encoding/decoding algorithms.
The following code snippets show how to setup and run a rate-matched 5G compliant Polar encoder and a corresponding successive cancellation list (SCL) decoder.
First, we need to create instances of Polar5GEncoder and Polar5GDecoder:
encoder = Polar5GEncoder(k = 100, # number of information bits (input)
n = 200) # number of codeword bits (output)
decoder = Polar5GDecoder(encoder = encoder, # connect the Polar decoder to the encoder
dec_type = "SCL", # can be also "SC" or "BP"
list_size = 8)
Now, the encoder and decoder can be used by:
# --- encoder ---
# u contains the information bits to be encoded and has shape [...,k].
# c contains the polar encoded codewords and has shape [...,n].
c = encoder(u)
# --- decoder ---
# llr contains the log-likelihood ratios from the demapper and has shape [...,n].
# u_hat contains the estimated information bits and has shape [...,k].
u_hat = decoder(llr)
- class sionna.phy.fec.polar.encoding.Polar5GEncoder(k, n, channel_type='uplink', verbose=False, precision=None, **kwargs)[source]
5G compliant Polar encoder including rate-matching following [3GPPTS38212] for the uplink scenario (UCI) and downlink scenario (DCI).
This block performs polar encoding for
kinformation bits and rate-matching such that the codeword lengths isn. This includes the CRC concatenation and the interleaving as defined in [3GPPTS38212].Note: block segmentation is currently not supported (I_seq=False).
We follow the basic structure from Fig. 6 in [Bioglio_Design].
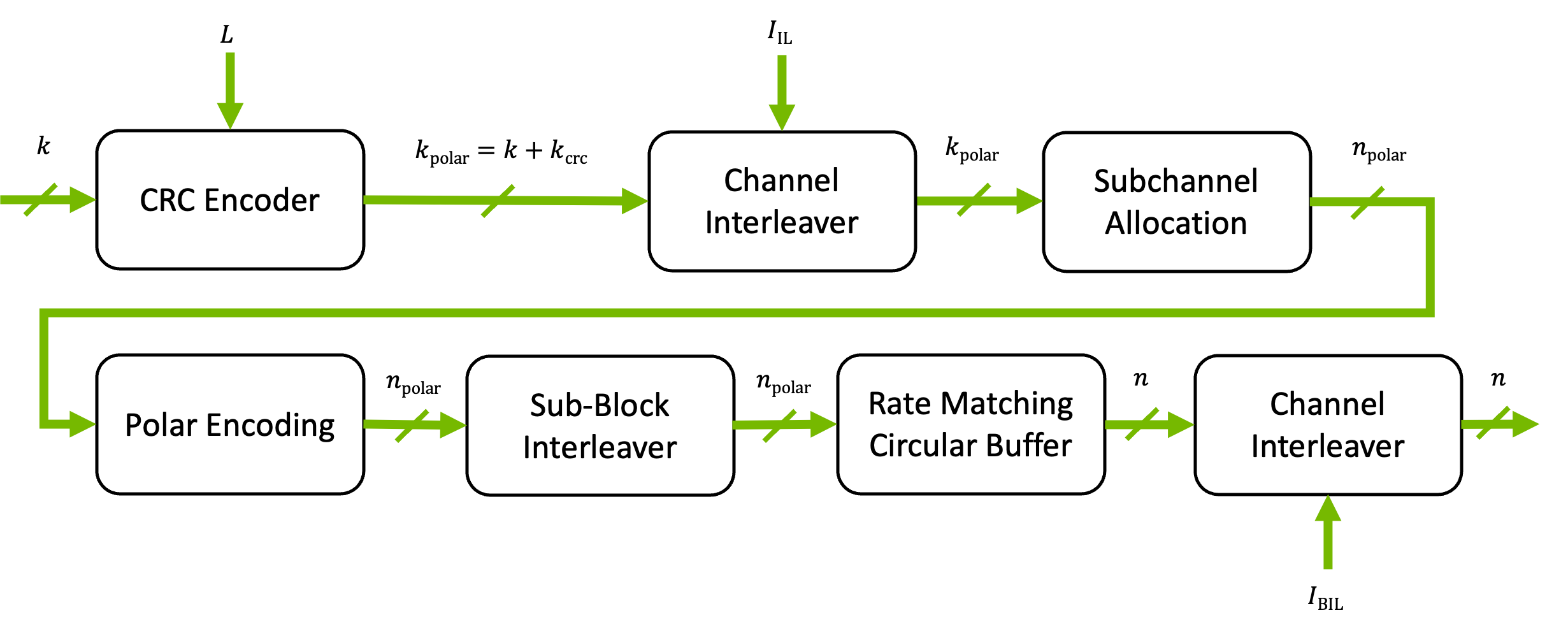
Fig. 11 Fig. 1: Implemented 5G Polar encoding chain following Fig. 6 in [Bioglio_Design] for the uplink (I_BIL = True) and the downlink (I_IL = True) scenario without block segmentation.
For further details, we refer to [3GPPTS38212], [Bioglio_Design] and [Hui_ChannelCoding].
- Parameters:
k (int) – Defining the number of information bit per codeword.
n (int) – Defining the codeword length.
channel_type ('uplink' (default) | 'downlink') – Can be ‘uplink’ or ‘downlink’.
verbose (bool, (default False)) – If True, rate-matching parameters will be printed.
precision (None (default) | ‘single’ | ‘double’) – Precision used for internal calculations and outputs. If set to None,
precisionis used.
- Input:
bits ([…,k], tf.float) – Binary tensor containing the information bits to be encoded.
- Output:
[…,n], tf.float – Binary tensor containing the codeword bits.
Note
The encoder supports the uplink Polar coding (UCI) scheme from [3GPPTS38212] and the downlink Polar coding (DCI) [3GPPTS38212], respectively.
For 12 <= k <= 19 the 3 additional parity bits as defined in [3GPPTS38212] are not implemented as it would also require a modified decoding procedure to materialize the potential gains.
Code segmentation is currently not supported and, thus,
nis limited to a maximum length of 1088 codeword bits.For the downlink scenario, the input length is limited to k <= 140 information bits due to the limited input bit interleaver size [3GPPTS38212].
For simplicity, the implementation does not exactly re-implement the DCI scheme from [3GPPTS38212]. This implementation neglects the all-one initialization of the CRC shift register and the scrambling of the CRC parity bits with the RNTI.
- channel_interleaver(c)[source]
Triangular interleaver following Sec. 5.4.1.3 in [3GPPTS38212].
- Input:
c (ndarray) – 1D array to be interleaved.
- Output:
ndarray – Interleaved version of
cwith same shape and dtype asc.
- property enc_crc
CRC encoder block used for CRC concatenation
- input_interleaver(c)[source]
Input interleaver following Sec. 5.4.1.1 in [3GPPTS38212].
- Input:
c (ndarray) – 1D array to be interleaved.
- Output:
ndarray – Interleaved version of
cwith same shape and dtype asc.
- property k
Number of information bits including rate-matching
- property k_polar
Number of information bits of the underlying Polar code
- property k_target
Number of information bits including rate-matching
- property n
Codeword length including rate-matching
- property n_polar
Codeword length of the underlying Polar code
- property n_target
Codeword length including rate-matching
- subblock_interleaving(u)[source]
Input bit interleaving as defined in Sec 5.4.1.1 [3GPPTS38212].
- Input:
u (ndarray) – 1D array to be interleaved. Length of
umust be a multiple of 32.- Output:
ndarray – Interleaved version of
uwith same shape and dtype asu.
- class sionna.phy.fec.polar.encoding.PolarEncoder(frozen_pos, n, precision=None, **kwargs)[source]
Polar encoder for given code parameters.
This block performs polar encoding for the given
kinformation bits and the frozen set (i.e., indices of frozen positions) specified byfrozen_pos.- Parameters:
frozen_pos (ndarray) – Array of int defining the n-k frozen indices, i.e., information bits are mapped onto the k complementary positions.
n (int) – Defining the codeword length.
precision (None (default) | ‘single’ | ‘double’) – Precision used for internal calculations and outputs. If set to None,
precisionis used.
- Input:
bits ([…,k], tf.float) – Binary tensor containing the information bits to be encoded.
- Output:
[…,n], tf.float – Binary tensor containing the codeword bits.
Note
As commonly done, we assume frozen bits are set to 0. Please note that - although its practical relevance is only little - setting frozen bits to 1 may result in affine codes instead of linear code as the all-zero codeword is not necessarily part of the code any more.
- property frozen_pos
Frozen positions for Polar decoding
- property info_pos
Information bit positions for Polar encoding
- property k
Number of information bits
- property n
Codeword length
- class sionna.phy.fec.polar.decoding.Polar5GDecoder(enc_polar, dec_type='SC', list_size=8, num_iter=20, return_crc_status=False, precision=None, **kwargs)[source]
Wrapper for 5G compliant decoding including rate-recovery and CRC removal.
- Parameters:
enc_polar (Polar5GEncoder) – Instance of the
Polar5GEncoderused for encoding including rate-matching.dec_type ("SC" (default) | "SCL" | "hybSCL" | "BP") – Defining the decoder to be used. Must be one of the following {“SC”, “SCL”, “hybSCL”, “BP”}.
list_size (int, (default 8)) – Defining the list size iff list-decoding is used. Only required for
dec_types{“SCL”, “hybSCL”}.num_iter (int, (default 20)) – Defining the number of BP iterations. Only required for
dec_type“BP”.return_crc_status (bool, (default False)) – If True, the decoder additionally returns the CRC status indicating if a codeword was (most likely) correctly recovered.
precision (None (default) | ‘single’ | ‘double’) – Precision used for internal calculations and outputs. If set to None,
precisionis used.
- Input:
llr_ch ([…,n], tf.float) – Tensor containing the channel logits/llr values.
- Output:
b_hat ([…,k], tf.float) – Binary tensor containing hard-decided estimations of all k information bits.
crc_status ([…], tf.bool) – CRC status indicating if a codeword was (most likely) correctly recovered. This is only returned if
return_crc_statusis True. Note that false positives are possible.
Note
This block supports the uplink and downlink Polar rate-matching scheme without codeword segmentation.
Although the decoding list size is not provided by 3GPP [3GPPTS38212], the consortium has agreed on a list size of 8 for the 5G decoding reference curves [Bioglio_Design].
All list-decoders apply CRC-aided decoding, however, the non-list decoders (“SC” and “BP”) cannot materialize the CRC leading to an effective rate-loss.
- property dec_type
Decoder type used for decoding as str
- property frozen_pos
Frozen positions for Polar decoding
- property info_pos
Information bit positions for Polar encoding
- property k_polar
Number of information bits of mother Polar code
- property k_target
Number of information bits including rate-matching
- property llr_max
Maximum LLR value for internal calculations
- property n_polar
Codeword length of mother Polar code
- property n_target
Codeword length including rate-matching
- property polar_dec
Decoder instance used for decoding
- class sionna.phy.fec.polar.decoding.PolarSCDecoder(frozen_pos, n, precision=None, **kwargs)[source]
Successive cancellation (SC) decoder [Arikan_Polar] for Polar codes and Polar-like codes.
- Parameters:
frozen_pos (ndarray) – Array of int defining the
n-kindices of the frozen positions.n (int) – Defining the codeword length.
precision (None (default) | ‘single’ | ‘double’) – Precision used for internal calculations and outputs. If set to None,
precisionis used.
- Input:
llr_ch ([…,n], tf.float) – Tensor containing the channel LLR values (as logits).
- Output:
[…,k], tf.float – Tensor containing hard-decided estimations of all
kinformation bits.
Note
This block implements the SC decoder as described in [Arikan_Polar]. However, the implementation follows the recursive tree [Gross_Fast_SCL] terminology and combines nodes for increased throughputs without changing the outcome of the algorithm.
As commonly done, we assume frozen bits are set to 0. Please note that - although its practical relevance is only little - setting frozen bits to 1 may result in affine codes instead of linear code as the all-zero codeword is not necessarily part of the code any more.
- property frozen_pos
Frozen positions for Polar decoding
- property info_pos
Information bit positions for Polar encoding
- property k
Number of information bits
- property llr_max
Maximum LLR value for internal calculations
- property n
Codeword length
- class sionna.phy.fec.polar.decoding.PolarSCLDecoder(frozen_pos, n, list_size=8, crc_degree=None, use_hybrid_sc=False, use_fast_scl=True, cpu_only=False, use_scatter=False, ind_iil_inv=None, return_crc_status=False, precision=None, **kwargs)[source]
Successive cancellation list (SCL) decoder [Tal_SCL] for Polar codes and Polar-like codes.
- Parameters:
frozen_pos (ndarray) – Array of int defining the
n-kindices of the frozen positions.n (int) – Defining the codeword length.
list_size (int, (default 8)) – Defines the list size of the decoder.
crc_degree (str, "CRC24A" | "CRC24B" | "CRC24C" | "CRC16" | "CRC11" | "CRC6") – Defining the CRC polynomial to be used. Can be any value from {CRC24A, CRC24B, CRC24C, CRC16, CRC11, CRC6}.
use_hybrid_sc (bool, (default False)) – If True, SC decoding is applied and only the codewords with invalid CRC are decoded with SCL. This option requires an outer CRC specified via
crc_degree. Remark: hybrid_sc does not support XLA optimization, i.e., @tf.function(jit_compile=True).use_fast_scl (bool, (default True)) – If True, Tree pruning is used to reduce the decoding complexity. The output is equivalent to the non-pruned version (besides numerical differences).
cpu_only (bool, (default False)) – If True, tf.py_function embedding is used and the decoder runs on the CPU. This option is usually slower, but also more memory efficient and in particular, recommended for larger blocklengths. Remark: cpu_only does not support XLA optimization @tf.function(jit_compile=True).
use_scatter (bool, (default False)) – If True, tf.tensor_scatter_update is used for tensor updates. This option is usually slower, but more memory efficient.
ind_iil_inv (None or [k+k_crc], int or tf.int) – Defaults to None. If not None, the sequence is used as inverse input bit interleaver before evaluating the CRC. Remark: this only effects the CRC evaluation but the output sequence is not permuted.
return_crc_status (bool, (default False)) – If True, the decoder additionally returns the CRC status indicating if a codeword was (most likely) correctly recovered. This is only available if
crc_degreeis not None.precision (None (default) | ‘single’ | ‘double’) – Precision used for internal calculations and outputs. If set to None,
precisionis used.
- Input:
llr_ch ([…,n], tf.float) – Tensor containing the channel LLR values (as logits).
- Output:
b_hat ([…,k], tf.float) – Binary tensor containing hard-decided estimations of all k information bits.
crc_status ([…], tf.bool) – CRC status indicating if a codeword was (most likely) correctly recovered. This is only returned if
return_crc_statusis True. Note that false positives are possible.
Note
This block implements the successive cancellation list (SCL) decoder as described in [Tal_SCL] but uses LLR-based message updates [Stimming_LLR]. The implementation follows the notation from [Gross_Fast_SCL], [Hashemi_SSCL]. If option use_fast_scl is active tree pruning is used and tree nodes are combined if possible (see [Hashemi_SSCL] for details).
Implementing SCL decoding as TensorFlow graph is a difficult task that requires several design tradeoffs to match the TF constraints while maintaining a reasonable throughput. Thus, the decoder minimizes the control flow as much as possible, leading to a strong memory occupation (e.g., due to full path duplication after each decision). For longer code lengths, the complexity of the decoding graph becomes large and we recommend to use the CPU_only option that uses an embedded Numpy decoder. Further, this function recursively unrolls the SCL decoding tree, thus, for larger values of
nbuilding the decoding graph can become time consuming. Please consider thecpu_onlyoption if building the graph takes to long.A hybrid SC/SCL decoder as proposed in [Cammerer_Hybrid_SCL] (using SC instead of BP) can be activated with option
use_hybrid_sciff an outer CRC is available. Please note that the results are not exactly SCL performance caused by the false positive rate of the CRC.As commonly done, we assume frozen bits are set to 0. Please note that - although its practical relevance is only little - setting frozen bits to 1 may result in affine codes instead of linear code as the all-zero codeword is not necessarily part of the code any more.
- property frozen_pos
Frozen positions for Polar decoding
- property info_pos
Information bit positions for Polar encoding
- property k
Number of information bits
- property k_crc
Number of CRC bits
- property list_size
List size for SCL decoding
- property llr_max
Maximum LLR value for internal calculations
- property n
Codeword length
- class sionna.phy.fec.polar.decoding.PolarBPDecoder(frozen_pos, n, num_iter=20, hard_out=True, precision=None, **kwargs)[source]
Belief propagation (BP) decoder for Polar codes [Arikan_Polar] and Polar-like codes based on [Arikan_BP] and [Forney_Graphs].
Remark: The PolarBPDecoder does currently not support XLA.
- Parameters:
frozen_pos (ndarray) – Array of int defining the
n-kindices of the frozen positions.n (int) – Defining the codeword length.
num_iter (int) – Defining the number of decoder iterations (no early stopping used at the moment).
hard_out (bool, (default True)) – If True, the decoder provides hard-decided information bits instead of soft-values.
precision (None (default) | ‘single’ | ‘double’) – Precision used for internal calculations and outputs. If set to None,
precisionis used.
- Input:
llr_ch ([…,n], tf.float32) – Tensor containing the channel logits/llr values.
- Output:
[…,k], tf.float32 – Tensor containing bit-wise soft-estimates (or hard-decided bit-values) of all
kinformation bits.
Note
This decoder is fully differentiable and, thus, well-suited for gradient descent-based learning tasks such as learned code design [Ebada_Design].
As commonly done, we assume frozen bits are set to 0. Please note that - although its practical relevance is only little - setting frozen bits to 1 may result in affine codes instead of linear code as the all-zero codeword is not necessarily part of the code any more.
- property frozen_pos
Frozen positions for Polar decoding
- property hard_out
Indicates if decoder hard-decides outputs
- property info_pos
Information bit positions for Polar encoding
- property k
Number of information bits
- property llr_max
Maximum LLR value for internal calculations
- property n
Codeword length
- property num_iter
Number of decoding iterations
Utility Functions
- sionna.phy.fec.polar.utils.generate_5g_ranking(k, n, sort=True)[source]
Returns information and frozen bit positions of the 5G Polar code as defined in Tab. 5.3.1.2-1 in [3GPPTS38212] for given values of
kandn.- Input:
k (int) – The number of information bit per codeword.
n (int) – The desired codeword length. Must be a power of two.
sort (bool, (default True)) – Indicates if the returned indices are sorted.
- Output:
[frozen_pos, info_pos] – List:
frozen_pos (ndarray) – An array of ints of shape [n-k] containing the frozen position indices.
info_pos (ndarray) – An array of ints of shape [k] containing the information position indices.
- Raises:
AssertionError – If
kornare not positive ints.AssertionError – If
sortis not bool.AssertionError – If
kornare larger than 1024AssertionError – If
nis less than 32.AssertionError – If the resulting coderate is invalid (>1.0).
AssertionError – If
nis not a power of 2.
- sionna.phy.fec.polar.utils.generate_polar_transform_mat(n_lift)[source]
Generate the polar transformation matrix (Kronecker product).
- Input:
n_lift (int) – Defining the Kronecker power, i.e., how often is the kernel lifted.
- Output:
ndarray – Array of 0s and 1s of shape [2^n_lift , 2^n_lift] containing the Polar transformation matrix.
- sionna.phy.fec.polar.utils.generate_rm_code(r, m)[source]
Generate frozen positions of the (r, m) Reed Muller (RM) code.
- Input:
r (int) – The order of the RM code.
m (int) – log2 of the desired codeword length.
- Output:
frozen_pos (ndarray) – An array of ints of shape [n-k] containing the frozen position indices.
info_pos (ndarray) – An array of ints of shape [k] containing the information position indices.
n (int) – Resulting codeword length
k (int) – Number of information bits
d_min (int) – Minimum distance of the code.
- sionna.phy.fec.polar.utils.generate_dense_polar(frozen_pos, n, verbose=True)[source]
Generate naive (dense) Polar parity-check and generator matrix.
This function follows Lemma 1 in [Goala_LP] and returns a parity-check matrix for Polar codes.
Note
The resulting matrix can be used for decoding with the
LDPCBPDecoderclass. However, the resulting parity-check matrix is (usually) not sparse and, thus, not suitable for belief propagation decoding as the graph has many short cycles. Please considerPolarBPDecoderfor iterative decoding over the encoding graph.- Input:
frozen_pos (ndarray) – Array of int defining the
n-kindices of the frozen positions.n (int) – The codeword length.
verbose (bool, (default True)) – If True, the code properties are printed.
- Output:
pcm (ndarray of zeros and ones of shape [n-k, n]) – The parity-check matrix.
gm (ndarray of zeros and ones of shape [k, n]) – The generator matrix.
- References:
- [3GPPTS38212] (1,2,3,4,5,6,7,8,9,10,11,12,13)
ETSI 3GPP TS 38.212 “5G NR Multiplexing and channel coding”, v.16.5.0, 2021-03.
[Bioglio_Design] (1,2,3,4)V. Bioglio, C. Condo, I. Land, “Design of Polar Codes in 5G New Radio,” IEEE Communications Surveys & Tutorials, 2020. Online availabe https://arxiv.org/pdf/1804.04389.pdf
[Hui_ChannelCoding]D. Hui, S. Sandberg, Y. Blankenship, M. Andersson, L. Grosjean “Channel coding in 5G new radio: A Tutorial Overview and Performance Comparison with 4G LTE,” IEEE Vehicular Technology Magazine, 2018.
[Arikan_Polar] (1,2,3)E. Arikan, “Channel polarization: A method for constructing capacity-achieving codes for symmetric binary-input memoryless channels,” IEEE Trans. on Information Theory, 2009.
[Gross_Fast_SCL] (1,2)Seyyed Ali Hashemi, Carlo Condo, and Warren J. Gross, “Fast and Flexible Successive-cancellation List Decoders for Polar Codes.” IEEE Trans. on Signal Processing, 2017.
[Tal_SCL] (1,2)Ido Tal and Alexander Vardy, “List Decoding of Polar Codes.” IEEE Trans Inf Theory, 2015.
[Stimming_LLR]Alexios Balatsoukas-Stimming, Mani Bastani Parizi, Andreas Burg, “LLR-Based Successive Cancellation List Decoding of Polar Codes.” IEEE Trans Signal Processing, 2015.
[Hashemi_SSCL] (1,2)Seyyed Ali Hashemi, Carlo Condo, and Warren J. Gross, “Simplified Successive-Cancellation List Decoding of Polar Codes.” IEEE ISIT, 2016.
[Cammerer_Hybrid_SCL]Sebastian Cammerer, Benedikt Leible, Matthias Stahl, Jakob Hoydis, and Stephan ten Brink, “Combining Belief Propagation and Successive Cancellation List Decoding of Polar Codes on a GPU Platform,” IEEE ICASSP, 2017.
[Arikan_BP]E. Arikan, “A Performance Comparison of Polar Codes and Reed-Muller Codes,” IEEE Commun. Lett., vol. 12, no. 6, pp. 447-449, Jun. 2008.
[Forney_Graphs]G. D. Forney, “Codes on graphs: normal realizations,” IEEE Trans. Inform. Theory, vol. 47, no. 2, pp. 520-548, Feb. 2001.
[Ebada_Design]M. Ebada, S. Cammerer, A. Elkelesh and S. ten Brink, “Deep Learning-based Polar Code Design”, Annual Allerton Conference on Communication, Control, and Computing, 2019.
[Goala_LP]N. Goela, S. Korada, M. Gastpar, “On LP decoding of Polar Codes,” IEEE ITW 2010.