Multicell Topology

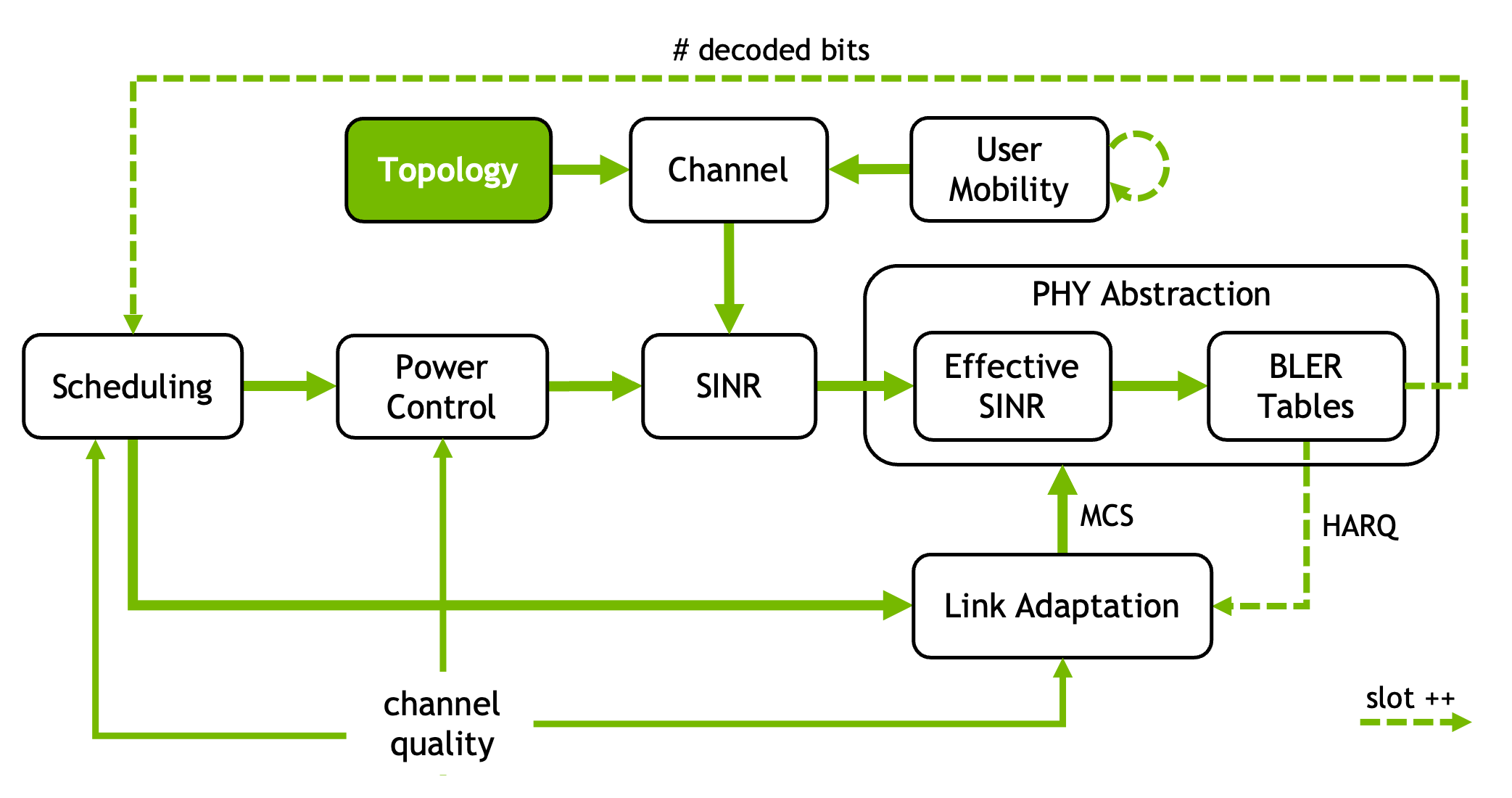
In system-level simulations with 3GPP channel modeling, it is customary to place cells on a spiral hexagonal grid. The grid is defined by the inter-site distance, determining the distance between any two adjacent hexagonal cell centers, and the number of rings of the grid, typically 1 or 2 (corresponding to 7 and 19 cells, hence 21 and 57 base stations, respectively).

To eliminate edge effects that would result in users at the cell borders experiencing reduced interference levels, the grid is usually wrapped around to create a seamless topology.

To learn how to place base stations and drop users on a hexagonal grid in Sionna, refer to the Hexagonal Grid Topology notebook.

class sionna.sys.topology.Hexagon(radius, coord, coord_type='offset', precision=None)

Class defining a hexagon placed in a hexagonal grid

Input:

• radius (float) – Hexagon radius, defined as the distance between the hexagon center and any of its corners

• coord ([2], list | tuple) – Coordinates of the hexagon center within the grid. If coord_type is euclid, the unit of measurement is meters [m].

• coord_type (‘offset’ (default) | ‘axial’ | ‘euclid’) – Coordinate type of coord

property coord_axial

Axial coordinates of the hexagon within a grid

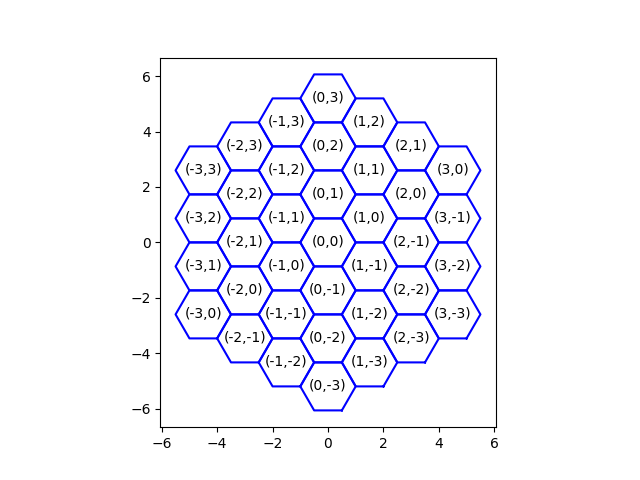
The basis of axial coordinates are 2D vectors ${\mathbf{b}}^{(1)}=(\frac{3}{2}r,\frac{\sqrt{3}}{2}r)$, ${\mathbf{b}}^{(2)}=(0,\sqrt{3}r)$. Thus, the relationship between axial coordinates $\mathbf{a}=(a_1,a_2)$ and their corresponding Euclidean ones $\mathbf{x}=(x_1,x_2)$ is the following:

$$\mathbf{x}=a_1{\mathbf{b}}^{(1)}+a_2{\mathbf{b}}^{(2)}$$

Type:

[2], tf.int32

coord_dict()

Returns the hexagon coordinates in the form of dictionary

Output:

dict – Dictionary containing the three hexagon coordinates, with key ‘euclid’, ‘offset’, ‘axial’

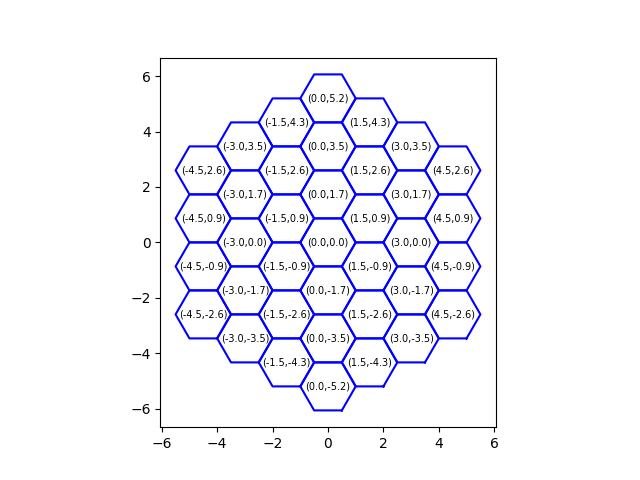
property coord_euclid

Euclidean coordinates of the hexagon within a grid

Type:

[2], tf.float

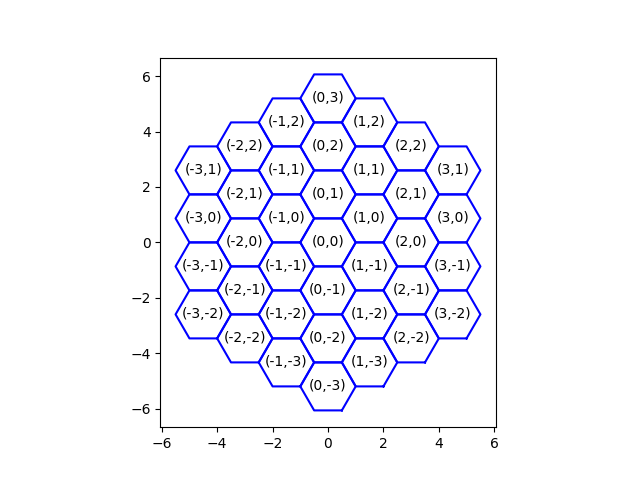
property coord_offset

Offset coordinates of the hexagon within a grid. The first (second, respectively) coordinate defines the horizontal (vertical, resp.) offset with respect to the grid center.

Type:

[2], tf.int32

corners()

Computes the Euclidean coordinates of the 6 corners of the hexagon

Output:

[6, 2], float – Euclidean coordinates of the 6 corners of the hexagon

neighbor(axial_direction_idx)

Returns the neighboring hexagon over the specified axial direction

Input:

axial_direction_idx (int) – Index determining the neighbor relative axial direction with respect to the current hexagon. Must be one of {0,…,5}.

Output:

Hexagon – Neighboring hexagon, in the axial relative direction

property radius

Hexagon radius, defined as the distance between its center and any of its corners

Type:

tf.float

class sionna.sys.topology.HexGrid(num_rings, cell_radius=None, cell_height=0.0, isd=None, center_loc=(0, 0), center_loc_type='offset', precision=None)

Creates a hexagonal spiral grid of cells, drops users uniformly at random in it uniformly at random and computes wraparound distances and base station positions

Cell sectors are numbered as follows:

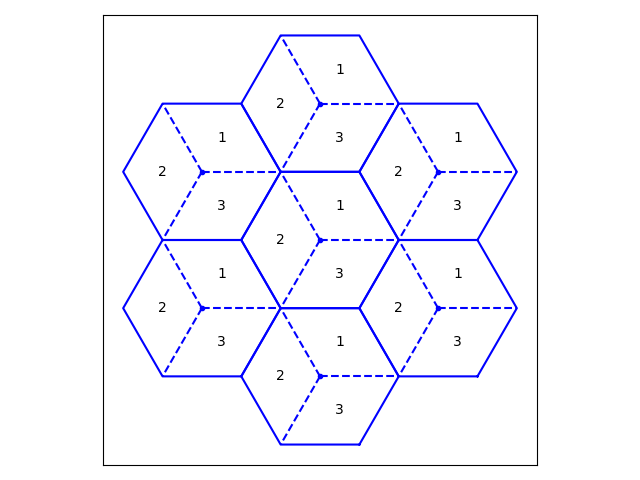
To eliminate border effects that would cause users at the edge of the grid to experience reduced interference, the wraparound principle artificially translates each base station to its closest corresponding “mirror” image in a neighboring hexagon for each user.

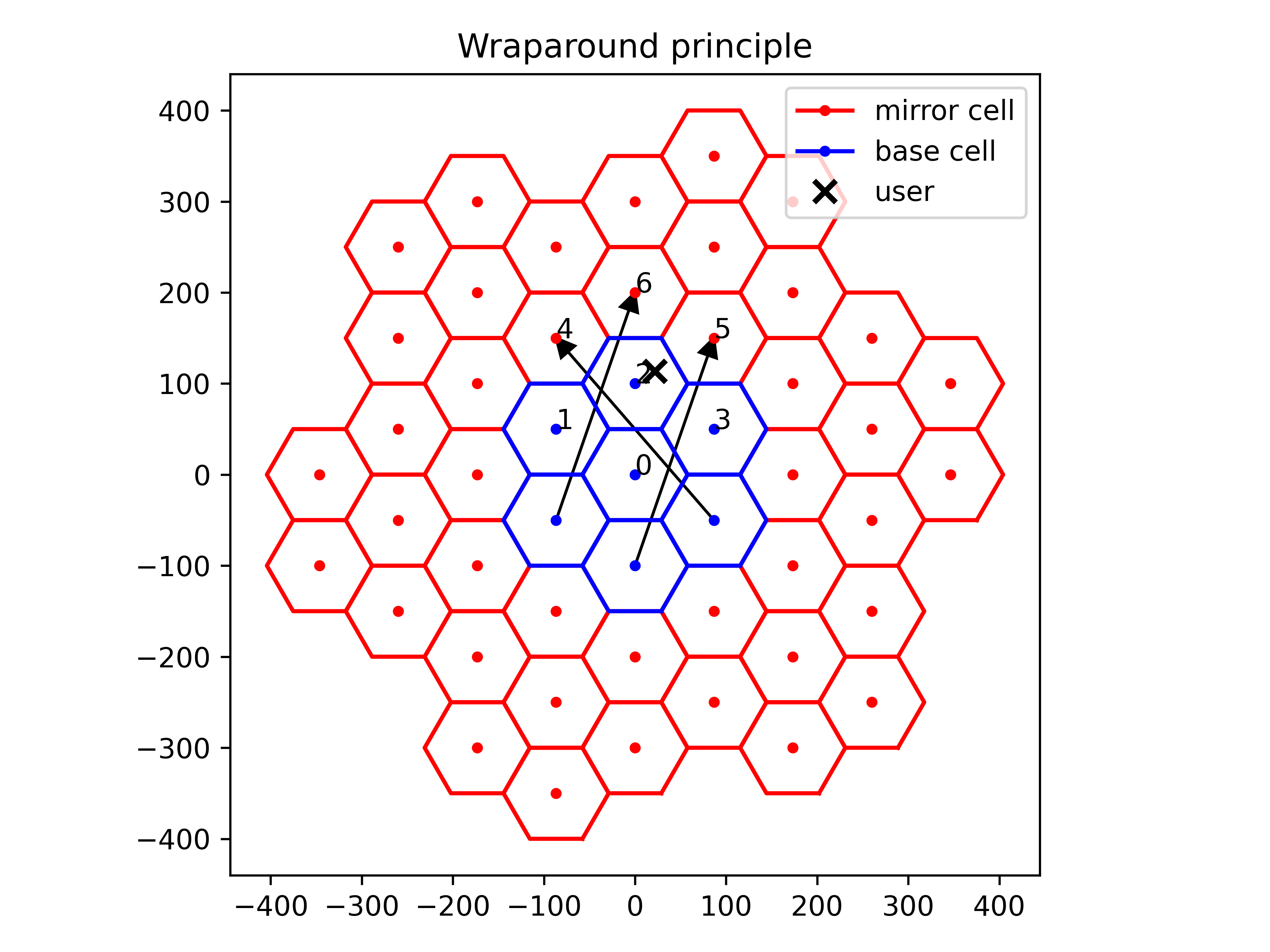
Parameters:

• num_rings (int) – Number of spiral rings in the grid

• cell_radius (float | None (default)) – Radius of each hexagonal cell in the grid, defined as the distance between the cell center and any of its corners. Either isd or cell_radius must be specified.

• cell_height (float (default: 0.)) – Cell height [m]

• isd (float | None (default)) – Inter-site distance. Either isd or cell_radius must be specified.

• center_loc ([2], list | tuple (default: (0,0))) – Coordinates of the grid center

• center_loc_type ('offset' (default) | 'axial' | 'euclid') – Coordinate type of center_coord

• precision (None (default) | “single” | “double”) – Precision used for internal calculations and outputs. If set to None, precision is used.

Input:

• batch_size (int) – Batch size

• num_ut_per_sector (int) – Number of users to sample per sector and per batch

• min_bs_ut_dist (float) – Minimum distance between a base station (BS) and a user [m]

• max_bs_ut_dist (float (default: None)) – Maximum distance between a base station (BS) and a user [m]. If None, it is not considered.

• ut_height (float (default: 0)) – User height, i.e., distance between the user and the X-Y plane [m]

Output:

• ut_loc ([batch_size, num_cells, num_sectors=3, num_ut_per_sector, 3], tf.float) – Location of users, dropped uniformly at random within each sector

• mirror_cell_per_ut_loc ([batch_size, num_cells, num_sectors=3, num_ut_per_sector, num_cells, 3], tf.float) – Coordinates of the artificial mirror cell centers, located at Euclidean distance wraparound_dist from each user

• wraparound_dist ([batch_size, num_cells, num_sectors=3, num_ut_per_sector, num_cells], tf.float) – Wraparound distance in the X-Y plane between each user and the cell centers

Example

from sionna.sys import HexGrid

# Create a hexagonal grid with a specified radius and number of rings
grid = HexGrid(cell_radius=1,
               cell_height=10,
               num_rings=1,
               center_loc=(0,0))

# Cell center locations
print(grid.cell_loc.numpy())
# [[ 0.         0.        10.       ]
#  [-1.5        0.8660254 10.       ]
#  [ 0.         1.7320508 10.       ]
#  [ 1.5        0.8660254 10.       ]
#  [ 1.5       -0.8660254 10.       ]
#  [ 0.        -1.7320508 10.       ]
#  [-1.5       -0.8660254 10.       ]]

property cell_height

Cell height [m]

Type:

float

property cell_loc

Euclidean coordinates of the cell centers [m]

Type:

[num_cells, 3], float

property cell_radius

Radius of any hexagonal cell in the grid [m]

Type:

float

property center_loc

Grid center coordinates in the X-Y plane, of type center_loc_type

Type:

[2], int | float

property grid

Collection of Hexagon objects corresponding to the cells in the grid

Type:

dict

property isd

Inter-site Euclidean distance [m]

Type:

float

property mirror_cell_loc

Euclidean (x,y,z) coordinates (axis=2) of the 6 mirror + base cells (axis=1) for each base cell (axis=0)

Type:

[num_cells, num_mirror_grids+1=7, 3], tf.float

property num_cells

Number of cells in the grid

Type:

int

property num_rings

Number of rings of the spiral grid

Type:

int

show(show_mirrors=False, show_coord=False, show_coord_type='euclid', show_sectors=False, coord_fontsize=8, fig=None, color='b', label='base')

Visualizes the base hexagonal grid and, if specified, the mirror grids too

Note that a mirror grid is a replica of the base grid, repeated around its boundaries to enable wraparound.

Input:

• show_mirrors (bool) – If True, then the mirror grids are visualized

• show_coord (bool) – If True, then the hexagon coordinates are visualized

• show_coord_type (str) – Type of coordinates to be visualized. Must be one of {‘offset’, ‘axial’, ‘euclid’}. Only effective if show_coord is True

• show_sectors (bool) – If True, then the three sectors within each hexagon are visualized

• coord_fontsize (int) – Coordinate fontsize. Only effective if show_coord is True

• fig (matplotlib.figure.Figure | None (default)) – Existing figure handle on which the grid is overlayed. If None, then a new figure is created

• color (str (default: ‘b’)) – Matplotlib line color

Output:

fig (matplotlib.figure.Figure) – Figure handle

sionna.sys.topology.gen_hexgrid_topology(batch_size, num_rings, num_ut_per_sector, scenario, min_bs_ut_dist=None, max_bs_ut_dist=None, isd=None, bs_height=None, min_ut_height=None, max_ut_height=None, indoor_probability=None, min_ut_velocity=None, max_ut_velocity=None, downtilt_to_sector_center=True, los=None, return_grid=False, precision=None)

Generates a batch of topologies with hexagonal cells placed on a spiral grid, 3 base stations per cell, and user terminals (UT) dropped uniformly at random across the cells

UT orientation and velocity are drawn uniformly randomly within the specified bounds, whereas the BSs point toward the center of their respective sector.

Parameters provided as None are set to valid values according to the chosen scenario (see [TR38901]).

The returned batch of topologies can be fed into the set_topology() method of the system level models, i.e. UMi, UMa, and RMa.

Input:

• batch_size (int) – Batch size

• num_ut (int) – Number of UTs to sample per batch example

• scenario (“uma” | “umi” | “rma” | “uma-calibration” | “umi-calibration”) – System level model scenario

• min_bs_ut_dist (None (default) | tf.float) – Minimum BS-UT distance [m]

• max_bs_ut_dist (None (default) | tf.float) – Maximum BS-UT distance [m]

• isd (None (default) | tf.float) – Inter-site distance [m]

• bs_height (None (default) | tf.float) – BS elevation [m]

• min_ut_height (None (default) | tf.float) – Minimum UT elevation [m]

• max_ut_height (None (default) | tf.float) – Maximum UT elevation [m]

• indoor_probability (None (default) | tf.float) – Probability of a UT to be indoor

• min_ut_velocity (None (default) | tf.float) – Minimum UT velocity [m/s]

• max_ut_velocity (None (default) | tf.float) – Maximim UT velocity [m/s]

• downtilt_to_sector_center (bool (default: True)) – If True, the BS is mechanically downtilted and points towards the sector center. Else, no mechanical downtilting is applied.

• los (bool | None (default)) – LoS/NLoS states of UTs

• return_grid (bool (default: False)) – Determines whether the HexGrid object is returned

• precision (None (default) | “single” | “double”) – Precision used for internal calculations and outputs. If set to None, precision is used.

Output:

• ut_loc ([batch_size, num_ut, 3], tf.float) – UT locations

• bs_loc ([batch_size, num_cells*3, 3], tf.float) – BS location

• ut_orientations ([batch_size, num_ut, 3], tf.float) – UT orientations [radian]

• bs_orientations ([batch_size, num_cells*3, 3], tf.float) – BS orientations [radian]. Oriented toward the center of the sector.

• ut_velocities ([batch_size, num_ut, 3], tf.float) – UT velocities [m/s]

• in_state ([batch_size, num_ut], tf.float) – Indoor/outdoor state of UTs. True means indoor, False means outdoor.

• los (None) – LoS/NLoS states of UTs. This is convenient for directly using the function’s output as input to set_topology(), ensuring that the LoS/NLoS states adhere to the 3GPP specification (Section 7.4.2 of TR 38.901).

• bs_virtual_loc ([batch_size, num_cells*3, num_ut, 3], tf.float) – Virtual, i.e., mirror, BS positions for each UT, computed according to the wraparound principle

• grid (HexGrid) – Hexagonal grid object. Only returned if return_grid is True.

Example

from sionna.phy.channel.tr38901 import PanelArray, UMi
from sionna.sys import gen_hexgrid_topology

# Create antenna arrays
bs_array = PanelArray(num_rows_per_panel = 4,
                      num_cols_per_panel = 4,
                      polarization = 'dual',
                      polarization_type = 'VH',
                      antenna_pattern = '38.901',
                      carrier_frequency = 3.5e9)

ut_array = PanelArray(num_rows_per_panel = 1,
                      num_cols_per_panel = 1,
                      polarization = 'single',
                      polarization_type = 'V',
                      antenna_pattern = 'omni',
                      carrier_frequency = 3.5e9)
# Create channel model
channel_model = UMi(carrier_frequency = 3.5e9,
                    o2i_model = 'low',
                    ut_array = ut_array,
                    bs_array = bs_array,
                    direction = 'uplink')
# Generate the topology
topology = gen_hexgrid_topology(batch_size=100,
                                num_rings=1,
                                num_ut_per_sector=3,
                                scenario='umi')
# Set the topology
channel_model.set_topology(*topology)
channel_model.show_topology()

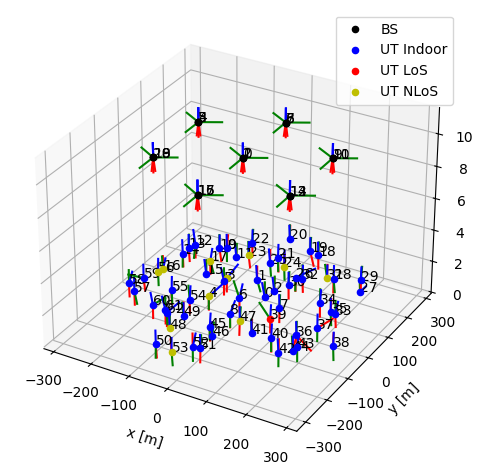
sionna.sys.topology.get_num_hex_in_grid(num_rings)

Computes the number of hexagons in a spiral hexagonal grid with a given number of rings $N$. It equals $1+3N(N+1)$

Input:

num_rings (int) – Number of rings of the hexagonal spiral grid

Output:

int – Number of hexagons in the spiral hexagonal grid

sionna.sys.topology.convert_hex_coord(coord, conversion_type, hex_radius=None, precision=None)

Converts the center coordinates of a hexagon within a grid between any two of the types {“offset”, “axial”, “euclid”}

Input:

• coord ([…, 2], tf.int | tf.float) – Coordinates of the center of a hexagon contained in a hexagonal grid

• conversion_type (‘offset2euclid’ | ‘euclid2offset’ | ‘euclid2axial’ | ‘offset2axial’ | ‘axial2offset’ | ‘axial2euclid’) – Type of coordinate conversion

• hex_radius ([…], tf.float | None (default)) – Hexagon radius, i.e., distance between its center and any of its corners. It must be specified if convert_type is ‘offset2euclid’.

• precision (None (default) | “single” | “double”) – Precision used for internal calculations and outputs. If set to None, precision is used.

Output:

[2], tf.float | tf.int – Output coordinates

References:

[HexGrid]

Amit Patel’s blog, Hexagonal Grids