Power Control

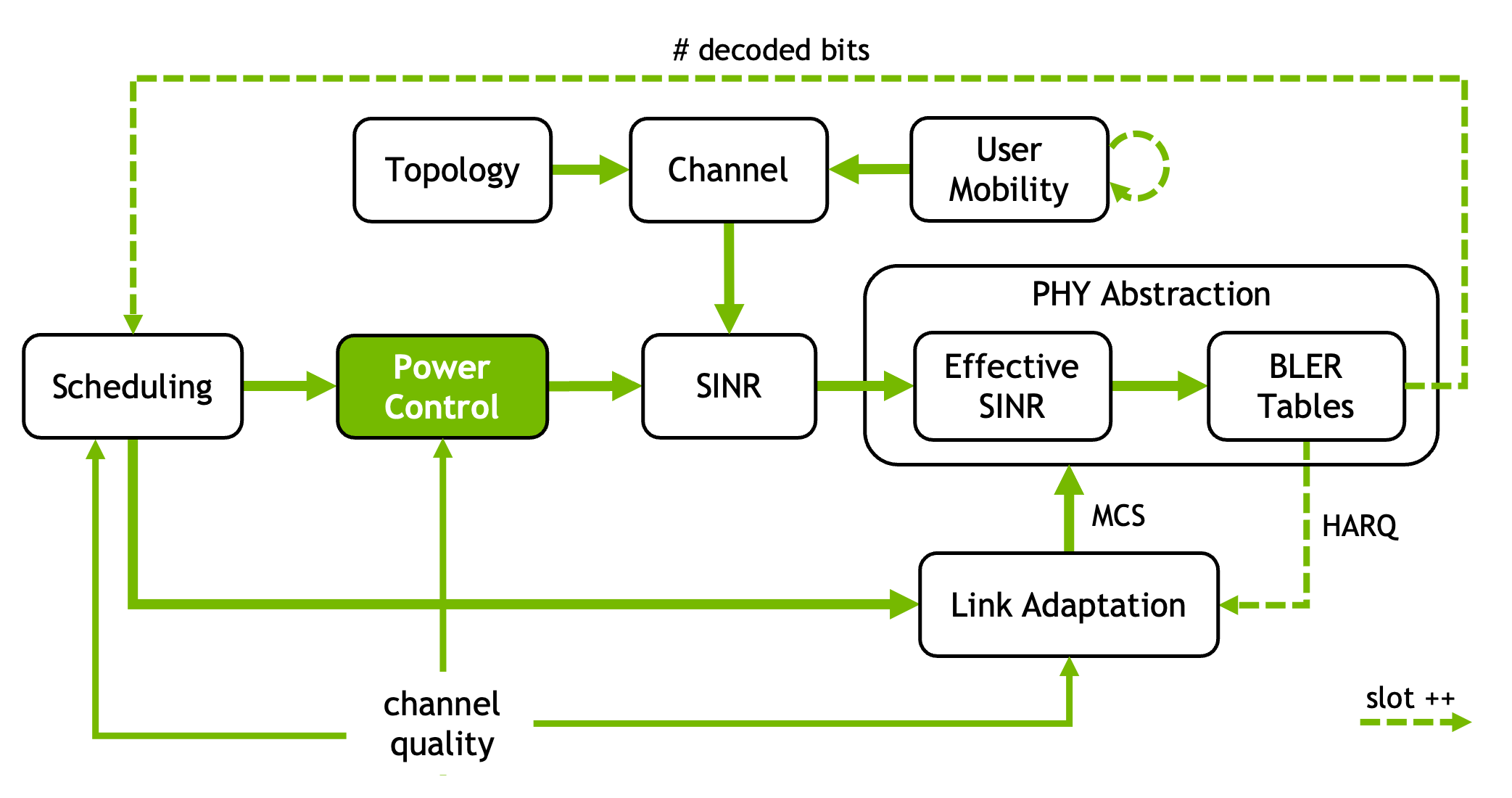
Upon scheduling users to available resources, the transmission power must be adjusted to ensure that users receive the desired quality of service while minimizing interference to other users.

In the uplink, the user terminal typically aims at (partially) compensating for the pathloss to reach a target received power at the base station. In the downlink, the base station distributes the available power budget across users according to a certain fairness criterion.

For an example of how to adjust transmission power in Sionna, refer to the Power Control notebook.

Uplink

sionna.sys.open_loop_uplink_power_control(pathloss, num_allocated_subcarriers, alpha=1.0, p0_dbm=-90.0, ut_max_power_dbm=26.0, precision=None)[source]

Implements an open-loop uplink power control procedure inspired by 3GPP TS 38.213, Section 7.1.1 [3GPP38213].

For each user, the uplink transmission power $P^{UL}$ is computed as:

P^{UL} = min {P_{0} + α P L + 10 \log_{10} (# PRB), P^{\max}} [dBm]

where $P^{\max}$ is the maximum power, $P_{0}$ [dBm] is the target received power per Physical Resource Block (PRB), $P L$ is the pathloss and $α \in [0, 1]$ is the pathloss compensation factor.

Note that if $α = 1$ , the pathloss is fully compensated and the power per PRB received by the base station equals $P_{0}$ [dBm], assuming $P^{\max}$ is not reached. Lower values of $α$ can help reducing interference caused to neighboring cells.

With respect to 3GPP TS 38.213, additional factors such as closed-loop control and transport format adjustments are here ignored

Input:

pathloss ([…, num_ut], tf.float) – Pathloss for each user relative to the serving base station, in linear scale
num_allocated_subcarriers ([…, num_ut]) – Number of allocated subcarriers for each user
alpha ([…, num_ut], tf.float | float (default: 1.0)) – Pathloss compensation factor. If a float, the same value is applied to all users.
p0_dbm ([…, num_ut], tf.float | float (default: -90.0)) – Target received power per PRB. If a float, the same value is applied to all users.
ut_max_power_dbm ([…, num_ut], tf.float | float (default: 26.0)) – Maximum transmit power [dBm] for each user. If a float, the same value is applied to all users.
precision (None (default) | “single” | “double”) – Precision used for internal calculations and outputs. If set to None, precision is used.

Output:

tx_power_per_ut ([…, num_ut], tf.float) – Uplink transmit power [W] for each user, across subcarriers, streams and time steps

Example

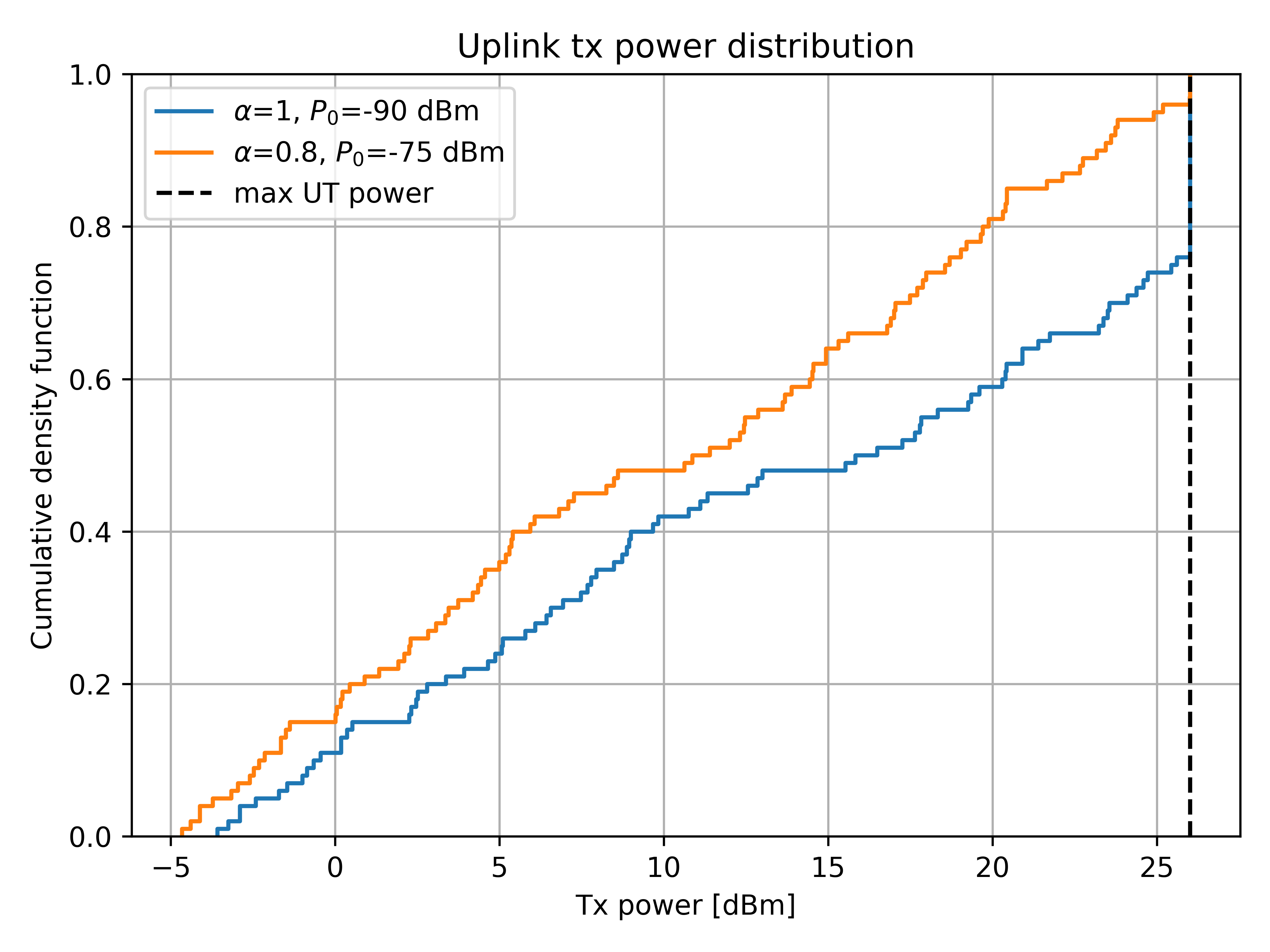
import matplotlib.pyplot as plt
from sionna.sys import open_loop_uplink_power_control
from sionna.phy import config
from sionna.phy.utils import db_to_lin, watt_to_dbm

# N. users
num_ut = 100
# Max tx power per UT
ut_max_power_dbm = 26  # [dBm]
# Pathloss [dB]
pathloss_db = config.tf_rng.uniform([num_ut], minval=80, maxval=120)
# N. allocated subcarriers per UT
num_allocated_subcarriers = tf.fill([num_ut], 40)
# Parameters (pathloss compensation factor, reference rx power)
alpha_p0 = [(1, -90), (.8, -75)]

for alpha, p0, in alpha_p0:
    # Power allocation
    tx_power_per_ut = open_loop_uplink_power_control(db_to_lin(pathloss_db),
                                num_allocated_subcarriers=num_allocated_subcarriers,
                                alpha=alpha,
                                p0_dbm=p0,
                                ut_max_power_dbm=ut_max_power_dbm)
    # Plot CDF of tx power
    plt.ecdf(watt_to_dbm(tx_power_per_ut), label=fr'$\alpha$={alpha}, $P_0$={p0} dBm')
# Plot max UT power
plt.plot([ut_max_power_dbm]*2, [0, 1], 'k--', label='max UT power')

plt.legend()
plt.grid()
plt.xlabel('Tx power [dBm]')
plt.ylabel('Cumulative density function')
plt.title('Uplink tx power distribution')
plt.show()

Downlink

sionna.sys.downlink_fair_power_control(pathloss, interference_plus_noise, num_allocated_re, bs_max_power_dbm=56.0, guaranteed_power_ratio=0.5, fairness=0.0, return_lagrangian=False, precision=None, **kwargs)[source]

Allocates the downlink transmit power fairly across all users served by a single base station (BS)

The maximum BS transmit power $\overset{―}{P}$ is distributed across users by solving the following optimization problem:

\begin{array}{r} \begin{aligned} p^{*} = {argmax}_{p} & \sum_{u = 1}^{U} g^{(f)} (r_{u} \log (1 + p_{u} q_{u})) \\ s . t . & \sum_{u = 1}^{U} r_{u} p_{u} = \overset{―}{P} \\ r_{u} p_{u} \geq ρ \frac{\overset{―}{P}}{U}, \forall u = 1, \dots, U \end{aligned} \end{array}

where $q_{u}$ represents the estimated channel quality, defined as the ratio between the channel gain (being the inverse of pathloss) and the interference plus noise ratio, $r_{u} > 0$ denotes the number of allocated resources, and $p_{u}$ is the per-resource allocated power, for every user $u$ .

The parameter $ρ \in [0; 1]$ denotes the guaranteed power ratio; if set to 1, the power is distributed uniformly across all users.

The fairness function $g^{(f)}$ is defined as in [MoWalrand]:

\begin{array}{r} \begin{matrix} g^{(f)} (x) = {\begin{cases} \log (x), f = 1 \\ \frac{x^{1 - f}}{1 - f}, \forall f > 0, f \neq 1. \end{cases} \end{matrix} \end{array}

When the fairness parameter $f = 0$ , the sum of utilities $\log (1 + p_{u} q_{u})$ is maximized, leading to a waterfilling-like solution (see, e.g., [Tse]). As $f$ increases, the allocation becomes increasingly egalitarian. The case $f = 1$ maximizes proportional fairness; as $f \to \infty$ , the solution approaches a max-min allocation.

For optimal power allocations $p_{u}^{*} > \frac{\overset{―}{P}}{U r_{u}}$ , the Karush-Kuhn-Tucker (KKT) conditions can be expressed as:

[r_{u} \log (1 + p_{u}^{*} q_{u})]^{f} (1 + p_{u}^{*} q_{u}) = q_{u} μ^{- 1}, \forall u

where $μ$ is the Lagrangian multiplier associated with the constraint on the total transmit power.

This function returns the optimal power allocation $r_{u} p_{u}^{*}$ and the corresponding utility $r_{u} \log (1 + p_{u}^{*} q_{u})$ , for each user $u = 1, \dots, U$ . If return_lagrangian is True, $μ^{- 1}$ is returned, too.

Input:

pathloss ([…, num_ut], tf.float) – Pathloss for each user in linear scale
interference_plus_noise ([…, num_ut], tf.float | float) – Interference plus noise [Watt] for each user. If float, the same value is assigned to all users.
num_allocated_re ([…, num_ut], tf.int32 | int) – Number of allocated resources to each user. If int, the same value is assigned to all users.
bs_max_power_dbm ([…], tf.float | float (default: 56.)) – Maximum transmit power for the base station [dBm]. If float, the same value is assigned to all batches.
guaranteed_power_ratio (float (default: 0.2)) – The power allocated to a user is guaranteed to exceed a portion guaranteed_power_ratio of bs_max_power_dbm divided by the number of scheduled users. Must be within [0;1].
fairness (float (default: 0.)) – Fairness parameter. If 0, the sum of utilities is maximized; when 1, proportional fairness is achieved. As fairness increases, the optimal allocation approaches a max-min one.
return_lagrangian (bool (default: False)) – If True, the inverse of the optimal Lagrangian multiplier mu_inv_star is returned
precision (None (default) | “single” | “double”) – Precision used for internal calculations and outputs. If set to None, precision is used.
kwargs (dict) – Additional inputs for bisection_method() used to compute the optimal power allocation, such as eps_x, eps_y, max_n_iter, step_expand

Output:

tx_power ([…, num_ut], tf.float) – Optimal downlink power allocation $p_{u}^{*}$ [Watt] for each user $u$
utility ([…, num_ut], tf.float) – Optimal utility for each user, computed as $r_{u} \log (1 + p_{u}^{*} q_{u})$ for user $u$
mu_inv_star ([…], tf.float) – Inverse of the optimal Lagrangian multiplier $μ$ associated with the total power constraint. Only returned if return_lagrangian is True.

Example

import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
from sionna.phy import config
from sionna.phy.utils import db_to_lin, dbm_to_watt
from sionna.sys import downlink_fair_power_control
config.seed = 45

# Evaluate the impact of 'fairness' and 'guaranteed_power_ratio'
# parameters on the DL power allocation and utility

# Guaranteed power ratios
guaranteed_power_ratio_vec = [0, .35, .7]

# Fairness parameters
fairness_vec = [0, 1, 2, 5]

# N. users
num_ut = 30

# BS tx power
bs_max_power_dbm = 56
max_power_bs = dbm_to_watt(bs_max_power_dbm)

# Interference plus noise
interference_plus_noise = 5e-10  # [W]

# Generate random pathloss
pathloss_db = config.tf_rng.uniform(
    [num_ut], minval=70, maxval=110)  # [dB]
pathloss = db_to_lin(pathloss_db)

# Channel quality
cq = 1 / (pathloss * interference_plus_noise)

fig, axs = plt.subplots(3, len(guaranteed_power_ratio_vec),
                        figsize=(3.5*len(guaranteed_power_ratio_vec), 8),
                        sharey='row')
fig.subplots_adjust(top=0.8)
for ax in axs.flatten():
    ax.yaxis.set_tick_params(labelbottom=True)
    ax.grid()
    ax.set_xlabel(r'User terminal $u$', fontsize=12)

# Show channel quality in decreasing order
ind_sort = np.argsort(cq)[::-1]
axs[0, 1].plot(10*np.log10(cq)[ind_sort], '.-')
axs[0, 1].set_ylabel(r'$q_u$ [dB]', fontsize=12)
axs[0, 1].set_title('Channel quality')

for ii, guar_ratio in enumerate(guaranteed_power_ratio_vec):
    # Guaranteed power for each user
    guaranteed_power = guar_ratio * max_power_bs / num_ut

    for fairness in fairness_vec:
        # DL fair power allocation
        tx_power, utility = downlink_fair_power_control(
            pathloss,
            interference_plus_noise=interference_plus_noise,
            num_allocated_re=1,
            bs_max_power_dbm=bs_max_power_dbm,
            guaranteed_power_ratio=guar_ratio,
            fairness=fairness)

        # Show utility
        axs[2, ii].plot(utility.numpy()[ind_sort], '.-',
                    label=f'fairness = {fairness}')
        # Show transmit power
        axs[1, ii].plot(tx_power.numpy()[ind_sort], '.-',
                    label=f'fairness = {fairness}')

    axs[1, ii].plot([0, num_ut-1], [guaranteed_power]*2, '--k', label='guaranteed power')
    axs[1, ii].set_ylabel(r'Power $r_u p^*_u$ [W]', fontsize=12)
    axs[1, ii].legend(fontsize=9)
    axs[2, ii].set_ylabel(r'Utility $r_u \log(1+p^*_u q_u)$', fontsize=12)
    axs[1, ii].set_title(f'Guaranteed power ratio = {guar_ratio}')

fig.suptitle('Downlink fair power control', y=.98, fontsize=18)
fig.tight_layout()
fig.delaxes(axs[0, 0])
fig.delaxes(axs[0, 2])
plt.show()

References:

[MoWalrand]

J. Mo and J. Walrand, “Fair end-to-end window-based congestion control,” IEEE/ACM Transactions on networking, vol. 8, no. 5, pp. 556–567, Oct. 2000.

[3GPP38213]

3GPP TS 38.213. “NR; Physical layer procedures for control”.