Utility Functions#

Complex-valued tensors#

sionna.rt.utils.cpx_abs(x: Tuple[drjit.llvm.ad.TensorXf, drjit.llvm.ad.TensorXf]) → drjit.llvm.ad.TensorXf[source]#

Element-wise absolute value of a complex-valued tensor

The tensor is represented as a tuple of two real-valued tensors, corresponding to the real and imaginary part, respectively.

Parameters:

x (Tuple[drjit.llvm.ad.TensorXf, drjit.llvm.ad.TensorXf]) – A tensor

sionna.rt.utils.cpx_abs_square(x: Tuple[drjit.llvm.ad.TensorXf, drjit.llvm.ad.TensorXf]) → drjit.llvm.ad.TensorXf[source]#

Element-wise absolute squared value of a complex-valued tensor

The tensor is represented as a tuple of two real-valued tensors, corresponding to the real and imaginary part, respectively.

Parameters:

x (Tuple[drjit.llvm.ad.TensorXf, drjit.llvm.ad.TensorXf]) – A tensor

sionna.rt.utils.cpx_add(a: Tuple[drjit.llvm.ad.TensorXf, drjit.llvm.ad.TensorXf], b: Tuple[drjit.llvm.ad.TensorXf, drjit.llvm.ad.TensorXf]) → Tuple[drjit.llvm.ad.TensorXf, drjit.llvm.ad.TensorXf][source]#

Element-wise addition of two complex-valued tensors

Each tensor is represented as a tuple of two real-valued tensors, corresponding to the real and imaginary part, respectively.

Parameters:
sionna.rt.utils.cpx_convert(x: Tuple[drjit.llvm.ad.TensorXf, drjit.llvm.ad.TensorXf], out_type: Literal['numpy', 'jax', 'tf', 'torch'])[source]#

Converts a complex-valued tensor to any of the supported frameworks

The tensor is represented as a tuple of two real-valued tensors, corresponding to the real and imaginary part, respectively.

Note that the chosen framework must be installed for this function to work.

Parameters:
sionna.rt.utils.cpx_div(a: Tuple[drjit.llvm.ad.TensorXf, drjit.llvm.ad.TensorXf], b: Tuple[drjit.llvm.ad.TensorXf, drjit.llvm.ad.TensorXf]) → Tuple[drjit.llvm.ad.TensorXf, drjit.llvm.ad.TensorXf][source]#

Element-wise division of a complex-valued tensor by another

Each tensor is represented as a tuple of two real-valued tensors, corresponding to the real and imaginary part, respectively.

Parameters:
sionna.rt.utils.cpx_exp(x: Tuple[drjit.llvm.ad.TensorXf, drjit.llvm.ad.TensorXf]) → Tuple[drjit.llvm.ad.TensorXf, drjit.llvm.ad.TensorXf][source]#

Element-wise exponential of a complex-valued tensor

The tensor is represented as a tuple of two real-valued tensors, corresponding to the real and imaginary part, respectively.

Parameters:

x (Tuple[drjit.llvm.ad.TensorXf, drjit.llvm.ad.TensorXf]) – A tensor

sionna.rt.utils.cpx_mul(a: Tuple[drjit.llvm.ad.TensorXf, drjit.llvm.ad.TensorXf], b: Tuple[drjit.llvm.ad.TensorXf, drjit.llvm.ad.TensorXf]) → Tuple[drjit.llvm.ad.TensorXf, drjit.llvm.ad.TensorXf][source]#

Element-wise multiplication of two complex-valued tensors

Each tensor is represented as a tuple of two real-valued tensors, corresponding to the real and imaginary part, respectively.

Parameters:
sionna.rt.utils.cpx_sqrt(x: Tuple[drjit.llvm.ad.TensorXf, drjit.llvm.ad.TensorXf]) → drjit.llvm.ad.TensorXf[source]#

Element-wise square root of a complex-valued tensor

The tensor is represented as a tuple of two real-valued tensors, corresponding to the real and imaginary part, respectively.

The following formula is implemented to compute the square roots of complex numbers: https://en.wikipedia.org/wiki/Square_root#Algebraic_formula

Parameters:

x (Tuple[drjit.llvm.ad.TensorXf, drjit.llvm.ad.TensorXf]) – A tensor

sionna.rt.utils.cpx_sub(a: Tuple[drjit.llvm.ad.TensorXf, drjit.llvm.ad.TensorXf], b: Tuple[drjit.llvm.ad.TensorXf, drjit.llvm.ad.TensorXf]) → Tuple[drjit.llvm.ad.TensorXf, drjit.llvm.ad.TensorXf][source]#

Element-wise substraction of a complex-valued tensor from another

Each tensor is represented as a tuple of two real-valued tensors, corresponding to the real and imaginary part, respectively.

Parameters:

Electromagnetics#

sionna.rt.utils.complex_relative_permittivity(eta_r: drjit.llvm.ad.Float, sigma: drjit.llvm.ad.Float, omega: drjit.llvm.ad.Float) → drjit.llvm.ad.Complex2f[source]#

Computes the complex relative permittivity of a material as defined in (9)

Parameters:
sionna.rt.utils.fresnel(x: drjit.llvm.ad.Float) → drjit.llvm.ad.Complex2f[source]#

Computes the complex-valued Fresnel integral

The complex-valued Fresnel integral is defined as:

(55)#\[F_c(x) = \int_0^{\sqrt{\frac{2x}{\pi}}} \exp\left(j\frac{\pi s^2}{2}\right)ds = C(x) + jS(x)\]

This function computes an approximation of this integral as described in Section 2.7 of [ITURP52615]. It has sufficient accuracy for most purposes. Note that we let the upper limit of the integral be \(\sqrt{2x/\pi}\) instead of \(x\), which is different from the definition in [ITURP52615]. Thus, evaluating \(F_c(x)\) corresponds to \(F_c(\sqrt{2x/\pi})\) in the classical definition.

Parameters:

x (drjit.llvm.ad.Float) – Argument of the Fresnel integral

Returns:

Complex-valued Fresnel integral

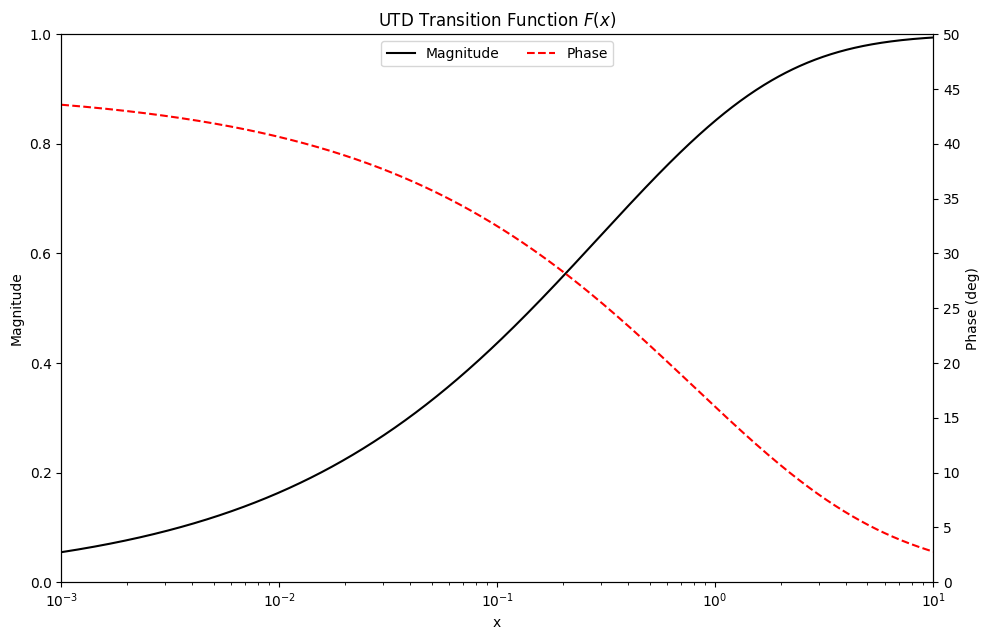
sionna.rt.utils.f_utd(x: drjit.llvm.ad.Float) → drjit.llvm.ad.Complex2f[source]#

Computes the UTD transition function

The UTD transition function is defined as:

\[F(x) = \sqrt{\frac{\pi x}{2}} e^{jx}\left(1+j-2jF_c^*(x) \right)\]

where \(F_c^*(x)\) is the complex conjugate of the Fresnel integral (55).

Parameters:

x (drjit.llvm.ad.Float) – Argument of the UTD transition function

Returns:

Real and imaginary parts of the UTD transition function

Example#

The following code snippet produces a visualization of the magnitude and phase of the UTD transition function which matches that of Fig. 6 in [Kouyoumjian74].

import numpy as np
import matplotlib.pyplot as plt
import drjit as dr
import mitsuba as mi
mi.set_variant("cuda_ad_mono_polarized", "llvm_ad_mono_polarized")
from sionna.rt.utils import f_utd, cpx_convert

x = np.logspace(-3, 1, 1000)
y = cpx_convert(f_utd(mi.Float(x)), "numpy")
fig, ax1 = plt.subplots(figsize=(10, 6.5))

# Plot magnitude with label
mag_line, = ax1.semilogx(x, np.abs(y), "k-", label="Magnitude")
ax1.set_ylabel("Magnitude")

# Create second y-axis
ax2 = plt.twinx()

# Plot phase with label
phase_line, = ax2.semilogx(x, np.angle(y, deg=True), "r--", label="Phase")
ax2.set_ylabel("Phase (deg)")

# Combine lines from both axes for the legend
lines = [mag_line, phase_line]
labels = [line.get_label() for line in lines]

# Add legend with both lines
ax1.legend(lines, labels, loc='upper center', frameon=True, ncol=2)

# Set title and x label
plt.title(r"UTD Transition Function $F(x)$")
ax1.set_xlabel("x")

# Adjust limits and ticks
ax1.set_xlim(x.min(), x.max())
ax1.set_ylim(np.abs(y).min(), np.abs(y).max())
ax2.set_ylim(np.angle(y, deg=True).min(), np.angle(y, deg=True).max())
ax1.set_yticks(np.linspace(0, 1, 6))
ax2.set_yticks(np.linspace(0, 50, 11))

plt.show()
../../_images/f_utd.png
sionna.rt.utils.fresnel_reflection_coefficients_simplified(cos_theta: drjit.llvm.ad.Float, eta: drjit.llvm.ad.Complex2f) → Tuple[drjit.llvm.ad.Complex2f, drjit.llvm.ad.Complex2f][source]#

Computes the Fresnel transverse electric and magnetic reflection coefficients assuming an incident wave propagating in vacuum (34)

Parameters:
Returns:

Transverse electric \(r_{\perp}\) and magnetic \(r_{\parallel}\) Fresnel reflection coefficients

sionna.rt.utils.itu_coefficients_single_layer_slab(cos_theta: drjit.llvm.ad.Float, eta: drjit.llvm.ad.Complex2f, d: drjit.llvm.ad.Float, wavelength: drjit.llvm.ad.Float) → Tuple[drjit.llvm.ad.Complex2f, drjit.llvm.ad.Complex2f, drjit.llvm.ad.Complex2f, drjit.llvm.ad.Complex2f][source]#

Computes the single-layer slab Fresnel transverse electric and magnetic reflection and refraction coefficients assuming the incident wave propagates in vacuum using recommendation ITU-R P.2040 [ITURP20403]

More precisely, this function implements equations (43) and (44) from [ITURP20403].

Parameters:
Returns:

Transverse electric reflection coefficient \(R_{eTE}\), transverse magnetic reflection coefficient \(R_{eTM}\), transverse electric refraction coefficient \(T_{eTE}\), and transverse magnetic refraction coefficient \(T_{eTM}\)

Geometry#

sionna.rt.utils.phi_hat(phi: drjit.llvm.ad.Float) → mitsuba.Vector3f[source]#

Computes the spherical unit vector \(\hat{\boldsymbol{\varphi}}(\theta, \varphi)\) as defined in (1)

Parameters:

phi (drjit.llvm.ad.Float) – Azimuth angle \(\varphi\) [rad]

sionna.rt.utils.theta_hat(theta: drjit.llvm.ad.Float, phi: drjit.llvm.ad.Float) → mitsuba.Vector3f[source]#

Computes the spherical unit vector \(\hat{\boldsymbol{\theta}}(\theta, \varphi)\) as defined in (1)

Parameters:
sionna.rt.utils.r_hat(theta: drjit.llvm.ad.Float, phi: drjit.llvm.ad.Float) → mitsuba.Vector3f[source]#

Computes the spherical unit vetor \(\hat{\mathbf{r}}(\theta, \phi)\) as defined in (1)

Parameters:
sionna.rt.utils.theta_phi_from_unit_vec(v: mitsuba.Vector3f) → Tuple[drjit.llvm.ad.Float, drjit.llvm.ad.Float][source]#

Computes zenith and azimuth angles (\(\theta,\varphi\)) from unit-norm vectors as described in (2)

Parameters:

v (mitsuba.Vector3f) – Unit vector

Returns:

Zenith angle \(\theta\) [rad] and azimuth angle \(\varphi\) [rad]

sionna.rt.utils.rotation_matrix(angles: mitsuba.Point3f) → drjit.llvm.ad.Matrix3f[source]#

Computes the rotation matrix as defined in (3)

The closed-form expression in (7.1-4) [TR38901_RT] is used.

Parameters:

angles (mitsuba.Point3f) – Angles for the rotations \((\alpha,\beta,\gamma)\) [rad] that define rotations about the axes \((z, y, x)\), respectively

Jones calculus#

sionna.rt.utils.implicit_basis_vector(k: mitsuba.Vector3f) → mitsuba.Vector3f[source]#

Returns a reference frame basis vector for a Jones vector, representing a transverse wave propagating in direction k

The spherical basis vector \(\hat{\boldsymbol{\theta}}(\theta, \varphi)\) (1) is used as basis vector, where the zenith and azimuth angles are obtained from the unit vector k.

Parameters:

k (mitsuba.Vector3f) – A unit vector corresponding to the direction of propagation of a transverse wave

Returns:

A basis vector orthogonal to k

sionna.rt.utils.jones_matrix_rotator(k: mitsuba.Vector3f, s_current: mitsuba.Vector3f, s_target: mitsuba.Vector3f) → drjit.llvm.ad.Matrix2f[source]#

Constructs the 2D change-of-basis matrix to rotate the reference frame of a Jones vector representing a transverse wave propagating in direction k from basis vector s_current to basis vector s_target

Parameters:
sionna.rt.utils.jones_matrix_rotator_flip_forward(k: mitsuba.Vector3f) → drjit.llvm.ad.Matrix2f[source]#

Constructs the 2D change-of-basis matrix that flips the direction of propagation of the reference frame of a Jones vector representing a transverse wave from the basis vector corresponding to k to the one corresponding to -k

This is useful to evaluate the antenna pattern of a receiver, as the pattern needs to be rotated to match the frame in which the incident wave is represented.

Note that the rotation matrix returned by this function is a diagonal matrix:

\[\begin{split}\mathbf{R} = \begin{bmatrix} \begin{array}{c c} c & 0 \\ 0 & -c \end{array} \end{bmatrix}\end{split}\]

where:

\[c = \mathbf{s_c}^\textsf{T} \mathbf{s_t}\]

and \(\mathbf{s_c}\) and \(\mathbf{s_t}\) are the basis vectors corresponding to k and -k, respectively, and computed using implicit_basis_vector().

Parameters:

k (mitsuba.Vector3f) – Current direction of propagation as a unit vector

sionna.rt.utils.to_world_jones_rotator(to_world: drjit.llvm.ad.Matrix3f, k_local: mitsuba.Vector3f) → drjit.llvm.ad.Matrix2f[source]#

Constructs the 2D change-of-basis matrix to rotate the reference frame of a Jones vector representing a transverse wave with k_local as direction of propagation from the local implicit frame to the world implicit frame

Parameters:
sionna.rt.utils.jones_matrix_to_world_implicit(c1: drjit.llvm.ad.Complex2f, c2: drjit.llvm.ad.Complex2f, to_world: drjit.llvm.ad.Matrix3f, k_in_local: mitsuba.Vector3f, k_out_local: mitsuba.Vector3f) → drjit.llvm.ad.Matrix4f[source]#

Builds the Jones matrix that models a specular reflection or a refraction

c1 and c2 are Fresnel coefficients that depend on the composition of the scatterer. k_in_local and k_out_local are the direction of propagation of the incident and scattered wave, respectively, represented in the local frame of the interaction. Note that in the local frame of the interaction, the z-axis vector corresponds to the normal to the scatterer surface at the interaction point.

The returned matrix operates on the incident wave represented in the implicit world frame. The resulting scattered wave is also represented in the implicit world frame. This is ensured by applying a left and right rotation matrix to the 2x2 diagonal matrix containing the Fresnel coefficients, which operates on the local frame having the transverse electric component as basis vector:

\[\mathbf{J} = \mathbf{R_O} \mathbf{D} \mathbf{R_I}^\textsf{T}\]

where:

\[\begin{split}\mathbf{D} = \begin{bmatrix} \begin{array}{c c} \texttt{c1} & 0 \\ 0 & \texttt{c2} \end{array} \end{bmatrix}\end{split}\]

and \(\mathbf{R_I}\) (\(\mathbf{R_O}\)) is the change-of-basis matrix from the local frame using the transverse electric direction as basis vector to the world implicit frame for the incident (scattered) wave.

This function returns the \(4 \times 4\) real-valued matrix equivalent to \(\mathbf{J}\):

\[\begin{split}\mathbf{M} = \begin{bmatrix} \begin{array}{c c} \Re\{\mathbf{J}\} & -\Im\{\mathbf{J}\} \\ \Im\{\mathbf{J}\} & \Re\{\mathbf{J}\} \end{array} \end{bmatrix}\end{split}\]

where \(\mathbf{M}\) is the returned matrix and \(\Re\{\mathbf{J}\}\) and \(\Im\{\mathbf{J}\}\) the real and imaginary components of \(\mathbf{J}\), respectively.

Parameters:
sionna.rt.utils.jones_vec_dot(u: mitsuba.Vector4f, v: mitsuba.Vector4f) → drjit.llvm.ad.Complex2f[source]#

Computes the dot product of two Jones vectors \(\mathbf{u}\) and \(\mathbf{v}\)

A Jones vector is assumed to be represented by a real-valued vector of four dimensions, obtained by concatenating its real and imaginary components. The returned array is complex-valued.

More precisely, the following formula is implemented:

\[\begin{split}\begin{multline} a = \mathbf{u}^\textsf{H} \mathbf{v}\\ = \left( \Re\{\mathbf{u}\}^\textsf{T} \Re\{\mathbf{v}\}\\ + \Im\{\mathbf{u}\}^\textsf{T} \Im\{\mathbf{v}\} \right)\\ + j\left( \Re\{\mathbf{u})^\textsf{T} \Im\{\mathbf{v}\}\\ - \Im\{\mathbf{u}\}^\textsf{T} \Re\{\mathbf{v}\} \right) \end{multline}\end{split}\]
Parameters:

Meshes#

sionna.rt.utils.load_mesh(fname: str, flip_normals: bool = True) → mitsuba.Mesh[source]#

Load a mesh from a file

This function loads a mesh from a given file and returns it as a Mitsuba mesh. The file must be in either PLY or OBJ format.

Parameters:

  • fname (str) – Filename of the mesh to be loaded

  • flip_normals (bool) – Whether to invert the normals of the mesh.

Returns:

Mitsuba mesh object representing the loaded mesh

sionna.rt.utils.transform_mesh(mesh: mitsuba.Mesh, translation: mitsuba.Point3f | None = None, rotation: mitsuba.Point3f | None = None, scale: mitsuba.Point3f | None = None)[source]#

In-place transformation of a mesh by applying translation, rotation, and scaling

The order of the transformations is as follows:

  1. Scaling

  2. Rotation

  3. Translation

Before applying the transformations, the mesh is centered.

Parameters:

  • mesh (mitsuba.Mesh) – Mesh to be edited. The mesh is modified in-place.

  • translation (mitsuba.Point3f | None) – Translation vector to apply

  • rotation (mitsuba.Point3f | None) – Rotation angles [rad] specified through three angles \((\alpha, \beta, \gamma)\) corresponding to a 3D rotation as defined in (3)

  • scale (mitsuba.Point3f | None) – Scaling vector for scaling along the x, y, and z axes

Miscellaneous#

sionna.rt.utils.complex_sqrt(x: drjit.llvm.ad.Complex2f) → drjit.llvm.ad.Complex2f[source]#

Computes the square root of a complex number \(x\)

The following formula is implemented to compute the square roots of complex numbers: https://en.wikipedia.org/wiki/Square_root#Algebraic_formula

Parameters:

x (drjit.llvm.ad.Complex2f) – Complex number

sionna.rt.utils.dbm_to_watt(x: drjit.llvm.ad.Float) → drjit.llvm.ad.Float[source]#

Converts dBm to Watt

Implements the following formula:

\[P_W = 10^{\frac{P_{dBm}-30}{10}}\]
Parameters:

x (drjit.llvm.ad.Float) – Power [dBm]

sionna.rt.utils.isclose(a: drjit.llvm.ad.Float, b: drjit.llvm.ad.Float, rtol: drjit.llvm.ad.Float = 1e-05, atol: drjit.llvm.ad.Float = 1e-08) → drjit.llvm.ad.Bool[source]#

Returns an array of boolean in which an element is set to True if the corresponding entries in a and b are equal within a tolerance

More precisely, this function returns True for the \(i^{th}\) element if:

\[|\texttt{a}[i] - \texttt{b}[i]| < \texttt{atol} + \texttt{rtol} \cdot \texttt{b}[i]\]
Parameters:
sionna.rt.utils.log10(x: drjit.llvm.ad.Float) → drjit.llvm.ad.Float[source]#

Evaluates the base-10 logarithm

Parameters:

x (drjit.llvm.ad.Float) – Input value

sionna.rt.utils.sigmoid(x: drjit.llvm.ad.Float) → drjit.llvm.ad.Float[source]#

Evaluates the sigmoid of x

Parameters:

x (drjit.llvm.ad.Float) – Input value

sionna.rt.utils.sinc(x: drjit.llvm.ad.Float) → drjit.llvm.ad.Float[source]#

Evaluates the normalized sinc function

The sinc function is defined as \(\sin(\pi x)/(\pi x)\) for any \(x \neq 0\) and equals \(0\) for \(x=0\).

Parameters:

x (drjit.llvm.ad.Float)

sionna.rt.utils.subcarrier_frequencies(num_subcarriers: int, subcarrier_spacing: float) → drjit.llvm.ad.Float[source]#

Compute the baseband frequencies of num_subcarrier subcarriers spaced by subcarrier_spacing, i.e.,

>>> # If num_subcarrier is even:
>>> frequencies = [-num_subcarrier/2, ..., 0, ..., num_subcarrier/2-1] * subcarrier_spacing
>>>
>>> # If num_subcarrier is odd:
>>> frequencies = [-(num_subcarrier-1)/2, ..., 0, ..., (num_subcarrier-1)/2] * subcarrier_spacing
Parameters:

  • num_subcarriers (int) – Number of subcarriers

  • subcarrier_spacing (float) – Subcarrier spacing [Hz]

Returns:

Baseband frequencies of subcarriers

sionna.rt.utils.watt_to_dbm(x: drjit.llvm.ad.Float) → drjit.llvm.ad.Float[source]#

Converts Watt to dBm

Implements the following formula:

\[P_{dBm} = 30 + 10 \log_{10}(P_W)\]
Parameters:

x (drjit.llvm.ad.Float) – Power [W]

Ray tracing#

sionna.rt.utils.fibonacci_lattice(num_points: int) → mitsuba.Point2f[source]#

Generates a Fibonacci lattice of size num_points on the unit square \([0, 1] \times [0, 1]\)

Parameters:

num_points (int) – Size of the lattice

sionna.rt.utils.spawn_ray_from_sources(lattice: Callable[[int], mitsuba.Point2f], samples_per_src: int, src_positions: mitsuba.Point3f) → mitsuba.Ray3f[source]#

Spawns samples_per_src rays for each source at the positions specified by src_positions, oriented in the directions defined by the lattice

The spawned rays are ordered samples-first.

Parameters:

  • lattice (Callable[[int], mitsuba.Point2f]) – Callable that generates the lattice used as directions for the rays

  • samples_per_src (int) – Number of rays per source to spawn

  • src_positions (mitsuba.Point3f) – Positions of the sources

sionna.rt.utils.offset_p(p: mitsuba.Point3f, d: mitsuba.Vector3f, n: mitsuba.Vector3f) → mitsuba.Point3f[source]#

Adds a small offset to \(\mathbf{p}\) along \(\mathbf{n}\) such that \(\mathbf{n}^{\textsf{T}} \mathbf{d} \gt 0\)

More precisely, this function returns \(\mathbf{o}\) such that:

\[\mathbf{o} = \mathbf{p} + \epsilon\left(1 + \max{\left\{|p_x|,|p_y|,|p_z|\right\}}\right)\texttt{sign}(\mathbf{d} \cdot \mathbf{n})\mathbf{n}\]

where \(\epsilon\) depends on the numerical precision and \(\mathbf{p} = (p_x,p_y,p_z)\).

Parameters:
sionna.rt.utils.spawn_ray_towards(p: mitsuba.Point3f, t: mitsuba.Point3f, n: mitsuba.Vector3f | None = None) → mitsuba.Ray3f[source]#

Spawns a ray with infinite length from \(\mathbf{p}\) toward \(\mathbf{t}\)

If \(\mathbf{n}\) is not None, then a small offset is added to \(\mathbf{p}\) along \(\mathbf{n}\) in the direction of \(\mathbf{t}\).

Parameters:
sionna.rt.utils.spawn_ray_to(p: mitsuba.Point3f, t: mitsuba.Point3f, n: mitsuba.Vector3f | None = None) → mitsuba.Ray3f[source]#

Spawns a finite ray from \(\mathbf{p}\) to \(\mathbf{t}\)

The length of the ray is set to \(\|\mathbf{p} - \mathbf{t}\|\).

If \(\mathbf{n}\) is not None, then a small offset is added to \(\mathbf{p}\) along \(\mathbf{n}\) in the direction of \(\mathbf{t}\).

Parameters: