Link Adaptation
Link adaptation (LA) is a crucial Layer-2 functionality, optimizing the performance of a single wireless link by dynamically adjusting the transmission parameters to match the current channel conditions.
The goal of LA is to:
Maximize the achieved throughput
While maintaining the block error rate (BLER) sufficiently small
Typically, the problem above is simplified to the following:
Maintain the BLER close to a predefined target value
where such target value is pre-designed to balance throughput and latency.
In this notebook, we illustrate how to use two state-of-the-art LA techniques available in Sionna SYS, namely:
Inner-loop link adaptation (ILLA), which selects the highest modulation and coding scheme (MCS) guaranteeing a BLER not exceeding the predefined target value given the current channel conditions estimates;
Outer-loop link adaptation (OLLA), which exploits HARQ feedback to compensate for non-idealities in channel estimates.
We do so by leveraging the ray-traced channel samples generated by Sionna RT.
Imports
We start by importing Sionna and the relevant external libraries:
[1]:
import os
os.environ['TF_CPP_MIN_LOG_LEVEL'] = '3'
if os.getenv("CUDA_VISIBLE_DEVICES") is None:
gpu_num = 0 # Use "" to use the CPU
if gpu_num!="":
print(f'\nUsing GPU {gpu_num}\n')
else:
print('\nUsing CPU\n')
os.environ["CUDA_VISIBLE_DEVICES"] = f"{gpu_num}"
# Import Sionna
try:
import sionna.sys
import sionna.rt
except ImportError as e:
import sys
if 'google.colab' in sys.modules:
# Install Sionna in Google Colab
print("Installing Sionna and restarting the runtime. Please run the cell again.")
os.system("pip install sionna")
os.kill(os.getpid(), 5)
else:
raise e
# Configure the notebook to use only a single GPU and allocate only as much memory as needed
# For more details, see https://www.tensorflow.org/guide/gpu
import tensorflow as tf
tf.get_logger().setLevel('ERROR')
gpus = tf.config.list_physical_devices('GPU')
if gpus:
try:
tf.config.experimental.set_memory_growth(gpus[0], True)
except RuntimeError as e:
print(e)
[2]:
# Additional external libraries
import matplotlib.pyplot as plt
import numpy as np
# Sionna components
from sionna.rt import load_scene, Transmitter, Receiver, PlanarArray, \
RadioMapSolver, PathSolver, subcarrier_frequencies, Camera
from sionna.phy import config
from sionna.phy.mimo import StreamManagement
from sionna.phy.ofdm import ResourceGrid, RZFPrecodedChannel, LMMSEPostEqualizationSINR
from sionna.phy.constants import BOLTZMANN_CONSTANT
from sionna.phy.utils import dbm_to_watt, lin_to_db, log2, db_to_lin
from sionna.sys import PHYAbstraction, InnerLoopLinkAdaptation, OuterLoopLinkAdaptation
from sionna.phy.nr.utils import decode_mcs_index
# Set random seed for reproducibility
sionna.phy.config.seed = 42
# Internal computational precision
sionna.phy.config.precision = 'single' # 'single' or 'double'
# Toggle to False to use the preview widget
# instead of rendering for scene visualization
no_preview = True
Simulation parameters
Note that we assume that the communication occurs in the downlink direction between a base station and a user terminal.
[3]:
# Number of slots to simulate
num_slots = 500
# BLER target value
bler_target = .1
# Time/frequency resource grid
carrier_frequency = 3.5
num_subcarriers = 1024
subcarrier_spacing = 30e3
num_ofdm_symbols = 13
# MCS table index
mcs_table_index = 1
# 1 base station is considered
num_bs = 1
# Number of antennas at the transmitter and receiver
num_bs_ant = 1
num_ut_ant = 1
# Number of streams per base station
num_streams_per_bs = num_ut_ant
# Base station transmit power
# Low power is sufficient thanks to the lack of interference
bs_power_dbm = 20 # [dBm]
bs_power_watt = dbm_to_watt(bs_power_dbm)
# Noise power per subcarrier
temperature = 294 # [K]
no = BOLTZMANN_CONSTANT * temperature * subcarrier_spacing
[4]:
# Transmit power is spread uniformly across subcarriers and streams
tx_power = np.ones(
shape=[1, num_bs, num_streams_per_bs, num_ofdm_symbols, num_subcarriers])
tx_power *= bs_power_watt / num_streams_per_bs / num_subcarriers
# (Trivial) stream management: 1 user and 1 base station
rx_tx_association = np.ones([1, num_bs])
stream_management = StreamManagement(rx_tx_association, num_streams_per_bs)
# OFDM resource grid
resource_grid = ResourceGrid(num_ofdm_symbols=num_ofdm_symbols,
fft_size=num_subcarriers,
subcarrier_spacing=subcarrier_spacing,
num_tx=num_bs,
num_streams_per_tx=num_streams_per_bs)
# Subcarrier frequencies
frequencies = subcarrier_frequencies(num_subcarriers=num_subcarriers,
subcarrier_spacing=subcarrier_spacing)
Generate the channel via Sionna RT
The user mobility is emulated by placing multiple receivers along a straight line, defined by its start and end points:
[5]:
# Start/end 3D position of the users
# You can try and change these values to see how the system behaves
ut_pos_start = np.array([-23, -40, 1.5])
ut_pos_end = np.array([-23, 50, 1.5])
# Base station position and look-at direction
bs_pos = np.array([32.5, 10.5, 23])
bs_look_at = np.array([22, -8, 0])
We load a scene to which users and base station are added.
[6]:
# Load a scene
scene = load_scene(sionna.rt.scene.simple_street_canyon)
# Set the scene parameters
scene.bandwidth = num_subcarriers * subcarrier_spacing
scene.tx_array = PlanarArray(
num_rows=1, num_cols=num_bs_ant, pattern="tr38901", polarization='V')
scene.rx_array = PlanarArray(
num_rows=1, num_cols=num_ut_ant, pattern="dipole", polarization='V')
# Add a transmitter to the scene
scene.add(Transmitter("bs", position=bs_pos, look_at=bs_look_at, power_dbm=bs_power_dbm, display_radius=3))
# Emulate moving users by placing multiple receivers along a straight line
step = (ut_pos_end - ut_pos_start) / (num_slots - 1)
# Add users at all future positions at once
for slot in range(num_slots):
scene.add(Receiver(f"ut{slot}", position=ut_pos_start + slot * step,
display_radius=1, color=[0, 0, 0]))
[7]:
# Configure Sionna RT
p_solver = PathSolver()
# Path solver: Compute propagation paths between the antennas of all
# transmitters and receivers in the scene using ray tracing
paths = p_solver(scene, max_depth=8, refraction=False)
# Transform to channel frequency response (CFR)
# [num_slots, num_rx_ant, num_tx, num_tx_ant, num_ofdm_symbols, num_subcarriers]
h_freq = paths.cfr(frequencies=frequencies,
sampling_frequency=1/resource_grid.ofdm_symbol_duration,
num_time_steps=resource_grid.num_ofdm_symbols,
out_type="tf")
From the visualization below, we observe that the user moves along a straight line, transitioning from non-line-of-sight (NLoS) to line-of-sight (LoS) and back to NLoS.
[8]:
# Compute the Radio Map for the scene and visualize it
rm_solver = RadioMapSolver()
rm = rm_solver(scene, max_depth=8, refraction=False,
cell_size=(1, 1), samples_per_tx=10000000)
if no_preview:
cam = Camera(position=[0, 0, 250],
orientation=np.array([0, np.pi/2, -np.pi/2]))
scene.render(camera=cam,
radio_map=rm,
rm_metric="sinr")
else:
scene.preview(radio_map=rm, rm_metric="sinr")
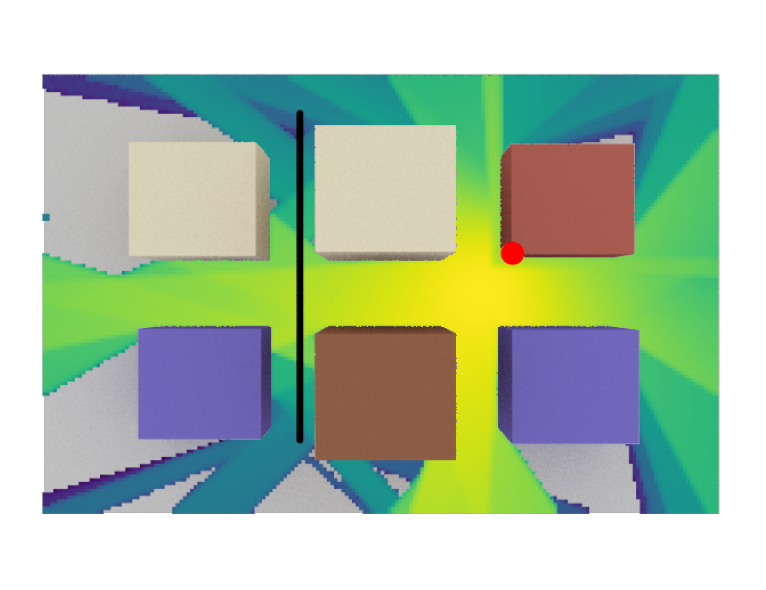
We will next show how link adaptation selects the MCS in response to the channel quality variations, while maintaining the BLER close to the target value.
The principles of link adaptation
In its general form, link adaptation (LA) accepts as input:
Previous HARQ feedback (ACK if the transmission was successful, else NACK);
Estimated channel conditions;
Scheduling decisions, to determine the number of coded bits;
and outputs the appropriate modulation and coding scheme (MCS), where
Modulation scheme determines the number of coded bits per symbol;
Coding scheme defines the coderate.
Note that the HARQ feedback value depends on the MCS index chosen for the last slot: the more aggressive the MCS, the higher the chance that the codeword is not correctly decoded, resulting in a negative (NACK) HARQ message.
In the following, we will create a layer-2 functionality that
Computes the SINR from the input channels;
Selects the MCS index via a general link adaptation algorithm (We will study different choices later on);
Generates the HARQ feedback via the PHYAbstraction functionality.
[9]:
# Initialize the PHYAbstraction object
phy_abs = PHYAbstraction()
# XLA compile for speed-ups
@tf.function(jit_compile=True)
def la_step(la,
h,
sinr_eff_feedback,
harq_feedback):
"""
Computes the SINR, select the MCS index, and generate the HARQ feedback for a
single step of the link adaptation algorithm.
"""
# Compute SINR
# Note that downlink is assumed
precoded_channel = RZFPrecodedChannel(resource_grid=resource_grid,
stream_management=stream_management)
h_eff = precoded_channel(h, tx_power=tx_power, alpha=no)
lmmse_posteq_sinr = LMMSEPostEqualizationSINR(resource_grid=resource_grid,
stream_management=stream_management)
# [batch_size, num_ofdm_symbols, num_effective_subcarriers, num_rx, num_streams_per_rx]
sinr = lmmse_posteq_sinr(h_eff, no=no)[0, ...]
# Number of allocated streams
num_allocated_re = tf.reduce_sum(
tf.cast(sinr > 0, tf.int32), axis=[-4, -3, -1])
# Select MCS index via ILLA
mcs_index = la(num_allocated_re=num_allocated_re,
sinr_eff=sinr_eff_feedback,
mcs_table_index=mcs_table_index,
mcs_category=1, # downlink
harq_feedback=harq_feedback)
# Send bits and collect HARQ feedback
_, harq_feedback, sinr_eff, *_ = phy_abs(
mcs_index,
sinr=sinr,
mcs_table_index=mcs_table_index,
mcs_category=1) # downlink
return mcs_index, harq_feedback, sinr_eff
Next, we write the function for simulating the process defined above over multiple time steps and recording the output.
Note that we offer the option of noisy channel quality estimates.
[10]:
def run(la,
noise_feedback=None):
"""
Calls the link adaptation and physical abstraction blocks over multiple time
steps and records the history of MCS indices and HARQ feedback.
Allows for the introduction of noise in the channel estimates.
"""
# Initialize history
mcs_index_hist = np.zeros((num_slots))
harq_feedback_hist = np.zeros((num_slots))
se_la_hist = np.zeros((num_slots))
se_shannon_hist = np.zeros((num_slots))
sinr_eff_db_hist = np.zeros((num_slots))
# Initialize HARQ feedback to -1 (missing)
harq_feedback = - tf.cast(1, dtype=tf.int32)
# Initialize SINR feedback
sinr_eff_db_true = tf.cast([0], tf.float32)
for i in range(num_slots):
# [num_rx_ant, num_tx, num_tx_ant, num_ofdm_symbols, num_subcarriers]
h = h_freq[i, ...]
h = h[tf.newaxis, tf.newaxis, ...]
# Noisy channel estimate
if noise_feedback is not None:
sinr_eff_db_feedback = sinr_eff_db_true + noise_feedback[i]
else:
sinr_eff_db_feedback = sinr_eff_db_true
# Link Adaptation
mcs_index, harq_feedback, sinr_eff_true = la_step(
la,
h,
sinr_eff_feedback=db_to_lin(sinr_eff_db_feedback),
harq_feedback=harq_feedback)
sinr_eff_db_true = lin_to_db(sinr_eff_true)
# Spectral efficiency
mod_order, coderate = decode_mcs_index(
mcs_index,
table_index=mcs_table_index,
is_pusch=False)
if harq_feedback == 1:
se_la = tf.cast(mod_order, coderate.dtype) * coderate
else:
se_la = tf.cast([0], tf.int32)
# Shannon capacity
se_shannon = log2(1 + sinr_eff_true)
# Record history
mcs_index_hist[i] = mcs_index[0].numpy()
harq_feedback_hist[i] = harq_feedback[0].numpy()
se_la_hist[i] = se_la[0].numpy()
se_shannon_hist[i] = se_shannon[0].numpy()
sinr_eff_db_hist[i] = sinr_eff_db_true[0].numpy()
return sinr_eff_db_hist, mcs_index_hist, harq_feedback_hist, \
se_la_hist, se_shannon_hist
Inner-Loop Link Adaptation (ILLA)
The simplest form of link adaptation is the so-called inner-loop link adaptation (ILLA), which selects the highest MCS whose corresponding BLER does not exceed a predefined BLER target.
Importantly, ILLA does not rely on any feedback loop, such as HARQ feedback, and fully relies on the estimated channel conditions.
Perfect channel estimate
Next, we will run ILLA over the ray-traced scenario defined at the beginning of the notebook.
[11]:
# Initialize the ILLA object
illa = InnerLoopLinkAdaptation(phy_abs,
bler_target=bler_target)
# Simulate ILLA over multiple time steps
sinr_eff_db_hist, mcs_illa_ideal, harq_illa_ideal, se_illa_ideal, se_shannon = \
run(illa)
We can now visualize the results:
[12]:
def plot(sinr_eff_db_hist, se_la_hist, se_shannon_hist, harq_feedback_hist,
noise_feedback=None, fig=None, label=None, linestyle='-'):
is_first_plot = fig is None
if fig is not None:
axs = fig.get_axes()
else:
fig, axs = plt.subplots(3, 1, sharex='col', sharey='row',
figsize=(5, 9))
if is_first_plot:
for ax in axs.flat:
ax.yaxis.set_tick_params(labelleft=True)
ax.xaxis.set_tick_params(labelbottom=True)
ax.grid()
if is_first_plot:
axs[0].plot(sinr_eff_db_hist, label='true')
if noise_feedback is not None:
axs[0].plot(sinr_eff_db_hist + noise_feedback,
':', label='noisy feedback')
axs[0].set_ylabel('SINR [dB]')
axs[0].set_xlabel('Slot')
axs[0].legend()
axs[1].plot(se_la_hist[:], linestyle=linestyle, label=label)
if is_first_plot:
axs[1].plot(se_shannon_hist, '--k', label='Shannon capacity')
axs[1].set_ylabel('Spectral efficiency [bps/Hz]')
axs[1].set_xlabel('Slot')
axs[1].legend()
if is_first_plot:
axs[2].plot([0, num_slots - 1], [bler_target]
* 2, '--k', label='BLER target')
axs[2].plot(1 - np.cumsum(harq_feedback_hist) / np.arange(1, num_slots + 1),
linestyle=linestyle, label=label)
axs[2].set_ylabel('Achieved BLER')
axs[2].set_xlabel('Slot')
axs[2].legend()
fig.tight_layout()
return fig, axs
[13]:
fig, axs = plot(sinr_eff_db_hist, se_illa_ideal,
se_shannon, harq_illa_ideal, label='ILLA')
fig.suptitle('Inner Loop Link Adaptation (ILLA)\nPerfect channel estimate',
fontsize=16, y=1)
fig.tight_layout()
plt.show()
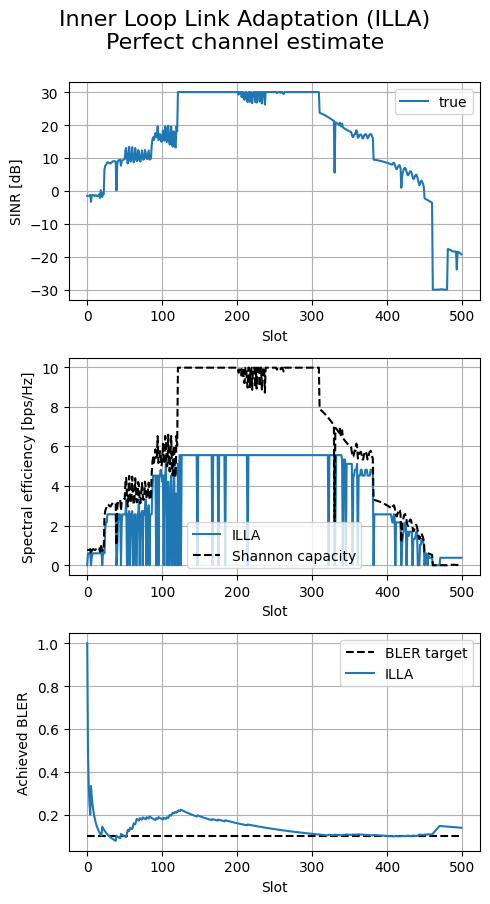
Note that the MCS evolution follows closely the one of the effective SINR: the higher the SINR, the higher the supported MCS index, hence the higher the spectral efficiency.
Moreover, the BLER is fairly close to the target.
However, the perfect channel estimate assumption is unrealistic: In real systems, the channel estimate is noisy and performed intermittently over time.
Imperfect channel estimation
We now address a more realistic scenario, where the channel estimates are noisy. We will observe that ILLA struggles in this scenario.
[14]:
noise_feedback_std = 1.5
noise_feedback = config.tf_rng.normal(
shape=[num_slots], dtype=tf.float32, stddev=noise_feedback_std)
# Simulate ILLA over multiple time steps
sinr_eff_db_hist, mcs_illa_noisy, harq_illa_noisy, se_illa_noisy, se_shannon = \
run(illa, noise_feedback=noise_feedback)
[15]:
fig, axs = plot(sinr_eff_db_hist, se_illa_noisy, se_shannon,
harq_illa_noisy, noise_feedback=noise_feedback, label='ILLA')
fig.suptitle('Inner Loop Link Adaptation (ILLA)\nImperfect channel estimate',
fontsize=16, y=1)
fig.tight_layout()
plt.show()
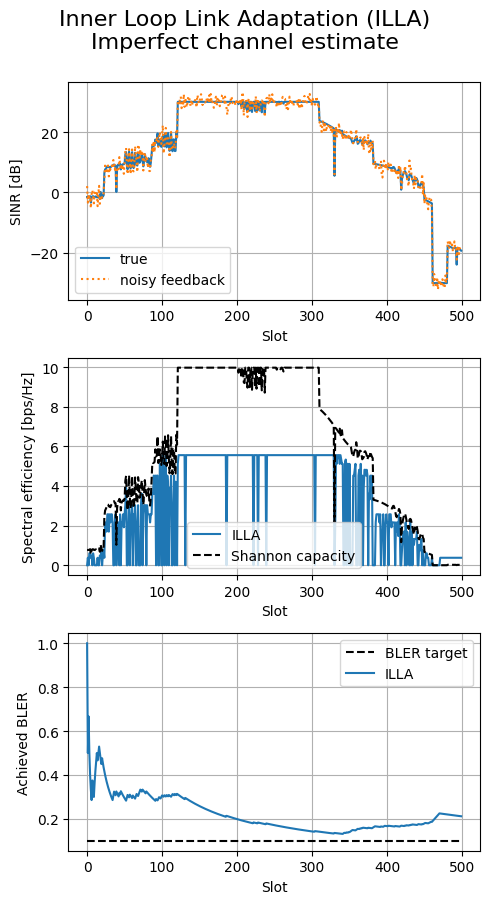
In the presence of noisy channel estimates, ILLA is no longer able to maintain the BLER close to the target value.
This is expected: ILLA fully relies on the provided estimates and does not even attempt to adjust its behavior based on the achieved BLER.
To this aim, a feedback-driven outer-loop is introduced in the following.
Outer-Loop Link Adaption (OLLA)
[16]:
# Instantiate an OLLA object
olla = OuterLoopLinkAdaptation(phy_abs,
num_ut=1,
bler_target=bler_target)
After instantiating the OLLA object, we can now run OLLA across multiple time steps on the ray-traced scenario defined at the beginning of the notebook.
[17]:
sinr_eff_db_hist, mcs_olla, harq_olla, se_olla, se_shannon = \
run(olla, noise_feedback=noise_feedback)
Finally, we visualize the results and compare them with ILLA.
[18]:
fig, axs = plot(sinr_eff_db_hist, se_illa_noisy, se_shannon, harq_illa_noisy,
noise_feedback=noise_feedback, label='ILLA')
fig.suptitle('Inner Loop Link Adaptation (ILLA)\nImperfect channel estimate',
fontsize=16, y=1)
fig, axs = plot(sinr_eff_db_hist, se_olla, se_shannon, harq_olla,
noise_feedback=noise_feedback, fig=fig, label='OLLA', linestyle='-.')
fig.suptitle('Imperfect CQI feedback',
fontsize=16, y=1)
fig.tight_layout()
plt.show()
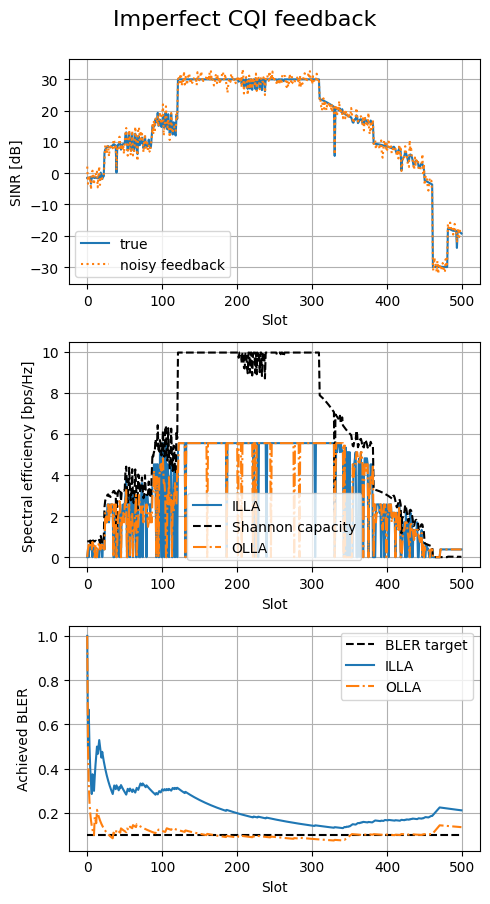
We observe that OLLA succeeds in maintaining the BLER close to the target value, although the channel estimates are noisy.
This occurs thanks to the closed-loop mechanism that adjusts the effective SINR according to the observed HARQ feedback.
Conclusions
References
[1] K. I. Pedersen, G. Monghal, I. Z. Kovacs, T. E. Kolding, A. Pokhariyal, F. Frederiksen, P. Mogensen. “Frequency domain scheduling for OFDMA with limited and noisy channel feedback.”,” 2007 IEEE 66th Vehicular Technology Conference, pp. 1792-1796, 2007.